Table of Contents
The Circles of Hell in Dante's Inferno
The Gist of Philosophical Thinkers
The following sections document the main ideas of some philosophers without too much elaboration. By no means should the list be considered either complete or exhaustive.
This section is fundamental and cited numerous times for various projects such as:
since this section is deemed to be the fundamental building-blocks for all the former.
Index
The Monty Hall Problem
The Monty Hall problem is a problem that can be explained mathematically but the problem exists initially due to human bias and that is why, according to us, the problem pertains more to the domain of philosophy rather than mathematics.
Here is the problem as expressed originally by Crag F. Whitaker and solved by Marilyn vos Savant's "Ask Marilyn" column in Parade magazine in 1990:
"Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice?"
The problem can easily be visualized using sets. The number of sets corresponds to the number of choices that a player has and the size of the set represents the probability of the car being there.
Initially, the probability of the car being behind one of the three doors is  , that is
, that is  where each individual probability
where each individual probability  represents a choice. Note that the player now has a ternary choice, incidentally represented here by three doors, each corresponding to three sets
represents a choice. Note that the player now has a ternary choice, incidentally represented here by three doors, each corresponding to three sets  ,
,  and
and  .
.
For completeness, at this point the system is valid because all the probabilities add up to 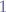 , that is the sum of probabilities for all sets
, that is the sum of probabilities for all sets  ,
,  and
and  is
is  .
.
![Equation $$
\begin{tikzpicture}
\draw[circle, thick, fill=pink, fill opacity=0.2] (0,0) circle (1cm) node {};
\node at (0,1.5) (A) {$P(A)= \{ \frac{1}{3} \}$};
\draw[circle, thick, fill=yellow, fill opacity=0.2] (2,0) circle (1cm) node {};
\node at (2,1.5) (B) {$P(B)= \{ \frac{1}{3} \}$};
\draw[circle, thick, fill=lime, fill opacity=0.2] (4,0) circle (1cm) node {};
\node at (4,1.5) (C) {$P(C)= \{ \frac{1}{3} \}$};
\end{tikzpicture}
$$](/lib/exe/fetch.php?media=wiki:latex:/img05f99b33362d34f558be7dc9ee191eaa.png)
The moment that the player makes their first choice and they pick a door, the system becomes a binary system where the probability of the picked door containing the car is set  with a probability of
with a probability of  while the probability that the car is behind "the other two doors" taken together is a new set
while the probability that the car is behind "the other two doors" taken together is a new set  , the union of sets
, the union of sets  and
and  with the set
with the set  now having a binary probability relative to
now having a binary probability relative to  of
of  .
.
For completeness, at this point the system is valid because all the probabilities add up to 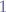 , that is, the sum of probabilities for all sets
, that is, the sum of probabilities for all sets  ,
,  is
is 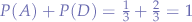 .
.
![Equation $$
\begin{tikzpicture}
\draw[circle, thick, fill=pink, fill opacity=0.2] (0,0) circle (1cm) node {};
\node at (0,1.5) (A) {$P(A) = \{ \frac{1}{3} \}$};
\draw[circle, thick, fill=yellow, fill opacity=0.2] (3,0) circle (2cm) node {};
\node at (3,2.5) (D) {$P(D) = \{ \frac{2}{3} \}$};
%\draw[circle, thick, fill=yellow, fill opacity=0.2] (4,0) circle (1cm) node {};
%\node at (4,-1.5) (F) {$P(F) = \{ \epsilon \}$};
\end{tikzpicture}
$$](/lib/exe/fetch.php?media=wiki:latex:/img2c17e2ab6fc10ab1b29f2775e58646d8.png)
From the point of view of the initial binary choice, the information does not matter and set  still holds a probability of
still holds a probability of  and set
and set  still holds a probability of
still holds a probability of  even if it is revealed that a subset of
even if it is revealed that a subset of  , here relabeled from
, here relabeled from  to
to  with an associated probability of
with an associated probability of  will not contain the car.
will not contain the car.
![Equation $$
\begin{tikzpicture}
\draw[circle, thick, fill=pink, fill opacity=0.2] (0,0) circle (1cm) node {};
\node at (0,1.5) (A) {$P(A) = \{ \frac{1}{3} \}$};
\draw[circle, thick, fill=yellow, fill opacity=0.2] (3,0) circle (2cm) node {};
\node at (3,2.5) (D) {$P(D) = \{ \frac{2}{3} \}$};
\draw[circle, thick, fill=lime, fill opacity=0.2] (3,-1) circle (1cm) node {};
\node at (3,.5) (F) {$P(F) = \{ \epsilon \}$};
\end{tikzpicture}
$$](/lib/exe/fetch.php?media=wiki:latex:/imgda5f4103958d318c6a2d7ec3220e8d1e.png)
It would be wrong to assume that  such that
such that  because the probability
because the probability  corresponding to "Door 3" was a calculation that was performed in a setting where there were three possible choices yet just by the TV host opening the door, the third choice "Door 3" does not exist anymore and a ternary choice system is now collapsed to a binary choice system such that the initial definition of the set
corresponding to "Door 3" was a calculation that was performed in a setting where there were three possible choices yet just by the TV host opening the door, the third choice "Door 3" does not exist anymore and a ternary choice system is now collapsed to a binary choice system such that the initial definition of the set  in the context of a binary choice system does not hold.
in the context of a binary choice system does not hold.
 was initially defined as "a choice" yet when the door is opened,
was initially defined as "a choice" yet when the door is opened,  is definitely not a choice anymore (so quite the opposite, not a choice!) such that it could not hold the exact same probability as
is definitely not a choice anymore (so quite the opposite, not a choice!) such that it could not hold the exact same probability as  . Instead some subset of
. Instead some subset of  , namely a set
, namely a set  is defined with the probability of the set
is defined with the probability of the set  to find a car being zero
to find a car being zero  is used instead. Thus, the probability of the car to be found in the set
is used instead. Thus, the probability of the car to be found in the set  is still
is still  because the the set
because the the set  does not change the probability
does not change the probability 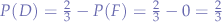 .
.
With that said, at this point the system is reduced to a binary choice where the player can only pick between the sets  or
or  .
.
![Equation $$
\begin{tikzpicture}
\draw[circle, thick, fill=pink, fill opacity=0.2] (0,0) circle (1cm) node {};
\node at (0,1.5) (A) {$P(A) = \{ \frac{1}{3} \}$};
\draw[circle, thick, fill=yellow, fill opacity=0.2] (3,0) circle (2cm) node {};
\node at (3,2.5) (D) {$P(D) = \{ \frac{2}{3} \}$};
\draw[circle, thick, fill=lime, fill opacity=0.2] (3,-1) circle (1cm) node {};
\node at (3,.5) (F) {$P(F) = \{ \epsilon \}$};
\end{tikzpicture}
$$](/lib/exe/fetch.php?media=wiki:latex:/imgda5f4103958d318c6a2d7ec3220e8d1e.png)
The only information that the player has is that set  has a probability of
has a probability of  , set
, set  has a probability of
has a probability of  and that some subset of
and that some subset of  namely
namely  with a probability of
with a probability of  that is uncannily in the same location in space and time as "Door 3" does not contain the car.
that is uncannily in the same location in space and time as "Door 3" does not contain the car.
Looking at the probabilities, the correct choice is to switch from the first door to the other door because the probability of the set  corresponding to the left-over door is greater than the probability of set
corresponding to the left-over door is greater than the probability of set  that corresponds to the first door.
that corresponds to the first door.
Perhaps with a connection to physics, in terms of logic, the Monty Hall problem relates to the two-slit experiment in the sense that the problem spans two different contexts. For the Monty Hall problem, the confusion how to calculate the probabilities is due to a system that switches contexts; namely, in the first stage, the system is a ternary-choice system and then, via the oracle, the system is collapsed to a binary-choice system. In changing the contexts, the same definitions do not apply anymore, such that the following probabilities cannot be computed the same way again - ie: a "possible" door is made to be a door that cannot be chosen for certain anymore such that in the new context, the problem must be approached in a different way. Similarly, the two-slit experiment concerning the duality of a photon as both a particle and a wave might be to the same fudging of contexts where the confusion arises because the initial definitions break when they were expected to hold. It's like being surprised that a tree feels hard when you knock your head against it even though the tree looked small from afar. Maybe, for the double slit experiment, the oracle is the player themselves which is much more confusing compared to the Monty Hall problem where the oracle is the TV show host.
Ironically, we leveraged the same trick and threw it back at the problem in order to create the illustrations by picking circles to represent the probabilities instead of boxes. One circle is sized 1 unit and the other circle is "double the size", yet by semantically performing "double the size - 1unit" the result is not "1 unit" due to the  constant that adds a residue which is used to ensure that subtracting the probability
constant that adds a residue which is used to ensure that subtracting the probability  from
from  does not end up with an area the same size as
does not end up with an area the same size as  .
.
The Sleeping Beauty Problem
The Sleeping Beauty problem is enunciated as follows:
"Some researchers are going to put you to sleep. During the two days that your sleep will last, they will briefly wake you up either once or twice, depending on the toss of a fair coin (Heads: once; Tails: twice). After each waking, they will put you to back to sleep with a drug that makes you forget the waking event. When you are first awakened, to what degree ought you believe that the outcome of the coin toss is Heads?"
by Adam Elga and the problem is based on a similar variation by Arnold Zuboff published in the paper "One Self: The Logic of Experience" in the 80s/90s.
We would illustrate the problem using a deterministic finite automaton (DFA) with state  being a temporary state that is not mentioned by Elga because it is not a terminating state.
being a temporary state that is not mentioned by Elga because it is not a terminating state.
![Equation $$
\begin{tikzpicture}[node distance = 2cm, scale=2]
\node[state, initial, ultra thick] (s0) {$\text{initial}$};
\node[state, right of=s0, ultra thick] (h1) {$H_{1}$};
\node[state, below of=h1] (t0) {$T_{0}$};
\node[state, right of=t0, ultra thick] (t1) {$T_{1}$};
\node[state, below right of=t0, ultra thick] (t2) {$T_{2}$};
\draw
(s0) edge[->] node{} (h1)
(s0) edge[->] node{} (t0)
(t0) edge[->] node{} (t1)
(t0) edge[->] node{} (t2);
\end{tikzpicture}
$$](/lib/exe/fetch.php?media=wiki:latex:/imgcf991e9c25e9c3dc716ba6121648b291.png)
Stances
Elga sustains that the answer to the problem is that the probability of "heads" being the toss is  , arguing that the states
, arguing that the states  ,
,  and
and  have equal probabilities such that the probability of all of them must add up to
have equal probabilities such that the probability of all of them must add up to 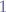 which means that the probability for sleeping beauty to be in either of the three states is equal to the probability of "heads" being tossed which is then
which means that the probability for sleeping beauty to be in either of the three states is equal to the probability of "heads" being tossed which is then  .
.
Halfer's position is a stance that states that the probability for heads is  and resulted from David Lewis responding to Elga's paper stating that without any memory there can be no additional inference that would allow sleeping beauty to make an educated choice between heads or tails such that the default 50 - 50 probability of
and resulted from David Lewis responding to Elga's paper stating that without any memory there can be no additional inference that would allow sleeping beauty to make an educated choice between heads or tails such that the default 50 - 50 probability of  would hold throughout the experiment.
would hold throughout the experiment.
The third most popular position is that the problem is ill-formulated, and this is the one that we subscribe to. It seems that the sleeping beauty problem, in its canonical format, offers either too much information for something things but too little information for others.
We would argue that Elga subsumed the notion of termination from continuations in the sense that all the chosen states that contribute to the probabilistic calculations are terminating states of the DFA, namely  ,
,  and
and  with
with  being a temporal state. This means that Elga removes the temporary state
being a temporal state. This means that Elga removes the temporary state  and then the number of possible outcomes from the point of view of termination is
and then the number of possible outcomes from the point of view of termination is  instead of all the possible states of the DFA that would be
instead of all the possible states of the DFA that would be  (and for whom the probability of heads would reduce to
(and for whom the probability of heads would reduce to  ).
).
Interesting Properties
The reason why, compared to others, we chose to use a DFA to illustrate the problem is due to the linearity of the experiment where the awakenings are used to demarcate time and the coin tosses imply that some events others follow from others. By adding termination as a parameter, which seems fairly important to the system, a Turing machine is obtained such that the whole system can just be approached like a linear-abstract machine.
Nevertheless, even if the problem is originally poorly formulated and appears to be ambiguous, depending on the states of the DFA, the following properties would hold that could convey some important information to sleeping beauty:
- iff. the oracle wakes up sleeping beauty and states that the game has terminated and the toss was heads, then sleeping beauty can assume that they are either at the first awakening
 or that they are at the second awakening and the preceding toss resulted in a tails toss at
or that they are at the second awakening and the preceding toss resulted in a tails toss at  ,
, - iff. the oracle wakes up sleeping beauty, states that the game has terminated and that the current toss was tails, then the player can only assume that they are in state
 ,
, - the third "temporary" state
 corresponds to the situation where sleeping beauty is awakened and the coin toss is tails and from then on her placement in time hinges upon the termination of the game; ie: iff. the oracle tells sleeping beauty that the game has terminated, then she is in
corresponds to the situation where sleeping beauty is awakened and the coin toss is tails and from then on her placement in time hinges upon the termination of the game; ie: iff. the oracle tells sleeping beauty that the game has terminated, then she is in  but if the oracle puts her back to sleep, she is in the temporary state
but if the oracle puts her back to sleep, she is in the temporary state 
The point is here that each property can be easily derived from the definitions and rules of the problem in an unambiguous way, compared to the probability of a coin-toss during some arbitrary wakeup that seems to really just follow the Occam's razor suggested by David Lewis "halfer position" because without any "memory" to carry over at least information about precedence, nor termination to add information about what follows, each individual state  or
or  or
or  or
or  are states that are perceived by sleeping beauty with no additional information to be derived from just being the next state in the automaton.
are states that are perceived by sleeping beauty with no additional information to be derived from just being the next state in the automaton.
It's like a set of equations with too many parameters yet too few relations to be solvable. Everyone that tackles this problem adds or removes some information thereby solving just a variation of the original; we added "termination" as a parameter to back up the problem with the solution from Elga but Elga changes the problem.
For the contact, copyright, license, warranty and privacy terms for the usage of this website please see the contact, license, privacy, copyright.




