Table of Contents
Vilfredo Pareto
- a neo-classic utilitarian, similar to the classic utilitarian Bentham,
- famous for the 80-20 rule, stating that 80% of outcomes are due to 20% of causes,
- initially applied the 80-20 rule to wealth redistribution by stating that 20% of the population controls 80% of the wealth,
- does not apply exclusively to economics, but rather has an impact on a wide-array of domains, where the rule expresses properties of statistical equilibrium that can apply to natural and organic distributions,
Pareto Efficiency
In classical utilitarianism, you want more of anything than less, but Pareto as a neo-classical utilitarian remarks that if you have a surplus of some type of goods but missing a different type of goods, the goods that are lacking are worth more than the goods that are there as surplus.
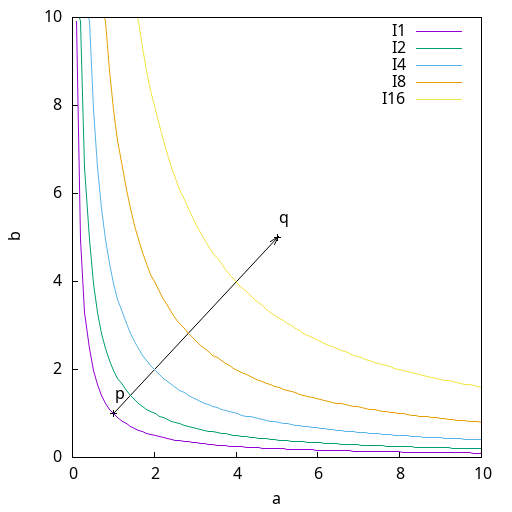
By representing two commodities (utilities), relative to each other with commodity a on the  axis and commodity
axis and commodity b on the  axis with the
axis with the  and
and  axis being quantified in terms of "amounts of", that is either "amounts of commodity a" on the
axis being quantified in terms of "amounts of", that is either "amounts of commodity a" on the  axis or "amounts of commodity b" on the
axis or "amounts of commodity b" on the  axis, the derived Pareto function
axis, the derived Pareto function 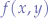 :
:

can be plotted separately in  multiples of
multiples of  , each plotted function representing a Pareto indifference curve for a given
, each plotted function representing a Pareto indifference curve for a given  value.
value.
It can be observed that, Pareto curves have a concave shape expressing the relativity of having more of either commodity "a" or commodity "b" where the concave shape illustrates the diminishing marginal returns when having "too much of a" relative to "too few of b" or "too much of b" relative to "too few of a".
As per Pareto definitions, each curve is also called an "indifference curve" where any point on a curve, say at 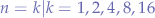 , that is decomposed and quantified in terms of commodity "a" and commodity "b", represents the same amount of happiness as any other point on the same curve
, that is decomposed and quantified in terms of commodity "a" and commodity "b", represents the same amount of happiness as any other point on the same curve  in terms of amounts of commodities "a" and "b".
in terms of amounts of commodities "a" and "b".
Pareto states that in order to reach a higher level of happiness, in terms of commodities "a" and "b", the only solution would be to jump onto a superior curve by increasing  . This is trivial to observe mathematically, given that any increase in
. This is trivial to observe mathematically, given that any increase in  will make any point on the superior curve be quantifiable superior in terms of amounts of "a" and "b", by looking at decomposing the points on
will make any point on the superior curve be quantifiable superior in terms of amounts of "a" and "b", by looking at decomposing the points on  and
and  axis and noticing that the same and more amounts can be obtained on the superior curve. In other words, the vector
axis and noticing that the same and more amounts can be obtained on the superior curve. In other words, the vector  represents the utility function analytically, that is the tendency to go up on the Pareto curve in order to reach a higher overall amount of commodities "a" and "b".
represents the utility function analytically, that is the tendency to go up on the Pareto curve in order to reach a higher overall amount of commodities "a" and "b".
The classical utilitarianism would attempt to quantify the exact amount of items needing to satisfy happiness but in Pareto terms of neo-classical utilitarianism, the scales are ordinal such the exact distance between two indifference curves  and
and 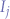 is not quantified and does not represent anything useful, only in a relative sense where, say
is not quantified and does not represent anything useful, only in a relative sense where, say  such that
such that  is preferable to
is preferable to 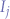 . This distinguishes the Pareto system as a system of statistical dynamics of markets by contrast to Bentham's utilitarianism that would have required a quantification of needs.
. This distinguishes the Pareto system as a system of statistical dynamics of markets by contrast to Bentham's utilitarianism that would have required a quantification of needs.
With neo-classical, as per Pareto, utilitarianism it is important to observe that the statistical distribution was designed to describe practical systems and to determine efficiency such that when the Pareto system is applied to human beings the distributions are agnostic in terms of humanitarianism (see Rousseau or Mill and the harm principle) leading to being perfectly acceptable for people/points to die off iff. they are unable to transact anything of value on the market. Nevertheless, as long as it is retained that Pareto efficiency is a theoretical curve describing the ideal state of market transactions, the Rawlsian distributive systems pertain more to human beings and should not be confused with theoretical curves that can be also be applied to abstract systems (file size distribution in network traffic, hard disk drive error rates, oil reserves in oil fields, jobs assigned to supercomputers, price returns on individual stocks, sizes of sand particles, etc).
Origin of The Pareto Equations
As explained by Ulrich H. Kurzweg in a succinct document, Vilfredo Pareto proposed via statistical analysis that 80% of a country's wealth is held by about 20% of the people. He wrote that the departure takes place from an egalitarian state where each fraction of a population  owns the same fraction of wealth
owns the same fraction of wealth  , or, in other words:
, or, in other words:
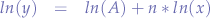
where:
Ais a constant.
If one requires that  varies with the same amount with
varies with the same amount with  , such then when
, such then when  ,
,  , or
, or  ,
,  , etc, then by induction the formula reduces to the law of powers:
, etc, then by induction the formula reduces to the law of powers:

Deriving the last equation by  and by
and by  :
:
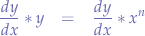
the formula can be reduced further to the Parto function 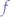 :
:
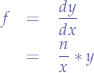
such that 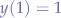
Then, plotting the Pareto function 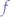 :
:
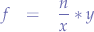
for a range of  values results in multiple Pareto curves.
values results in multiple Pareto curves.
Considering a wealth to population distribution where  represents fraction of wealth and
represents fraction of wealth and  represents fraction of the population, the following observations can be made as per Pareto dynamics:
represents fraction of the population, the following observations can be made as per Pareto dynamics:
- iff. the population remains discrete and the wealth increases to infinity, infinite utility can be obtained (theoretically),
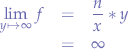
- iff. the wealth remains discrete and the population increase to infinity, then no utility can be achieved,
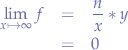
and the cases where  being the egalitarian state where
being the egalitarian state where  and
and  divide in equal shares or the totalitarian state where
divide in equal shares or the totalitarian state where  where the wealth is held by one single person.
where the wealth is held by one single person.
For instance, looking at the the wealth distribution of the U.S.A., the closest Pareto curve when looking at the ratio of the fraction of wealth vs. the fraction of population holding the wealth, seems to be at  for the 10% of the population controlling 71% of the wealth.
for the 10% of the population controlling 71% of the wealth.
Knowing the closest Pareto curve, the Gini coefficient  as defined as:
as defined as:
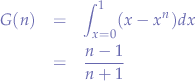
can be used to check whether the system is egalitarian or totalitarian by substituting the closest Pareto curve, in this case,  .
.
That is, numerically:

where a value of  would have represented perfect equality and
would have represented perfect equality and  would have represented perfect totalitarianism (that is, when
would have represented perfect totalitarianism (that is, when  , then
, then  ).
).
For the contact, copyright, license, warranty and privacy terms for the usage of this website please see the contact, license, privacy, copyright.