Table of Contents
About
Corrade uses key-value pairs as the first order structure and CSV as a second-order sub-structure whenever Corrade has to return data. In order to interpret the data, there are some invariants that Corrade maintains and on which the various data processing functions rely on.
Key-Value Pairs (Structure)
Corrade returns key-value pairs such as:
key=value
for all feedback.
For instance, Corrade could return the following:
dog=bark&cat=meow&food=coffee
The order in which the keys and values appear is undefined meaning that the previous example could also be written as:
cat=meow&dog=bark&food=coffee
or even:
food=coffee&dog=bark&cat=meow
as long as the following invariants are preserved:
- The keys (
food,dog,cat) are unique. - The relative mappings (
food->coffee,dog->bark,cat->meow) are maintained. - The ordering of key and value tuples can be arbitrary.
The Wizardry and Steamworks key-value functions are able to extract keys and values following the rules.
Comma Separated Values (CSV) (Substructure)
The second substructure that Corrade returns for all data processing and retrieval commands is represented as Comma Separated Values (CSV). For instance, were we to send the command to Corrade:
range=16&command=getprimitivesdata&data=Name,ID&entity=range&callback=http://...
the requested data:
data=Name,ID
would possibly return something like:
ID,ebb103f5-c54f-b821-c307-0b972a110291,Name,"TIKI TATTOO - 3D Light Palm Tree tall straight LIGHT- mesh",Name,"-FelineS City - Shop XS #31",ID,976e622e-5025-038f-b58d-9c6c9be5be6b,Name,":Fanatik Architecture: LONDON Straight B",ID,e844443c-232a-4532-68cd-75798c224b88
In contexts where data-commands are used (command names suffixed with the data string), Corrade returns a CSV list of predicates employing the terminology As by Bs by Cs which signifies in practice a list of the shape:
A, 10, g, B, 20, e, C, 5
where the value of each predicate immediately follows the predicate. Even though the data format is still CSV, the meaning of traditional "rows and columns" is in fact implicit within the syntax of the CSV used by Corrade. In other words, since data can only be transmitted linearly as strings without being able to supply "files", the columns and rows appear interrelated within the syntax.
For instance, the data string above:
A, 10, g, B, 20, e, C, 5
is identical in meaning to the "CSV table with headers":
| A | B | C |
|---|---|---|
| 10 | 20 | 5 |
| g | e |
There are two ways to linearize a table:
- serialize the table column by column
- serialize the table row by row
In terms of required complexity the two methods are identical and the choice of serializing column by column is a Corrade design choice.
Formally a CSV data string returned by Corrade, can be expressed as a double union series of keys  and values
and values 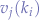 :
:
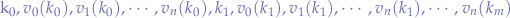
where the set of keys can be expressed as a union of all individual keys:
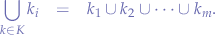
and the values as the union of all individual values corresponding to each key:
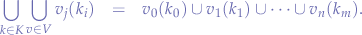
Locating a particular set of values hinges on locating the key within the series since iff.  is known then the set of values
is known then the set of values 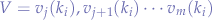 can be determined by extracting the values corresponding to
can be determined by extracting the values corresponding to  .
.
It is important to note that the cardinality of a set of values 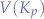 is not necessarily equal to the cardinality of the set of values for a different key
is not necessarily equal to the cardinality of the set of values for a different key 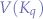 or, in mathemtical terms,
or, in mathemtical terms,  . In other words, if a key,
. In other words, if a key,  corresponds to a set of
corresponds to a set of  values
values 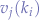 ,
, 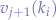 and
and 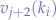 then any other key in the sequence
then any other key in the sequence 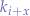 will not necessarily have
will not necessarily have  corresponding values
corresponding values 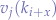 ,
, 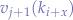 and
and 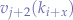 .
.
It would have been possible to pad all corresponding missing cells in order to account for the missing values, as we will see later on for commands prefixed by batch and suffixed by data, but since Corrade reads tables column by column the padding would inflate the amount of data too much. Ultimately, both design decisions (the decision to serialize tables column by column and the decision to not pad the data with empty cells) hinge on the fact that commmands prefixed by batch and suffixed by data are convenient meta-commands that could just as well be substituted by a simple loop querying the data for all items in the batch. In other words, the decision to serialize tables column by column implies that missing data for commands prefixed by batch and suffixed by data will not be padded in order to not increase the output unacceptably when column lengths are unbalanced.
For all commands prefixed by batch and suffixed by data, the following pattern might be observed that is different to the previously explained:
A, 10, g, B, 20, e, C, 5, A, 2, o, B, 46, c, C, 3
which means nothing more than two different tables - why? Because batch-prefixed and data-suffixed commands query multiple objects but of the same type such that for each object a different table is generated to correspond to the data queried by the requested data parameter of the command:
| A | B | C |
|---|---|---|
| 10 | 20 | 5 |
| g | e |
| A | B | C |
|---|---|---|
| 2 | 46 | 3 |
| o | c |
Identical to the previous method, the columns are read out in sequence yielding the CSV string A, 10, g, B, 20, e, C, 5, A, 2, o, B, 46, c, C, 3.
By contrast to the previous statement on set cardinality, the order of a table in the case of batch-prefixed commands is equal to the order for all tables of the objects being queried - this happens as a consequence of retrieving the value of a variable which can be empty rather than being a design decision. For instance, if the hair color is queried for a set of avatars and one of the avatars is not wearing hair, then Corrade will return an empty CSV cell as the placeholder for the missing hair. Counter-intuitive perhaps, even to experienced programmers but the entities "an empty value" and "the lack of a value" are conceptually different - you will notice throughout the documentation that "the empty string" is a valid value for a variable of type string and not just  as mathematics (ie, Hoare logic) would hope to idealistically achieve. Even in cases where variables are not initialized to default values, ie, in C programming, an allocated pointer yet uninitialized pointer still references "something" even if it is memory garbage that is, at best, "unuseful" in meaning. Becoming more intuitive now, perhaps even to experienced programmers, but this is the reason why programmers "conveniently" initialize variables to
as mathematics (ie, Hoare logic) would hope to idealistically achieve. Even in cases where variables are not initialized to default values, ie, in C programming, an allocated pointer yet uninitialized pointer still references "something" even if it is memory garbage that is, at best, "unuseful" in meaning. Becoming more intuitive now, perhaps even to experienced programmers, but this is the reason why programmers "conveniently" initialize variables to null - that is, as a marker for "there be nothing useful in this variable" since checking against null is possible compared to checking against "is this garbage?" (which does not even exist since to the computer all memory, useful or not, is meaningfully to the computer, indistinguishable garbage).
The math in this situation does not change but only blows up to include the notion of separate tables:
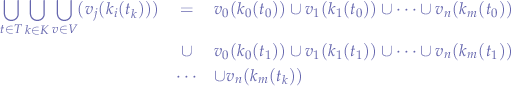
As with singular tables for single objects, perhaps the most important is the order of application of the functions 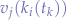 that gives away the order to operations that must be performed programmatically: find the desired table (object)
that gives away the order to operations that must be performed programmatically: find the desired table (object) 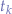 , obtain the desired key
, obtain the desired key  and then obtain the value(s)
and then obtain the value(s) 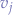 . In practice, we know that
. In practice, we know that data-suffixed commands query objects of the same type batch-prefixed commands indicate and a specific number of objects and we know that the data parameter specifies a fixed-set of keys to query such the table, key and values can be obtained in order.
For example, the following string would be obtained by issuing a pre-batch and post-data suffixed Corrade command, querying  specified objects (let that be,
specified objects (let that be,  in-world avatars, in order) and with the data parameter set to the CSV list of parameters and corresponding lengths
in-world avatars, in order) and with the data parameter set to the CSV list of parameters and corresponding lengths 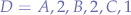 (let that be, the
(let that be, the name of the creator of lenses of their glasses, the name of the creator of their earrings and the age of the in-world avatar, in order) abstractly:
A, 10, g, B, 20, e, C, 5, A, 2, o, B, 46, c, C, 3, A, 3, p, B, 2, v, C, 19, A, 40, o, B, 3, i, C, 1
Following the example, suppose that we wanted to find out the age of the  nd avatar then the operations that must be performed, in order are, abstractly:
nd avatar then the operations that must be performed, in order are, abstractly:
- find the table,
- find the key,
- find the value
and concretely:
- find the avatar,
- find the
agekey, - find the value of the
agekey
Knowing that exactly  in-world avatars were queried by the
in-world avatars were queried by the batch-prefixed command:
- the string is split into
 equal parts, each part representing an avatar (remember the discussion on set cardinality and that the order of tables is equal across all avatars):
equal parts, each part representing an avatar (remember the discussion on set cardinality and that the order of tables is equal across all avatars):
A, 10, g, B, 20, e, C, 5 A, 2, o, B, 46, c, C, 3 A, 3, p, B, 2, v, C, 19 A, 40, o, B, 3, i, C, 1
- we said that the
 nd avatar is relevant to us such that the list of tables reduces to:
nd avatar is relevant to us such that the list of tables reduces to:
A, 2, o, B, 46, c, C, 3
- we said that the
ageis desired and knowing that the CSV list passed to thedataparameter is a fixed set of keys by the amount of values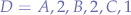 representing, in order,
representing, in order, first name,last name,agethen the key we are looking for isCsuch that the list reduces to:
C, 3
- dereferencing the key
C, theage, by looking up the length of the value for the key in
in  , the
, the ageis obtained:
3
For completeness sake, the command for the former inference would have the following form (where the avatars, authentication tokens, elements in the data list and callback URL, are all fictive):
command=batchgetavatarappearancedata & group=GROUP & password=PASSWORD & avatars="Fuzzy Resident","Ana Resident",3b3806df-c246-4ff4-81fb-789e623ce7cd,ebd4d1a2-8b02-4474-8e9f-f750c5365484 & data="creator of lenses","creator of earrings",age & callback=URL
Even thought the former might seem complicated, the operations performed upon receiving the fictive string to the callback URL:
A, 10, g, B, 20, e, C, 5, A, 2, o, B, 46, c, C, 3, A, 3, p, B, 2, v, C, 19, A, 40, o, B, 3, i, C, 1
in order to obtain the age are straightforward, abstractly:

and concretely in LSL:
// The number of objects queried. integer C = 4; // The desired object (table). integer O = 2; // The desired key to retrieve the values for. string K = "C"; // The data keys being queried and their known value lengths. list D = [ "A", 2, "B", 2, "C", 1 ]; string callback="data=A,10,g,B,20,e,C,5,A,2,o,B,46,c,C,3,A,3,p,B,2,v,C,19,A,40,o,B,3,i,C,1"; string data = wasKeyValueGet("data", callback); list l = wasCSVToList(data); integer n = llGetListLength(l) / C; l = llList2List(l, (O - 1)*n, (O - 1)*n + n - 1); integer x = 0; integer j; for(j=0; j < llGetListLength(D); j = j + 2) { x = x + llGetListLength(llList2List(D, j, j)) + llList2Integer(D, j + 1); } j = llListFindList(D, [K]); x = x - llGetListLength(llList2List(D, j, j)) - llList2Integer(D, j + 1); list v = llList2List(l, x+1, x + llList2Integer(D, j + 1)); return v;
The algorithm is complicated due to the fact that it uses a reduced number of operations (including functions) as well as being able to work under the assumption that keys are not distinguishable from values in data strings - which seems to be the case in the example at hand. In practice, the whole algorithm is more than often reduced to:

where after finding the table, both column headers (keys) and rows (values) are searched using llListFindList to find the index in the list of the key being sought after. Once the index is found, the list is split yet again right on the key and only the second half of the split is kept which represents the values for the key being sought after. The greatest advantage perhaps, is that a map of returned keys to returned value count does not have to be known.
As an example, querying a region for various parameters:
llInstantMessage(CORRADE, wasKeyValueEncode( [ "command", "getregiondata", "group", wasURLEscape(GROUP), "password", wasURLEscape(PASSWORD), // returns the last lag, the number of agents and the region flags "data", wasListToCSV( [ "Stats.LastLag", "Stats.Agents", "Flags" ] ), // sent to URL "callback", wasURLEscape(URL) ] ) );
would yield a data string along the lines of:
Stats.LastLag,228,Stats.Agents,2,Flags,AllowLandmark,AllowSetHome,AllowAccessOverride,NullLayer,ExternallyVisible,AllowDirectTeleport,AllowParcelChanges,AllowVoice
where the key Flags can just be linearly searched within the string since it does not appear anywhere else except as the implicit header for the region flags.
Note that some commands do not necessarily return data that is structured on columns but rather carry an exact specification that tells you exactly in which order the data will be returned. For instance, if you look on the getcurrentgroups command API page you will see that this command returns a CSV list of names by UUID. That means that Corrade will return something like the following:
"[Wizardry and Steamworks]:Support", "0026731c-e73b-4538-a98e-e46c0ed99fda", "Chocolate & Milk", "23208768-0f6b-421c-bead-7f1a434ca977"
In such a scenario, the order is meaningful: first the name of the group, then the UUID of the group such that you will never find an inversion such as:
"[Wizardry and Steamworks]:Support", "0026731c-e73b-4538-a98e-e46c0ed99fda", "23208768-0f6b-421c-bead-7f1a434ca977", "Chocolate & Milk"
In case you do, then you have found a bug in Corrade.
Sifting
Sometimes, in case the returned data is too large, the output will be truncated. http_request in LSL only supports up to 2KB of data and llSay, llOwnerSay, etc.. Are also capped to some amount. In such cases, your options are:
- Control Corrade from an external script and interface with Corrade's built-in HTTP server - that way, all the data can be passed back without any limitation.
- Use sifting to reduce the CSV returned by Corrade to some size that will work under the grid limits.
Index
For the contact, copyright, license, warranty and privacy terms for the usage of this website please see the contact, license, privacy, copyright.



