Table of Contents
Intersection Between a Segment and a Circle
![LaTeX
\begin{tikzpicture}
% grid
\draw[help lines] (-2,-2) grid (2,2);
% origin
\draw[red, line width=.1mm] (-0.1,-0.1) -- (0.1,0.1)
(0.1,-0.1) -- (-0.1,0.1);
\coordinate[label={[red]above left:$O(x_{0}, y_{0})$}] (O) at (0,0);
\coordinate (R) at (2,0);
% coord
\coordinate[label={[green]above left:$P_{1}(x_{1},y_{1})$}] (A) at (0,2);
\drawpoint{A}{.5mm}{black}
\coordinate[label={[blue]above right:$P_{2}(x_{2},y_{2})$}] (B) at (1.7,1);
\drawpoint{B}{.5mm}{black}
% lines
\draw (A) -- (B);
%radius
\draw[fill=orange,fill opacity=0.1] (O) -- (R);
%circle
\draw [black] (0,0) circle [radius=2];
%brace
\drawbrace{O}{R}{2mm}{orange}{$r$}{0}{-4mm}{mirror};
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/img9e6b54115dfed2a0df9ae22f40b44f3b.png)
We know that the circle equation is:

we also know that the equations for a segment  passing through two points
passing through two points  and
and 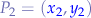 is:
is:
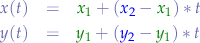
knowing that ![Math $t:\Re \mapsto [0,1]$](/lib/exe/fetch.php?media=wiki:latex:/imgfb1c12a35faf984323cbf0e0dc1ed134.png) , or, in other words,
, or, in other words, 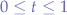 .
.
We substitute  for
for 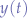 and
and  for
for 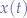 in the circle equation and obtain:
in the circle equation and obtain:

Now, we want to collect  , so we expand the left hand side and obtain:
, so we expand the left hand side and obtain:
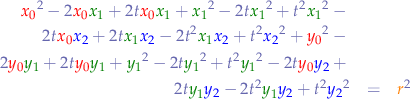
and collect  :
:
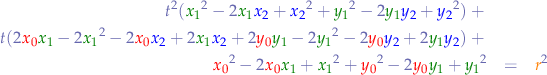
Passing  from the right-hand side to the left-hand side, we can rewrite the equation as:
from the right-hand side to the left-hand side, we can rewrite the equation as:
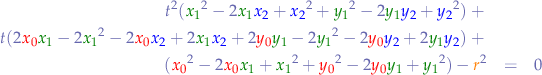
We can observe that if we name the bracketed expressions in the equation above  ,
,  respectively
respectively  :
:
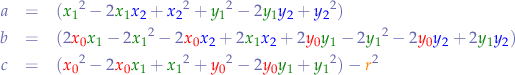
then we can reduce  ,
,  and
and  to:
to:
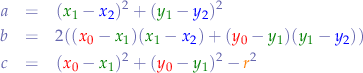
Looking at the equation now, we have a second-degree equation in  with
with  ,
,  and
and  :
:

The solutions for this equation are:

where we know  ,
,  ,
,  .
.
Now the discriminant is 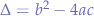 and depending on
and depending on  we have the cases:
we have the cases:
- in case
 then the line is tangent to the circle and intersects the circle in one single point.
then the line is tangent to the circle and intersects the circle in one single point. - in case
 then the line intersects the circle in two points.
then the line intersects the circle in two points. - in case
 then the line does not intersect the circle at all.
then the line does not intersect the circle at all.
By substituting 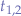 in the equation of the segment for
in the equation of the segment for 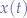 respectively
respectively 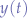 we obtain the point(s) of intersection between the segment
we obtain the point(s) of intersection between the segment  and the circle:
and the circle:
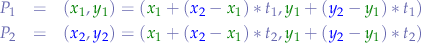
where we know 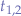 from the expression above.
from the expression above.
Implementation
The reason for simplifying  ,
,  and
and  , keeping
, keeping  as an relation between
as an relation between  ,
,  and
and  and by working symbolically we can reduce the number of operations that an implementation may have to do.
and by working symbolically we can reduce the number of operations that an implementation may have to do.
LSL
/////////////////////////////////////////////////////////////////////////// // Copyright (C) 2014 Wizardry and Steamworks - License: GNU GPLv3 // /////////////////////////////////////////////////////////////////////////// // given a circle with centre in C(x0x, c0y) and radius r and two points // p1 and p2 defining a line, the function returns the empty list if the // line p1p2 does not intersect the circle or a list containing two vectors // of the the intersection point(s). list wasLineIntersectCircle(float c0x, float c0y, float r, vector p1, vector p2) { // let dx = p1.x-p2.x // let dy = p1.y-p2.y float dx = p1.x - p2.x; float dy = p1.y - p2.y; // let dcx = c0x-p1.x // let dcy = c0y-p1.y float dcx = c0x - p1.x; float dcy = c0y - p1.y; float a = llPow(dx, 2) + llPow(dy, 2); float b = 2 * (dcx * dx + dcy * dy); float c = llPow(dcx, 2) + llPow(dcy, 2) - llPow(r, 2); // delta float delta = llPow(b, 2) - 4 * a * c; if (delta < 0) { // no intersection, no points return []; } float t1 = (-b + llSqrt(delta)) / (2 * a); float t2 = (-b - llSqrt(delta)) / (2 * a); return [ < p1.x - dx * t1, p1.y - dy * t1, 0 >, < p1.x - dx * t2, p1.y - dy * t2, 0 > ]; }
For the contact, copyright, license, warranty and privacy terms for the usage of this website please see the contact, license, privacy, copyright.



