About

Given that the activity priority table can be switched from "simple" to "advanced" in order to assign numeric priorities to activities, it is then possible to come up with various strategies depending on how the priorities are distributed. This section discusses some priorities and some of the challenges when picking a distribution function of the particular weights.

For context, the activity priority table can be used to assign weights to various activities. Just like the "simple mode" table, it is possible to untick the box for an activity, meaning then that the activity will not be performed at all. Otherwise, weights can be assigned that range between 1 representing the most important to 5 representing the least important.

It is important to realize that some activities can be performed ad infinitum because there is always work to do for that particular activity. For example, were the user to plant a bunch of evergreen trees allover the place, then in the summer every survivor with "Cut" enabled in the activity table will start felling. Similarly, farming along the lines of planting, represented by "Harvest" and "Plant", given a sizeable farm, will imply that there is always some planting or harvesting to be done. These activities where there is always lots of stuff to do frequently end up sucking up all the work time of a survivor such that with an ill-adjusted priority table, the survivor will end up not performing many tasks in favor of constantly grinding on the others. Here is a list of scenarios that are symptomatic of a bad distribution function for activity priorities:

Even though the player has a well-established base with plenty of cooking ingredients, nobody ever cooks and there is never any food with most of the survivors ending up eating "raw food" such as meat or berries.
No "Research", "Tailor" or "Craft" activity is ever carried out or crops are lost in favor of other meaningless activities that are not imperative.
More advanced items are never created.

Activity Weights Distribution Function Strategies

Depending on maintained patterns it is possible to set up an activity table that follows a particular strategy such that this section discusses a few strategies that seem useful. In order to implement these, the menu Mange→Activities has to be followed and the activity table has to be switched to "advanced mode" by clicking "simple priorities" until the numbers appear.

Ad-Hoc or On-Demand

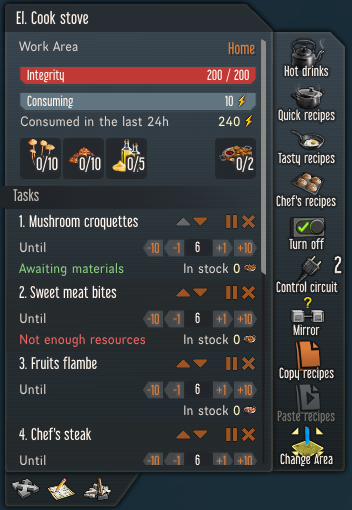
Concerning the scenario described above where no survivor is ever cooking anything, an on-demand strategy could be to set the activity priority for the survivor with the highest cooking skill to 1 (most preferred) in order to incentivize the survivor to cook. Given the game mechanics, it is very important to have someone with a high cooking skill dedicating their time to cook because survivors typically will eat in the morning and, given other duties, will typically just eat anything, whether raw or spuriously cooked. Having a dedicated cook, that is, a survivor with a high priority for the "Cook" activity is easily buffered by the availability of the ingredients and the desired count such that when there are no ingredients available, the survivor is free to complete the remaining other tasks. The following image is an overview of a cooking station setup for an on-demand strategy with an assigned cook.

The cooking menu includes the most difficult and highly valued recipes at the top by first selecting "Chef's recipes", selecting "Until" and then a desired stock number. In this case, there are 6 survivors in the game, such that the choice is taken to always have 6 of each recipes in stock.

On-demand also implies that various tasks that are seldom selected by survivors such as the "Craft", "Tailor" or "Assemble" activities will be given preferential treatment by setting the desired activities to the highest priority (1). For example, before "delivery drones", one of the main activities that survivors perform is to simply distribute goods to where they are needed, even if that requires crossing half the map between outposts. Unfortunately, the big loss here is in a scenario where, say, one of the survivors has a perfect intellect but wastes their time running around the map delivering goods when anyone else could perform the task - in the game mechanics, skill requirements imply precedence for some tasks, for example, every survivor can run around the map distributing goods but certain activities like "Research" require a higher intellect such that not every survivor will be able to carry out the "Research activity".

The losses are tremendous (more than linear) if activities are not compartmentalized, for example, during one of our playthroughs, the game ended up stagnating, the survivors progressively got ill, diseased and then died off although the base had all the necessary equipment. It turned out that due to no prioritization of the "Tailor" activity, all the survivors ended up using all the clothes and not creating any new clothes, such that they progressively got ill and then were even less motivated to perform other tasks due to having mental breakdowns, being depressed or dying from colds or pneumonia.

Efficiency

The most utilitarian strategy is to assign survivors to tasks that they are good at. The obtained effect is that the survivors will perform better in terms of efficiency, and, in the case that a survivor shows a particular interest for an activity (game modifier) will lean quicker than others. It is possible to also pragmatically derive an utilitarian strategy strategy given the following observations:

All survivor skills range from 0 to 10 where 0 is the least good at, respectively 10 represents very good at the given activity.
Some survivors have an "interested" game modifier for certain skills.
- Conversely, survivors have an "indifferent" game modifier for certain skills.
The activity priority table can have each activity set to "don't perform" or attributed a weight within the range of 1 (most preferred activity) to 5 (the least preferred activity).

Based on the above, it seems clear that for an utilitarian strategy, one would want to assign, say, a high priority (1) to activities for survivors with a high skill level for that given activity, respectively a low priority (5) to activities for survivors with a low skill level for that given activity. Mathematically this could be reduced to mapping the range $\[0,10\]$ , representing the range of skill proficiency to the range $\[5,1\]$ (or none), representing the range of priorities, such that a skill proficiency of 0, that is a survivor with very little skill for the given activity, will map to a priority or 5, the lowest priority.

First, using the formula for a linear map of values from one range into the other, the range $\[0,10\]$ is mapped into $\[1,5\]$ out of convenience:

$\begin{eqnarray*} \rho &=& 2 + ((5 - 2) * (s - 0)/(10 - 0)) \end{eqnarray*}$

where:

$\rho$ is the priority for a given activity and a given survivor,
$s$ is the skill of a given survivor for that particular activity

Note that the minimum priority value chosen is 2 even though the priorities are "don't do" and the range $\[1,5\]$ . This is intentional because a reservation is made for the priority 1 that is granted to any survivor that has the "interested" skill modifier for the given skill. In other words, in case a survivor is "interested" in a given skill, they are granted a priority of 1 for the activity matching that skill and regardless of their skill level. Otherwise, if the survivor does not have an "interested" modifier, then the priority is mapped based on their skill level. Furthermore, the previous formula will map the values switched around, such that the highest priority is assigned to the lowest skill and the obtained value will have to be rotated symmetrically in order to invert the range, using a simple range inversion formula:

$\begin{eqnarray*} \rho_{e} &=& 5 - (2 + ((5 - 2) * (s - 0)/(10 - 0))) + 2 \end{eqnarray*}$

where $\rho_{e}$ is the final priority value and the rest remains unchanged.

Note that the only variable that changes here over time is $s$ ; that is, the skill level of a survivor but it is also known that skill levels range in $\[1,10\]$ such that it is possible to create a lookup table from skill level to priority using the formula above. Using the Linux command line, the following one-liner does it nicely:

for s in 1 2 3 4 5 6 7 8 9 10; do 
    printf "$s -> %.2f\n" $(bc -l <<< "5 - (2 + ((5 - 2) * ($s - 0)/(10 - 0))) + 2")
done

obtaining:

1 -> 4.70
2 -> 4.40
3 -> 4.10
4 -> 3.80
5 -> 3.50
6 -> 3.20
7 -> 2.90
8 -> 2.60
9 -> 2.30
10 -> 2.00

where the separator is →, the left-column represents the skill-level column of a survivor and the right represents the priority to be set. Using the edge cases, a skill level of 0 (very bad) will imply a priority of 5.00 (least preferred) and conversely a skill level of 10 (excellent ) will imply a priority of 2.00 (very much preferred). Of course, the game is not that fine-grained and does not support floating-point numbers, and it is perhaps a matter of further strategizing based on whether the priority value should be round down or round up.

It is now much easier to open up the activity priority interface and look up the value that must be selected for a given activity and for a given survivor. The following image represents an instantiation of the formulas depending on the current skill level of every survivor for every activity.

The mapping for "Melody Adeyemi" seems pretty straight-forward with the highest priority given to the "Heal" activity followed by the activities that benefit from "Intellect" such as "Observe" and "Research" with the rest of the skills mapping using the formula like attributing a priority of 4 to a skill level of 6 for the "Farming" activity.

On the other hand, note that "Rakah Chad" has an "indifferent" modifier for the "Healing" skill and yet the priority value is 4 and not 5. The reason for that is that even if a skill has the "indifferent" modifier for a given activity, the survivor will still go ahead and perform the activity anyway, regardless whether they are "indifferent" or not. Not disabling activities for the "indifferent" modifier is highly important and is illustrated best here with "Rakah Chad" and the survivors impartiality to the "Heal" activity. Namely, if the activity would be disabled completely, then the survivor would gladly just sit around doing anything else while another survivor that needs to be healed is drying right next to them.

To sum up this strategy, the following rules are derived when setting the priorities in the activity table:

For a survivor and a skill marked "interested", the priority shall be set to 1,
For all other activities, the priority $\rho$ will be set using the formulas and will range in $[2,5]$

Balance Efficiency and Learning

Maybe, philosophically, learning is partially the opposite of efficiency, which would reflect well in a strategy where the survivors are meant to "catch up" on skills that they are not good at. This means that the strategy from the efficiency section will just have to be inverted, such that survivors that are bad at certain activities and hence skills, will end up doing those activities more in order to increase their skill. Conversely, the skills that a survivor is good at will be proportionally preferred less than skills that the survivor is bad at. However, skills that a survivor is interested in will be given preferential treatment.

Without further ado, remembering how the "efficiency" strategy was derived, the formula for $\rho_{e}$ , namely:

$\begin{eqnarray*} \rho_{e} &=& 2 + ((5 - 2) * (s - 0)/(10 - 0)) \end{eqnarray*}$

will be used to set priorities instead in the table.

The rules for setting the priorities do not change at all from the "efficiency" strategy.

Learning

As the complete opposite, the rule regarding the "interested" game skill modifier is disregarded in order to obtain a complete and total symmetric opposite of the mapping. In other words, $\rho_{e}$ changes into $\rho_{l}$ :

$\begin{eqnarray*} \rho_{l} &=& 1 + ((5 - 1) * (s - 0)/(10 - 0)) \end{eqnarray*}$

which now uses the full priority range $\[1, 5\]$ to map skills ranging in $\[0, 10\]$ .

The resulting strategy rules are the following:

Map any priority relative to the inverse skill level of a survivor for that activity using the formula given by $\rho_{l}$ .

The Slacker (Zero Fucks Given)

Let it be someone else's problem and whatever may be, may be!

$\begin{eqnarray*} \rho_{s} &=& \emptyset \end{eqnarray*}$

Or in other words, the priority for slacking $\rho_{s}$ is calculated as the empty set $\emptyset$ for all activities corresponding to the game mechanics where all the activities are disabled in the table such that every survivor just stands around doing nothing.

If winning the game is the purpose, then this is not a very good strategy given the other game mechanics.

Note there that setting the priority to either 1, where each survivor would lie that their skill is great at everything, or 5 where each survivor would lie that they are bad at everything, results in a game-relative semantic equivalent of outcomes. In other words, setting the priorities using either-or strategies, as in:

$\begin{eqnarray*} \rho &=& (1 + ((5 - 1) * (1 - 0)/(10 - 0))) \\ &\equiv& (1 + ((5 - 1) * (10 - 0)/(10 - 0))) \\ &=& \rho' \end{eqnarray*}$

would result in the same stagnation and festering of problems as described by the scenarios in the about section. In terms of game controls, this is the equivalent of ticking every box for every activity in the "Simple Priorities" mode.

Conclusions

Using the priority table in "Stranded: Alien Dawn" is crucial and can be the factor that determines the outcome of the entire expedition. The problem stems from the fact that, even though priorities for activities might be uniform or equal, the activities themselves imply a longer or shorter workout. For example, the difference is between felling an entire forest or creating a shirt, both of which are disproportionate to each other in terms of how much time is required to perform an activity, with felling an entire forest taking up much more time than sewing a shirt.

Furthermore, it is possible to play the game in different manners, for example, maxing out the skills of the survivors by making them perform tasks that they are bad at more frequently than tasks that they are good at whilst sacrificing efficiency and consistent results. Or, if reaching the end of the game faster is desired, going for "efficiency" instead of "learning" and using an utilitarian tactic to maximize outcomes based on the skill level of survivors for various activities.

Regardless of the "efficiency" or "learning" strategies, some on-demand exceptions can be made for crucial and yet trivial stuff that frequently gets ignored, namely activities such as "Cook" that only get applied on a personal-level given the game architecture. Survivors tend to eat in the morning, so they either cook themselves a dish, or, if the kitchen is busy, they will just eat raw food if it is enabled in their profile such that no advanced dish such as the "Chef's Special" is ever created as well as no stacks of cooked food.

Table of Contents