Table of Contents
Mean vs. Median
Suppose we have a set of values  , defined as:
, defined as:
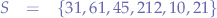
if we were to compute the arithmetic mean, we would obtain:
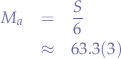
However, notice that this mean does not really look entirely "right" and that is due to the exceptional value  which drags the mean towards a very high value compared to the rest of the values in the set.
which drags the mean towards a very high value compared to the rest of the values in the set.
This is why, it is useful sometimes to compute the median which gives a more correct overview of the average of the set. In order to compute the median, we sort the set  in increasing order, thereby obtaining
in increasing order, thereby obtaining  :
:
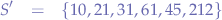
and calculate the arithmetic mean between the two values in the middle of the set:
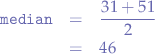
which gives us a median that is a better presentation of the middle of the original set  .
.
Standard Deviation
The standard deviation can be thought of measuring how far the data values are spread from the mean.
Let there be a random variable with mean value 
![Equations \begin{eqnarray*}
E[X] &=& \mu
\end{eqnarray*}](/lib/exe/fetch.php?media=wiki:latex:/imgc55eee2c5797d231b03bac33419cda4e.png)
where the operator  denotes the average or expected value of
denotes the average or expected value of  , then the standard deviation of
, then the standard deviation of  is the quantity:
is the quantity:
![Equations \begin{eqnarray*}
\sigma &=& \sqrt{E[X^{2}] - (E[X])^{2}}
\end{eqnarray*}](/lib/exe/fetch.php?media=wiki:latex:/img0c752f8e9b682eb38e1fb4daa134e4bb.png)
Example
Given a set  of measurements with the values:
of measurements with the values:
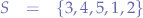
Calculate the arithmetic average  of the elements of the set:
of the elements of the set:
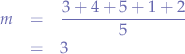
Calculate the difference squared between each element of the set  and the mean
and the mean  to obtain the set
to obtain the set  :
:
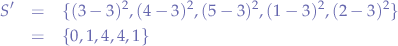
By summing up the elements of  (
(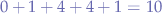 ) and then dividing by the number of elements minus one we obtain the variance
) and then dividing by the number of elements minus one we obtain the variance  :
:
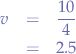
and the standard deviation  is the square root of the variance:
is the square root of the variance:
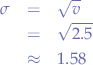
By subtracting and adding the standard deviation from the mean we found out the bounds between which most values are placed.
For the lower bound, we have:
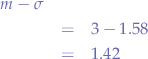
For the upper bound, we have:
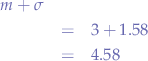
which means that most values are placed between 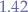 and
and 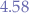 .
.
Chebyshev's Theorem
The fraction of any set of numbers lying within k-standard deviation of those numbers of the mean of those numbers is at least:
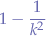
where:

and

Example
Taking values for  (
(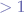 ), we can observe the following:
), we can observe the following:
- for
 , we obtain
, we obtain  , meaning that at least
, meaning that at least  of the values must be within two standard deviations from the mean.
of the values must be within two standard deviations from the mean. - for
 , we obtain
, we obtain  , meaning that at least
, meaning that at least  of the values must be within three standard deviations from the mean.
of the values must be within three standard deviations from the mean. - for
 , we obtain
, we obtain  , meaning that at least
, meaning that at least  of the values must be within four standard deviations from the mean.
of the values must be within four standard deviations from the mean.
Given the previous example, we know that the mean is  and the standard deviation is
and the standard deviation is 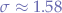 . Now we take values: for
. Now we take values: for  , we have
, we have 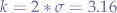 and, subtracting that value from the mean, we obtain the lower bound:
and, subtracting that value from the mean, we obtain the lower bound:  ; then we add the value to the mean, obtaining the upper bound:
; then we add the value to the mean, obtaining the upper bound:  meaning that at least
meaning that at least  of the values must be between the lower bound
of the values must be between the lower bound  and the upper bound
and the upper bound  . The same can be performed for other values of
. The same can be performed for other values of  .
.
For the contact, copyright, license, warranty and privacy terms for the usage of this website please see the contact, license, privacy, copyright.



