Shortnote

The following script will accept a notecard that contains any number of linear equations with any number of unknowns provided via a notecard. Assuming that the number of unknowns is equal to the number of equations, the calculator will then compute the unknowns and display them using overhead text.

The script is able to solve linear systems with any number of equations and unknowns. This is done by using Laplace matrix manipulations using the functions that we have gathered in the matrices section.

Video

Using the Calculator

The package you have received from marketplace contains three testing notecards with equations.

Once the calculator is rezzed, you can drop a notecard inside the calculator and touch to find out the unknowns. To replace the notecard, edit the calculator and delete the old notecard. Then drop a new notecard in the calculator.

Test Scenarios

This example is taken from a previous version that prints out the result in local chat. However, the final version displays the results using overhead text.

Given a notecard with the following two equations:

x + y = 2
y = 3

the calculator will print the values for $x$ and $y$ :

[WaS-K]: Linear Equation Calculator: -------------
[WaS-K]: Linear Equation Calculator: x=-1.000000
[WaS-K]: Linear Equation Calculator: y=3.000000
[WaS-K]: Linear Equation Calculator: -------------

Similarly, for three unknowns and three equations:

x + y = 10
2x + z = 1
z + x = 3

the primitive will print out the values of $x$ , $y$ and $z$ :

[WaS-K]: Linear Equation Calculator: -------------
[WaS-K]: Linear Equation Calculator: y=12.000000
[WaS-K]: Linear Equation Calculator: z=5.000000
[WaS-K]: Linear Equation Calculator: x=-2.000000
[WaS-K]: Linear Equation Calculator: -------------

Notecard Limitations

The notecards have to contain reduced equations, line-by-by line with any number of unknowns and without repetitions. For example, the following line is a valid equation line:

x + y = 1

However, the following line is not supported:

x + x + y = 1

since that can be further reduced to 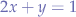$2x + y = 1$ which is suported.

Similarly, the following equation line is not supported:

x + y + 5 = 5

since that can be further reduced to 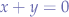$x + y = 0$ which is supported.

Code

///////////////////////////////////////////////////////////////////////////
//    Copyright (C) 2012 Wizardry and Steamworks - License: GNU GPLv3    //
///////////////////////////////////////////////////////////////////////////
list wasSubtractSubList(list input, list delete) {
    do {
        string tok = llList2String(delete, 0);
        list clean = input;
        do {
            if(llList2String(clean, 0) == tok) {
                integer idx = llListFindList(input, (list)tok);
                input = llDeleteSubList(input, idx, idx);
            }
        } while(clean = llDeleteSubList(clean, 0, 0));
    } while(delete = llDeleteSubList(delete, 0, 0));
    return input;
}
 
///////////////////////////////////////////////////////////////////////////
//    Copyright (C) 2012 Wizardry and Steamworks - License: GNU GPLv3    //
///////////////////////////////////////////////////////////////////////////
// transposes a square matrix of ord columns
list wasMatrixTranspose(list matrix, integer ord) {
    list result = [];
    integer mLength = llGetListLength(matrix);
    integer j = 0;
    do {
        integer i = j;
        do {
            result += llList2String(matrix, i);
            i += ord;
        } while(i<mLength);
    } while(++j<ord);
    return result;
}
 
///////////////////////////////////////////////////////////////////////////
//    Copyright (C) 2012 Wizardry and Steamworks - License: GNU GPLv3    //
///////////////////////////////////////////////////////////////////////////
// returns the unsigned cofactor of matrix m with ord 
// columns with the pivot r, respectively c.
list wasMatrixCofactor(list m, integer r, integer c, integer ord) {
    integer idx = 0;
    integer i = 0;
    do {
        integer j = 0;
        do {
            if(i == r || j == c) m = llListReplaceList(m, (list)" ", idx, idx);
            ++idx;
        } while(++j<ord);
    } while(++i<ord);
    return wasSubtractSubList(m, [" "]);
}
 
///////////////////////////////////////////////////////////////////////////
//    Copyright (C) 2012 Wizardry and Steamworks - License: GNU GPLv3    //
///////////////////////////////////////////////////////////////////////////
list wasMatrixAdjugate(list m, integer ord) {
    list result = [];
    integer i = 0;
    do {
        integer j = 0;
        integer o = -1;
        if(i % 2 == 0) jump compute;
        o = 0;
@compute;
        do {
            list cof = wasMatrixCofactor(m, i, j, ord);
            if(o = ~o) {
                result += -wasDeterminant(cof, ord-1);
                jump next;
            }
            result += wasDeterminant(cof, ord-1);      
@next;
        } while(++j<ord);
    } while(++i<ord);
    return wasMatrixTranspose(result, ord);
}
 
///////////////////////////////////////////////////////////////////////////
//    Copyright (C) 2012 Wizardry and Steamworks - License: GNU GPLv3    //
///////////////////////////////////////////////////////////////////////////
// returns the inverse of an matrix m with adjugate
// adjugate and determinant determinant.
list wasMatrixInverse(list adjugate, float determinant) {
    // assert(determinant) != 0
    if(llGetListLength(adjugate) == 0) return [];
    float e = llList2Float(adjugate, 0);
    adjugate = llDeleteSubList(adjugate, 0, 0);
    return e/determinant + wasMatrixInverse(adjugate, determinant);
}
 
///////////////////////////////////////////////////////////////////////////
//    Copyright (C) 2012 Wizardry and Steamworks - License: GNU GPLv3    //
///////////////////////////////////////////////////////////////////////////
// calulates the determinant of a matrix m with ord 
// columns.
float wasDeterminant(list m, integer ord) {
    float result = 0;
    integer i = 0;
    integer o = -1;
    do {
        //i * cof (i) - i * cof(i) + i * cof(i) - ...
        list cof = wasMatrixCofactor(m, 0, i, ord);
        if(llGetListLength(cof) == 2) {
            if(o = ~o) {
                result -= llList2Float(m, i) * llList2Float(cof, 0);
                jump next;
            }
            result += llList2Float(m, i) * llList2Float(cof, 0);
            jump next;
        }
        if(llGetListLength(cof) == 0) return llList2Float(m, i);
        if(o = ~o) {
            result -=  llList2Float(m, i) * wasDeterminant(cof, ord-1);
            jump next;
        }
        result +=  llList2Float(m, i) * wasDeterminant(cof, ord-1);
@next;
    } while(++i<ord);
    return result;
}
 
///////////////////////////////////////////////////////////////////////////
//    Copyright (C) 2012 Wizardry and Steamworks - License: GNU GPLv3    //
///////////////////////////////////////////////////////////////////////////
// returns the dot-product of two matrices providing that
// the number of columns (ord_m) of matrix m is equal to
// the number of rows of matrix n
list wasMatrixDotProduct(list m, list n, integer ord_m, integer ord_n) {
    list result = [];
    integer i = 0;
    integer j = 0;
    do {
        do {
            integer sub_i = i;
            integer sub_j = j;
            float val = 0;
            do {
                val += llList2Float(m, sub_i) * llList2Float(n, sub_j);
                sub_j += ord_n;
                ++sub_i;
            } while(sub_j<llGetListLength(n));
            result += val;
        }
        while(++j<ord_n);
        i+=ord_m;
        j=0;
    } while(i<llGetListLength(m));
    return result;
}
 
key nQuery = NULL_KEY;
integer nLine = 0;
list mParameters = [];
list mResults = [];
list mUnknowns = [];
list mInput = [];
integer eCount = 0;
integer columns = 0;
string nName = "";
 
default {
    state_entry() {
        integer itra = llGetInventoryNumber(INVENTORY_NOTECARD);
        if(itra >0) jump found_notecard;
        llSetText("Please insert notecard.", <0,1,0>, 1);
        return;
@found_notecard;
        llSetText("Reading notecard.\nPlease wait...", <1,1,0>, 1);
        nName = llGetInventoryName(INVENTORY_NOTECARD, 0);
        nQuery = llGetNotecardLine(nName, nLine);
    }
 
    dataserver(key id, string data) {
        if(id != nQuery) return;
        if(data == EOF) {
            integer s = llGetListLength(mInput)-1;
            do {
                string tok = llList2String(mInput, s);
                do {
                    string stok = llGetSubString(tok, 0, 0);
                    if(stok != "+" && stok != "-" && stok != "0" && stok != "\n" && stok != "=" && (float)stok == 0) {
                        if(llListFindList(mUnknowns, (list)stok) == -1)
                            mUnknowns += stok;
                    }
                    tok = llDeleteSubString(tok, 0, 0);
                } while(llStringLength(tok));
            } while(--s>-1);  
            list proc = llParseString2List(llDumpList2String(mInput, ""), ["\n"], []);
            integer p = 0;
            do {
                string line = llList2String(proc, p);
                list sepEq = llParseString2List(line, ["="], []);
                mResults += llList2Float(sepEq, 1);
                list eq = llParseString2List(llList2String(sepEq, 0), [], mUnknowns);
                integer u = llGetListLength(mUnknowns)-1;
                do {
                    string unknown = llList2String(mUnknowns, u);
                    integer idx = llListFindList(eq, (list)unknown);
                    if(idx == -1) {
                        mParameters += 0;
                        jump next_unknown;
                    }
                    if(idx == 0) {
                        mParameters += 1;
                        jump next_unknown;
                    }
                    string nib = llList2String(eq, idx-1);
                    if(nib == "+" || nib == "-") {
                        mParameters += (float)(nib+"1");
                        jump next_unknown;
                    }
                    mParameters += llList2Float(eq, idx-1);
@next_unknown;
                } while(--u>-1);
            } while(++p<llGetListLength(proc));
            llSetText("Touch to compute!", <0,1,0>, 1);
            return;
        }
        if(data == "") jump next_line;
        mInput += llParseString2List(data, [" "], ["+", "-"]) + "\n";
        ++eCount;
@next_line;
        nQuery = llGetNotecardLine(nName, ++nLine);
    }
 
    touch_start(integer num) {
        if(eCount != llGetListLength(mUnknowns)) {
             llSetText("The number of unknowns\nmust match the\nnumber of equations!", <1,0,0>, 1);
             return;
        }
        if(eCount < 2 || llGetListLength(mUnknowns) < 2) {
            llSetText("Nothing to calculate.", <1,0,0>, 1);
            return;
        }
        state compute;
    }
 
    changed(integer change) {
        if(change & CHANGED_INVENTORY) llResetScript();
    }
    on_rez(integer num) {
        llResetScript();
    }
}
 
state compute
{
    state_entry()
    {
        llSetText("Computing...", <1,1,0>, 1);
        list solutions = wasMatrixDotProduct(wasMatrixInverse(wasMatrixAdjugate(mParameters, eCount), wasDeterminant(mParameters, eCount)), mResults, eCount, 1);
        string result = "";
        do {
            result += llList2String(mUnknowns, llGetListLength(mUnknowns)-1) + "=" + (string)llList2Float(solutions, 0) + "\n";
            mUnknowns = llDeleteSubList(mUnknowns, llGetListLength(mUnknowns)-1, llGetListLength(mUnknowns)-1);
            solutions = llDeleteSubList(solutions, 0, 0);
        } while(llGetListLength(solutions));
        llSetText(result, <0,1,1>, 1);
    }
    changed(integer change) {
        if(change & CHANGED_INVENTORY) llResetScript();
    }
    touch_start(integer num) {
        llResetScript();
    }
}

Table of Contents