Mapping an Obstacle Course

Picture Plot	3D Video Plot

Preliminary graph observations:

The graph looks rotated compared to the image in the video, perhaps something to do with the local axes being different and asking for llGetPos. The right part of the cuboid seems to be z (not sure, needs more data). One of those free mouse-drag-and-rotate graphs would be cool, gnuplot gives major headaches.
The very first observation that we can make is that the Great Wanderer finds itself in a cuboid-shaped enclosure. The extreme collision-cloud formations join up, being quite parallel to the axes.
Based on the former, we can preliminarily conclude that the cuboid is resting on flat ground. That is, the ground underneath the enclosure is flat.
From the graph, we can see that the cage (see video) is placed approximately at 24.5 meters above the water level (the z-axis gives that away).
We can observe that the box indeed spans approximately 5m on all three axes:
- For x: $36-31.5 =4.5m$
- For z: $29-24.5=4.5m$ .
- For y: $48-43.5=4.5m$ .

Makes sense, I just jammed the walls in and did not care to much about creating a perfect 5x5x5 cube. By jamming them in, I probably reduced the dimensions by .5m, getting close to the 4.5m from our calculations.

Furthermore, the cloud formation in the bottom right corner on the graph at approx $(36,47.5,24.5)$ , if you look at it closely, almost gives the contour of the corner.
The coordinates, along the $x$ -axis of the graph are growing and the coordinates along the $y$ -axis are growing as well. That means that the box is positioned with the bottom left corner (close to 31.5 value on the bottom left part of the graph) towards the region's origin $(0,0,0)$ .
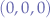Based on the former, we know the box is positioned approximately 31.5mx43.5m away from the region's origin $(0,0,0)$ .
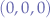Based on the former, the enclosure is facing North with its top forward face (the unmarked scale, not the one one the left).
We have two cloud-formations in the middle, hinting that we have objects on the interior of the enclosure with which the Great Wanderer collided a few times.