I've been toying around with lagoons and trying to simulate the bioluminescence by using the PRIM_GLOW parameter for primitives. I have started from a book called Algal Cultures and Phytoplankton Ecology,G. E. Fogg, and Brenda Thake 1965 which, several pages lower, illustrates some graph plots of how algae absorb light.

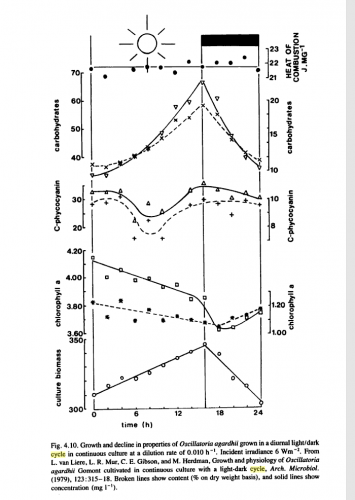
The most interesting plot, is the one that we cite in Figure 1. which shows the heat of the combustion relative to the time in hours. Apparently, the peak is at 1600 hours when the algae radiates light due to the processing of light within the algae cells.

In order to accomplish that in SecondLife, I have first attempted to use the usual if-else clauses in order to achieve the slopes. However that complicated the script a lot and, even by adding magic numbers, the result was neither clean nor correct enough. Lastly, I tried to approximate the curve in above in Figure 1. by using trigonometry. The carbohydrates slope and the culture biomass approximately resemble a sinus slope.

A good tool to use would be llGetWallclock to grab the number of hours in 24 hour format. In that case, we have to map the interval as well as the cutoff-point to the sinus curve. For that, I wrote a script to display the hours and map sine values to radians in order to use the result as a parameter for PRIM_GLOW.

bioluminesence.lsl

//////////////////////////////////////////////////////////
//   (C) Wizardry and Steamworks 2011, license: GPLv3   //
//////////////////////////////////////////////////////////
float wasBioLuminescence(float hours) {
    float sin = llSin(0.1*hours);
    if(sin>0.5) return sin-0.5;
    return sin;
}
 
default
{
    state_entry() {
        llOwnerSay("---MARK---");
        integer hours = 0;
        do {
            llOwnerSay("Hour: " + (string)hours + ". wasBioLum:" + (string)wasBioLuminescence(hours));
        } while(++hours<24);
        llOwnerSay("---MARK---");        
    }
}

Using that, we generate a table that maps hours to radians which will become the value that will be passed to llSetPrimitiveParams:

Object: ---MARK---
Object: Hour: 0. wasBioLum:0.000000
Object: Hour: 1. wasBioLum:0.099833
Object: Hour: 2. wasBioLum:0.198669
Object: Hour: 3. wasBioLum:0.295520
Object: Hour: 4. wasBioLum:0.389418
Object: Hour: 5. wasBioLum:0.479426
Object: Hour: 6. wasBioLum:0.064642
Object: Hour: 7. wasBioLum:0.144218
Object: Hour: 8. wasBioLum:0.217356
Object: Hour: 9. wasBioLum:0.283327
Object: Hour: 10. wasBioLum:0.341471
Object: Hour: 11. wasBioLum:0.391207
Object: Hour: 12. wasBioLum:0.432039
Object: Hour: 13. wasBioLum:0.463558
Object: Hour: 14. wasBioLum:0.485450
Object: Hour: 15. wasBioLum:0.497495
Object: Hour: 16. wasBioLum:0.499574
Object: Hour: 17. wasBioLum:0.491665
Object: Hour: 18. wasBioLum:0.473848
Object: Hour: 19. wasBioLum:0.446300
Object: Hour: 20. wasBioLum:0.409297
Object: Hour: 21. wasBioLum:0.363209
Object: Hour: 22. wasBioLum:0.308496
Object: Hour: 23. wasBioLum:0.245705
Object: ---MARK---

Which gives some pretty neat results, approximately matching the curve from Figure 1. We can match the conclusions to real life since if you stroll on the beach after a sunset, you will see the waves perfectly although there isn't any light source - combustion still taking place. Also, long time after the sun has set, 2300 hours+ you will see a clear reflection of the moon on the pool without seeing the waves flaring up - combustion is close to zero.

bioluminescence_clock.lsl

//////////////////////////////////////////////////////////
//   (C) Wizardry and Steamworks 2011, license: GPLv3   //
//////////////////////////////////////////////////////////
float wasBioLuminescence(float hours) {
    float sin = llSin(0.1*hours);
    if(sin>.5) return sin-.5;
    return sin;
}
 
default
{
    state_entry() {
        llSetPrimitiveParams([PRIM_GLOW, ALL_SIDES, wasBioLuminescence(llGetWallclock()/3600)]);
        llSetTimerEvent(3600);
    }
    timer() {
        llSetPrimitiveParams([PRIM_GLOW, ALL_SIDES, wasBioLuminescence(llGetWallclock()/3600)]);
    }
}