The wasBinarySearchTreeInsert function takes as arguments:

• a binary search tree (BST) as a flattened list as per binary_trees.
• the root of the binary search tree (root)
• the node (node) to insert into the binary search tree.

and returns the resulting binary search tree.

// Ord() function, written by Pedro Oval, 2010-05-28
// Inlined by Wizardry and Steamworks
integer Ord(string chr) {
    if (chr == "") return 0;
    string hex = llEscapeURL(chr);
    if (llGetSubString(hex, 0, 0) != "%") 
        return llBase64ToInteger("AAAA" + 
            llStringToBase64(llGetSubString(chr, 0, 0)));
    integer b = (integer)("0x" + llGetSubString(hex, 1, 2));
    if (b < 194 || b > 244) return b;
    if (b < 224) return ((b & 0x1F) << 6) | 
        (integer)("0x" + llGetSubString(hex, 4, 5)) & 0x3F;
    if (b < 240) return (b & 0x0F) << 12 + 
        ((integer)("0x" + llGetSubString(hex, 4, 5)) & 0x3F) << 6 + 
        (integer)("0x" + llGetSubString(hex, 7, 8)) & 0x3F;
    return (b & 0x07) << 18 + 
        ((integer)("0x" + llGetSubString(hex, 4, 5)) & 0x3F) << 12 + 
        ((integer)("0x" + llGetSubString(hex, 7, 8)) & 0x3F) << 6 + 
        (integer)("0x" + llGetSubString(hex, 10, 11)) & 0x3F;
}
 
///////////////////////////////////////////////////////////////////////////
//    Copyright (C) 2013 Wizardry and Steamworks - License: GNU GPLv3    //
///////////////////////////////////////////////////////////////////////////
integer wasOrdCompare(string chra, string chrb) {
    // numerical
    float fa = (float)chra;
    float fb = (float)chrb;
    if(fa != 0 && fb != 0) {
        if(fa > fb) return 1;
        if(fa < fb) return -1;
        return 0;
    }
    // lexical
    if(llStringLength(chra) == 0 && llStringLength(chrb) == 0) return 0;
    if(llStringLength(chra) && llStringLength(chrb) == 0) return 1;
    if(llStringLength(chra) == 0 && llStringLength(chrb)) return -1;
    string a = llGetSubString(chra, 0, 0);
    chra = llDeleteSubString(chra, 0, 0);
    string b = llGetSubString(chrb, 0, 0);
    chrb = llDeleteSubString(chrb, 0, 0);
    integer oa = Ord(a);
    integer ob = Ord(b);
    if(oa > ob) return 1;
    if(oa < ob) return -1;
    return wasOrdCompare(chra, chrb);
}
 
///////////////////////////////////////////////////////////////////////////
//    Copyright (C) 2013 Wizardry and Steamworks - License: GNU GPLv3    //
///////////////////////////////////////////////////////////////////////////
list wasBinarySearchTreeInsert(list BST, string root, string node) {
    integer i = llListFindList(BST, (list) root);
    string pivotRoot = llList2String(BST, i);
    string left = wasBinaryTreeLeft(BST, pivotRoot);
    string right = wasBinaryTreeRight(BST, pivotRoot);
    integer compare = wasOrdCompare(node, pivotRoot);
    if (compare > 0) {
        if (right == "") {
            if (left == "") while (llGetListLength(BST) < 2 * i + 2) BST += "";
            return llListReplaceList(BST, (list) node, 2 * i + 2, 2 * i + 2);
        }
        return wasBinarySearchTreeInsert(BST, right, node);
    }
    if (compare < 0) {
        if (left == "") {
            if (right == "") while (llGetListLength(BST) < 2 * i + 1) BST += "";
            return llListReplaceList(BST, (list) node, 2 * i + 1, 2 * i + 1);
        }
        return wasBinarySearchTreeInsert(BST, left, node);
    }
    llSay(DEBUG_CHANNEL, "ERROR: Invariant violation; BST must contain unique values.");
    return [];
}

Suppose that initially, we have an empty binary search tree, after which we insert the following letters in sequence: "M", "E", "R", "L", "I", "N". The resulting binary search tree should have the following structure:

       M               
      / \       
     /   \      
    /     \     
   /       \    
   E       R       
    \     /     
     \   /      
     L   N       
    /           
    I           

We can test that with the script above using the following successive calls:

        // start off with the empty list
        list in = [ "" ];
        // insert M
        in = wasBinarySearchTreeInsert(in, "M", "M");
        // insert E
        in = wasBinarySearchTreeInsert(in, "M", "E");
        // insert R
        in = wasBinarySearchTreeInsert(in, "M", "R");
        // insert L
        in = wasBinarySearchTreeInsert(in, "M", "L");
        // insert I
        in = wasBinarySearchTreeInsert(in, "M", "I");
        // insert N
        in = wasBinarySearchTreeInsert(in, "M", "N");
        // print out the flattened tree.
        llOwnerSay(llDumpList2String(in, " | " ));

The result is printed out as:

[16:51]  Binary Search Tree: M | E | R |  | L | N |  |  |  | I

Now, let's take "M E R L N I" and check the left and right children of every node to see whether the result is correct. As per the binary trees notation the left child of a node can be found at and the right child of a node can be found at 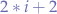where i is the index of the current node.