Table of Contents
About
The following is a description of a cannon, created by Wizardry and Steamworks and offered freely on marketplace, that is designed to calculate and display various firing parameters. It is a simplistic variation on artillery since the cannon does not fire automatically but instead allows the user to control the firing parameters. Possible applications can include role-play simulators or the like and possibly an implementation of the various tank-like games (Worms, etc...).
Video
Exports
Assets
| Asset | Description |
|---|---|
| Cannon Firing Sound |
Using
- Unpack the jute and extract the cannon, sample wall and quick help document.
- Rez the cannon.
- Place the wall somewhere no further than
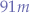 away from the cannon.
away from the cannon. - Use the arrows on the cannon gear box to rotate the cannon and elevate the barrel.
- Long-press (left-click and hold) the barrel to accumulate velocity.
- Release the left mouse button and the cannon will fire.
Sample Wall and Possible Applications
The sample wall contains the health script and can be molded into a different object. Or, the script can be taken out and placed in an entirely different build. When the health meter reaches zero, the script pauses for one second and then derezzes the build.
It is possible to build a small enclosure around the cannon and play a tank-like game where each player must destroy the other players' fortresses.
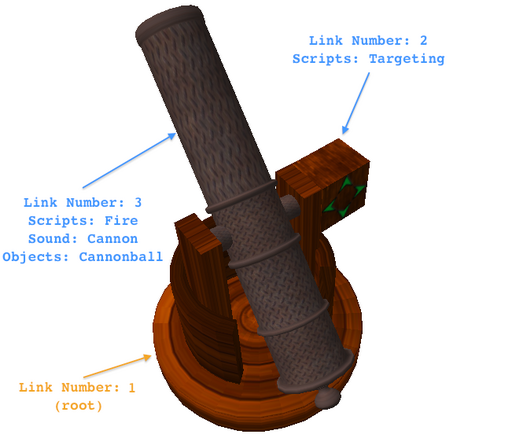
The Build
Physics
The following section describe the various calculations performed by the cannon. These calculations not only determine the firing velocity but computes various data for the overhead text. The cannon computes the horizontal distance (grid-distance) to the impact coordinates and also displays the nozzle elevation.
Calculating Time to Maximal Altitude
The initial velocity increments linearly by touch-and-holding the cannon barrel. When the avatar stops touching the barrel, the cannonball is fired with the accumulated velocity.
The velocity vectors for  and
and  where
where  represents the horizontal axis and
represents the horizontal axis and  represents the elevation are given by:
represents the elevation are given by:
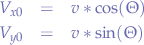
When the vertical component is zero at peak altitude, we have that:
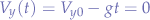
thus, extracting  , the time to reach the peak altitude, we obtain:
, the time to reach the peak altitude, we obtain:
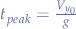
Substituting Values
By design we have that the capped maximum velocity ( ) of the cannon is
) of the cannon is 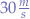 . We also know that the maximal distance can be obtained by making
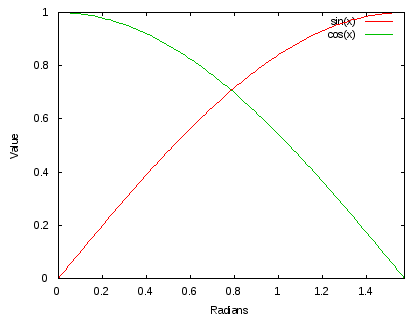
. We also know that the maximal distance can be obtained by making  . This is because of the
. This is because of the  and
and  functions overlap at
functions overlap at  :
:
Would we have chosen any angle so that 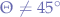 , then the
, then the  and
and 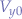 would have started to decrease, one in function of the other.
would have started to decrease, one in function of the other.
Thus, substituting for  and
and 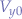 , we have:
, we have:
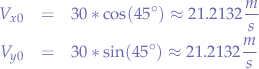
And  at peak altitude, since the gravitational acceleration is
at peak altitude, since the gravitational acceleration is  :
:
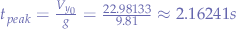
Finding Horizontal Distance Travelled
Deriving  in time, we have that:
in time, we have that:
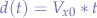
Since it takes the same amount of time to reach maximum altitude as it takes to fall back down, we have that:
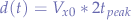
Substituting Values
We obtain that for a maximum elevation of  and a maximum firing velocity of
and a maximum firing velocity of 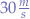 , the horizontal travel distance is:
, the horizontal travel distance is:
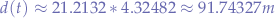
which gives us the maximum firing range for the cannon.
Limitations
- The maximum firing distance is given from the above calculations as
 .
. - The maximum firing velocity is
 .
. - The minimum firing velocity is capped at
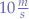 . This is to ensure that the projectile travels through the barrel (since the projectile rezzes at the centre of the barrel and is not bounded by the barrel's dimensions).
. This is to ensure that the projectile travels through the barrel (since the projectile rezzes at the centre of the barrel and is not bounded by the barrel's dimensions). - The maximum elevation of the barrel is
 starting from
starting from 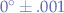 .
.
Index
For the contact, copyright, license, warranty and privacy terms for the usage of this website please see the contact, license, privacy, copyright.