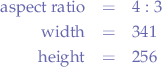Table of Contents
Converting Between Aspect Ratios (Distorting)
Since most programs do not provide a straight-forward way of doing this, here is a quick way of converting between aspect ratios. The aspect ratio represents the ratio between the width of the image and the height of the image such that an aspect ratio of 2:1 just means that the picture is two-times wider than tall.
Since it is just a ratio, we can write that:
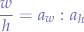
the semi-colon was used in old-school maths terminology for fraction which means that 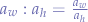 such that:
such that:
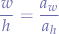
Now, suppose that we want to distort the same width and height to a different ratio, say 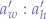 such that:
such that:
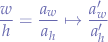
This means that we must multiply the left-hand side fraction with a constant that will transform the ratio 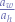 to
to  . Let that constant be called
. Let that constant be called  , such that:
, such that:
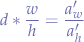
Now, we extract  from the equation, and we obtain:
from the equation, and we obtain:
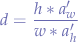
which will give us a numeric constant that should be multiplied with whatever is larger: either the width of the picture  or the height of the picture
or the height of the picture  . If that is the case then we can derive the following transformation function:
. If that is the case then we can derive the following transformation function:
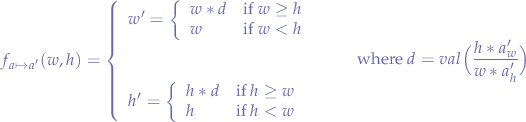
that, when applied to:
- a known width
 ,
, - a known height
 ,
, - the numeric value of
 computed using the
computed using the- destination aspect ratio
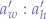
will return a new width 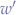 and a new height
and a new height 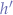 , effectively distorting an aspect ratio
, effectively distorting an aspect ratio  to a destination aspect ratio
to a destination aspect ratio 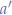 .
.
Example
The back-office story about this, is that the image on the right is the original image and was uploaded to some software that distorted it (damaged it, if you will) to a 2:1 ratio and we were trying to get the original back as it was.
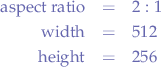
Thus, we want to convert the image on the left, which is a 2:1 aspect-ratio image to a 4:3 aspect ratio image on the right. Let us enumerate what we know that:
- the image on the left is
512pixels wide and, 256pixels tall and that we want,- an aspect ratio of
4:3.
In other words, we have that:
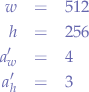
which we can then plug-in to compute the numeric value of  :
:
![Equations \begin{eqnarray*}
d&=&\frac{256*4}{512*3} \\
&=&\frac{2}{3} \\
&\approx& 0.666[6]
\end{eqnarray*}](/lib/exe/fetch.php?media=wiki:latex:/img22df2fdfac518396bc69e887bcb16e97.png)
Since we have now obtained  , we can use our transformation function
, we can use our transformation function 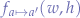 in order to calculate the new width and height of the resulting image on the right.
in order to calculate the new width and height of the resulting image on the right.
![Equation $$
f_{a \mapsto a'}(w,h) =
\left\{
\begin{array}{ll}
512 *0.666[6] \approx 341.333[3]
\right. \\
256
\end{array}
\right.
$$](/lib/exe/fetch.php?media=wiki:latex:/img7bcd89620ed734395466189aab98067c.png)
So the new image should have a width of 341 pixels (rounded-up) and a height of 256 pixels.
Quality
Using this method, the quality of the image is, in-fact enhanced: a stretching of an image will reduce the quality of an image, whereas a distort to its original size will increase the quality of the image. This is due to how pixels merge in various algorithms?
When changing the image size, the various filters such as nearest neighbor, bicubic, bilinear etc... Perform some sort of interpolation where the color of the pixels of the newly generated image are determined by examining neighboring pixels.
The problem is that when you enlarge an image, the colors fade, imagine this like stretching a very soft paper bag until it rips, and the new image, when observed at actual size appears blurry.
When you compress or downsize and image, the algorithms will tend to actually refine the value of every individual pixel. For example, if you scale a very large image (and hence, containing lots of "data") to a smaller image, the algorithms will tend to offer a more detailed view of the resulting image - simply because the averaging process had a lot of data to compute the new pixels.
Adobe says it's the other way round - they've never scaled a wallpaper, they don't know what they're coding. 
Resizing without Loss
One common issue you have is that you obtain an image of a given width and height and would like to fit it on a screen of a different width and length. Most graphics programs call have an option called "preserve aspect ratio" that, when activated, will calculate either the resulting width and height when the image is resized.
Keeping in mind the previous section, we define that:
- enlarging an image will reduce the quality of the image,
- shrinking an image will not reduce the quality of the image.
The goal is to resize the image:
- whilst keeping the largest possible area, and
- not reducing the quality of the image,
- preserving the orientation of the image.
Suppose there is an image of a given original width and height (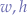 ) and that the screen that the image has to be resized to is of a different width and height (
) and that the screen that the image has to be resized to is of a different width and height (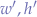 ). Computing the ratio of the first image
). Computing the ratio of the first image  and the ratio of the destination image
and the ratio of the destination image  , the ratio of the first image
, the ratio of the first image  and the ratio of the second image
and the ratio of the second image  is obtained.
is obtained.
- When
 , the image will fit by shrinking the original image when
, the image will fit by shrinking the original image when  or, without shrinking the original image when
or, without shrinking the original image when 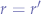 .
.
This means, at least, that the original image will have to be larger or equal to the destination image.
- When both ratios
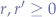 or
or  then the area necessary to be cropped in order to convert the original image into the destination image is far more than the area necessary to be cropped when
then the area necessary to be cropped in order to convert the original image into the destination image is far more than the area necessary to be cropped when  and
and  or
or  and
and  .
.
For the contact, copyright, license, warranty and privacy terms for the usage of this website please see the contact, license, privacy, copyright.