Table of Contents
An Universal Symphony
- We name a sound blurr, the action of dissolving the high pitched sounds so that they fade-in with other sounds.
This contrasts well to a blurr in graphics terms which dissolves pixels and bringing their RGB values closer together. We apply that concept to sounds.
Combinators
- We map a Monophthong to an
 sound combinator consisting of one dominant high-pitched sound (1).
sound combinator consisting of one dominant high-pitched sound (1).-
- We call a "Quadthongs" composition, a sound combinator consisting of two composed
 dominant high-pitched sounds.
dominant high-pitched sounds.
- We call a Triphthong composition, sound combinator consisting of three
 dominant high-pitched sounds.
dominant high-pitched sounds.
-
- We map a Hiatus to a
 a pause or a dampening of a previous combinator which separates combinators.
a pause or a dampening of a previous combinator which separates combinators.
Compositions
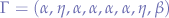
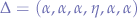
Which, we believe, are all natural occurring sound-patterns. The number of  primary combinators between
primary combinators between  -combinators may be composed of alternating pitches, yet still "dominant" enough to preserve the pattern of the compositions.
-combinators may be composed of alternating pitches, yet still "dominant" enough to preserve the pattern of the compositions.
There may be others. . .
Observations

The primary combinators which are part of the  composition may be produced by any event occurring in nature, although possibly blurred as per the first chapter. The sequence of the composition holds through the
composition may be produced by any event occurring in nature, although possibly blurred as per the first chapter. The sequence of the composition holds through the dominant nature of  , respectively
, respectively  combinators, as well as the relatively-short time span between them.
combinators, as well as the relatively-short time span between them.
Of course they are naturally occuring sound patterns, they are the most basic sounds (and compositions) one can create! If that is so, then any sound-pattern can be derived from these combinators by playing on hiatuses and pitch: increase and lower the pitch and get a distinction between  -combinators and hiatuses.
-combinators and hiatuses.
As for the origins of the combinators ( and
and  ), that is still a mystery to be solved. A good example is any movie you have seen recently: honks, machines, gunfire, coughs, barks. The used combinators are all
), that is still a mystery to be solved. A good example is any movie you have seen recently: honks, machines, gunfire, coughs, barks. The used combinators are all  ,
,  and sometimes even
and sometimes even  or
or  combinators (very, very many examples, look for them).
combinators (very, very many examples, look for them).
Examples
The primary combinators, the compositions can be created by:
- objects (mouse clicks, gunfire)
- animals
- coughs
- fire crackling, embers.
It may be that the combinators can be found in music, but as a consequence since music is not made of randomly occurring sounds. It is possible that each "pulse" may follow from different sources, ie: several objects together that create  or
or  combinators.
combinators.
Pattern
| 1 | 2 |
|---|---|
Postal
Example of several  combinators start at 4:40, follow the gun shootings.
combinators start at 4:40, follow the gun shootings.
Examples sequences:
- 4:55 to 5:00.
- blurred, from 5:00 to 5:08.
Dog Barks
Right at the start, a  combinator.
combinator.
Fireplace
Two  combinators:
combinators:
- 00:26 to 00:38 followed by many more
Water Flowing into a Sink
Water dripping (sink or shower)
Possible Extensions
It is possible that the patterns are not restricted to sound and that they may be found to occur randomly by light intensity. In that sense, the high pitched "dominant" sounds can be replaced by emphasized pulses and the hiatuses by pauses or decrease in light intensity.
Origin
A speculation could hint to the fact that the human brain is only able to instinctively recognize four "marks" (either sounds or visuals). For example, your brain immediately sees four lines in this sequence:
| | | |
but has to subconsciously count:
| | | | |
five marks.
All distinguishable Combinators are omnipresent, for example:
- the number one is one tap, one point, and right about the simplest sound to make, etc...
- the number two (in any sequence) is easily composed of two "one taps".
- the number three (in any sequence) is found in abundance in nature (three axes, three points define a plane, etc..).
In any case, regardless of origin, the patterns are to be found in the mainstream and the Combinators as well as the Compositions are a consequence (a chaining) of the fact that humans are able to instinctively observe up to four marks.
Imprinting Thesis
Architectural Invariants
A voire Deleuze, Societes de Control
Over the years humans have arrived to a point where they tend, for example, to build houses that have a parallelepiped-like structure. Perhaps humans have decided at some point that building cylindrical buildings with apartments having round-shaped wall would be inefficient, whether in practice or perhaps as a consequence of humans and the way they perceive space or are built themselves. It would seem, given human conditions, to live in a sphere - everything would just end up tumbling to the bottom of the sphere under, say, "gravity" as an architectural invariant.
Whatever the reasons of the choice of geometry for livable spaces, it seems that universally humans have decided to shape their houses overall as parallelepipeds. One consequence of that fact, is that everything in the environment has to interact with a bunch of structures (buildings) that are shaped as parallelepipeds. Whether that is wind, sound, ... perhaps the people living inside parallelepiped-shaped buildings, all properties of the structures are inherited implicitly by everything that interacts with them.
Now given a structure such as a parallelepiped, it is common sense, as an example, that buying furniture that has right-angles will minimize loss of space in such a structure. Were humans to buy, say, round-shaped furniture, a lot of space would be wasted as the round shapes will be tangent to the surface of the walls. Although unverified (?), one could therefrom draw a wild conclusion that overall, given terse marketing data, people overall would prefer to buy, say, rectangle-shaped furniture than furniture with a round-shaped geometry. Would pipes or plumbing in a house tend to be built as a straight line or would it be more likely that pipes would have a round shape?
Although human brains love to generalize since reasoning with a bunch of edge-cases is difficult, it may so happen that certain locations in space are governed by a set of circumstances that may not appear in other locations such that interactions in both environments may lead to majorly different results. It may be, for instance, be possible to find, say, as an example, a bridge under which one would find a very strong gush of wind compared to, say, a different bridge due to different architectural circumstances. Humans would assume small or no variations between both environments although, given unforeseen circumstances, the variations may turn out to be very large.
Nevertheless, there are many very general architectural invariants, especially those created by human beings, that invariably lead to pre-defined and a fixed set of conditions that will then apply to all entities that interact with the architecture.
One could therefore ask questions and answer them by giving simple answers:
- Why is there a common game exploit for all games that gamers manage to pass through walls in games? To which one could answer: in order to reduce the load, many objects, including land geometries in games are set with physics disabled (phantom) and given sufficient time or just serendipity gamers just manage to find those objects. In this case, the fact that game developers set some objects or land geometries to phantom is an architectural invariant. It may appear trivial yet it is remarkable that no-clip exploits apply for all games which is not apparently intuitive.
- Why are cities quieter during the night? Because people (overall) tend to sleep during night-time. In this very trivial case, the architectural invariant would be that people sleep at night - it seems trivial yet the consequences are rather large on the scale of an entire city! Were the trivial invariant (that people sleep at night) to be framed in the context of a deductive problem then the answer could contribute to the answer heuristically: you are in a city, yet it is quieter than usual, why? Perhaps because it is night time?
- Are all architectures of coins identical? Could it happen that some coins, due to their geometry (and, thereby their usage) become eroded unevenly such that the results of a coin-toss may overall not produce an evenly distributed result? No, not all coins are created equal, in fact, as an example for the first question, it appears that a two pound coin has an overall larger probability, compared to other coins, of landing on its side rather than either of its faces.
- An object when dropped under the contraints of gravity, on, say, a table, would have a progressively attenuated fall where the amplitude would decrease over time as the object bounces around eventually to settles. Of course, it remains very difficult to determine exactly what final position the object would have after the attenuated fall however, what one would know is that any object would have an attenuated fall. It would not be useful, albeit partially incorrect, to claim that "the behavior of an object falling on a table" is not repeatable because, at least partly, it is known (under physical invariants such as gravitational acceleration, material type, length of fall and mass of the object) that an object will always be attenuated as it settles under the laws of elasticity. Whilst the former statement would be unuseful, the latter statement could possibly lead to something constructive.
It may so happen, and it usually is, that apparent holistic situations could be, counter-intuitively, severely constrained by different invariants such that the results would not be entirely unpredictible but rather that a decent guess could be formed within probabilistic limits. Conversely, this does not mean that randomness does not exist, but rather that in particular situations randomness may happen to be constrained by invariants that may have an effect on the outcome that could make the result appear to not be random.
Stating that nothing can be known about the behavior of a system due to overwhelming complexity, does not necessarily imply there is no set of invariants, with their consequences, perhaps leading to a rare but more probable and thereby repeatable behaviour of the system, that are just not known yet such that nothing could ever possibly be said - nor would that statement lead to anything useful, in a mathematical sense, were one to attempt and find the cause.
Perhaps certain black swan or singularity events, when apparent unexpected results are observed, could be explained by some constraints with a locality that would remain to be determined. As invariants go, a discussion may be made on the usefulness of a particular invariant, which seems to be the main problem loosely - sometimes even conversely, in case the invariant is free under the variables of the system, in which case the invariant would not be that useful. Quantitatively, perhaps, a different question would arise whether everything about a behaviour just has to be known or whether small variations are permitted for an useful and partly repeatable result.
Would a toy just have to be sentient in order to be a pet in order to attract human sympathy or is it sufficient for a toy to mimick a sufficiently large set of behaviours (known to be behaviours that attract human empathy, as invariants) in order to be a cherished pet?
Examples
Does randomness generate patterns or is randomness never really random IRL (ie: non-discrete universe) but just constrained by (sometimes hard-to-know) invariants created by the architecture?
Tony Hawks Pro Skater 2
As an example, and perhaps related to ubiquitous game cheats, in a computer game called Tony Hawks Pro Skater 2, just by letting the game character move randomly within a level, after a given amount of time, the game character will find an equilibrium point within the level marked in pink on the following map of the level. Either the skater ends up moving along the first or the second pink line but will not change its movement pattern when either of the two cases occur.
The point of equilibrium seems to be reached regardless of the starting position of the game character and does not seem to be related to the traits of the playable characters either. The character will end up moving back and forth between the pink lines and seems to never move from those paths once the equilibrium is reached.
It seems clear that the whole model could be abstracted to random Brownian movement where certain constraints are placed upon the randomness - not the movement, but rather the disposition of the objects within the level.
This example may be a case where the invariant is hard-to-know, in the sense that more than likely the developers of the game just placed objects, even following a pattern related to the gameplay but had no way of knowing that if a skater would not be controlled by a human agent, after a certain time the skater would end up in those two points of equilibrium. It seems very difficult to be able to tell for a fact when designing a game level that the player would end up in those two points of equilibrium.
Of course, one of the challenges remains to determine how much of the invariant can be reduced - is it just the disposition of the objects on the level? Micro-memory leaks (THPS2 after a long runtime ends messed up badly due to that)? What else?
Perhaps a less spooky occurrence of a similar event that would not involve randomness (or less randomness) would be the sequence as illustrated in the following video.
In game terms, this effect is achieved by holding down the rail-slide button and the "focus" button to gain speed while directing the game character towards the margin of the wedge. The effect is achieved by just making the player slide onto the margin of the wedge, at which point the character slides on the edge, as if it were a rail, and changes its direction accordingly towards the direction of motion. Upon meeting the other side, the game considers that the character has met another rail and slides back down to the other side. Compared to the other case, it seems that this instance has a lot less variables and might be more easily traced to the simplification of the physics engine (constant speed, no friction or speed reduction on rails) - however it might be the case that the game considers the peak of the U-shaped wedge to be a single point in space, or some other geometric abnormality, that just may happen to be defined as a rail (by contrast, say, to the hangar plane that happens to have sharp edges but they are not considered to be rails).
Pong
The exact same type of equilibrium can be reached in other games, for instance, in the eldest most successful commercial video game named "Pong", on Atari, as illustrated by deptymaddog5:
The "cheat" consists in moving the bar to a particular geometric point on the board such that the computer AI will always lose against the player.
Fun Saying
"Even a broken clock tells the right time twice per day." - the architectural invariant in this case includes a human assumption of time, the fact that a point on a circle will be met an infinite amount of times as another point on the circle rotates, etc.
Pendulum
Given a pendulum swinging back and forth and given an initial impulse, under the constraints of [gravity, friction, etc.] there is no other place for the ball at the tip of the pendulum to end up at except exactly at the midpoint. The initial impulse gets decreased over time harmonically as the pendulum is slowed down by friction and under the force exerted by the gravity.
The "architectural invariants" in this case include the physical constraints (gravity, friction, etc).
Perhaps also the harmonic attenuation during freefall of a physical object.
Fast Repeating Radio Bursts (FRRBs)
The Political Landscape
Ian Morris arguments in this book "Why the West Rules -- for Now" that the current political landscape has been conditioned over time by various archeological constraints such as [proximity to water, geographic landscape, proximity to food sources, etc.] in order to result in the current situation. Ian Morris even goes as far as to coin the term "lucky latitudes", regions of the earth that have generally and overall been favored by either the fauna or flora, ie: contrasting harsh climates of Siberia with warm regions of Northern Africa.
Essentially this argument justifies that the formation of powers is not entirely arbitrary and as a consequence of random stochastic events but rather could be at least traced to some components that hinge on the disposition of the environment.
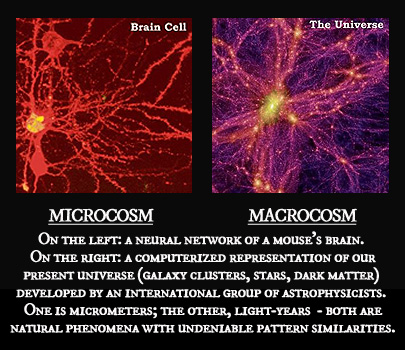
Micro vs. Macrocosmos
The Global Consciousness Project
"It's always still before the storm."
The Global Consciousness Project (GCP) is a thesis that suggests that random number generators would be influenced by thought patterns. Although, we dot legitimize or de-legitimize their efforts, it is worth drawing a parallel that the ideas proposed on this page are somewhat "simpler" compared to the GCP.
For instance, instead of monitoring random number generators, one could choose to monitor, say, major traffic intersections in major cities instead by making the reverse-thesis that at the cusp of major events, there would be distinct human patterns to be observed. Intuitively, this would be derived from trivial observations that people would change their day-to-day behaviours and routines as a reaction to major local or world-wide events. Of course, the GCP would aim towards the goal of predictability and forenotice but our thesis makes a smaller leap of faith, perhaps grounded in nurture rather than nature, that would remain to be determined. In other words, it is clear that world-wide events such as, let's say, a world-wide pandemic would definitely change human patterns (and even traffic flow through intersections), yet it remains to be seen whether that can be predicted by extrapolating from past observations.
Passing the Buck
- https://github.com/avaneev/prvhash - Aleksey Vaneev
- maths is self-referential, but by definition,
- God exists because you believe in God,
- "The span of existence of mathematical rules cannot be estimated, so it is safe to assume they existed for an eternity." is trivially false,
- a perfect circle, or a perfect sphere, is a mathematical construct that exists only in mathematics,
- observer, observable issues perhaps, maths is an useful construct for us, perhaps. . . just for us?
- we are the product of our own selves?
- Grigori Perelman - maybe the concept of "architectural invariants" illustrated where a change in the architecture leads to a definite result other than the former, or, as Perelman, removing holes from a material allows that material to be folded into a sphere.
For the contact, copyright, license, warranty and privacy terms for the usage of this website please see the contact, license, privacy, copyright.