Table of Contents
If you are looking for an autonomous robot system that can roam freely in an enclosed space, you may want to try the extension to Wanderer called Great Wanderer. If you are looking for revolution trajectories, please try orbiter.
ChangeLog
13 August 2012
- Added notes on calibration for sculptures.
15 February 2012
- Added orbiting extension orbiter.
29 January 2012
- Added note about great wanderer, an extension to wanderer.
19 January 2012
- Since I'm working on the PGS, I might as well correct this one as I go.
15 January 2012
- Removed some extra, un-needed computations.
Introduction

I have noticed that there is frequently a need for a script that will move a primitive around randomly. Initially, I have seen this for animal breeders but later I have also seen robots and similar builds. The inspiration came from birds because I have not seen many bird scripts that move the birds by making them fly higher or lower. They all seem to move in a plane without changing altitude. For that, and other applications, I have made the script below to cover most geometrical areas in which a primitive can move. So far I have included:
- movement in a square.
- movement in a circle.
- movement in a sphere.
- movement in a sphere's upper hemisphere relative to the horizon.
- movement in a sphere's lower hemisphere relative to the horizon.
- movement in an elipsoid.
- movement in an upper hemielipsoid relative to the horizon.
- movement in a lower hemielipsoid relative to the horizon.
Also, I wanted to avoid using up the timer event in the script so it can be used by developers to write their own code using the timer event.
For a concise explanation of how wanderer is designed, please see population genetics and selection where we put it to some good use.
Requirements
The primitive this script resides in sets itself to physical. However, it is suggested that phantom should also be turned on to avoid collisions.
Applications
There are several applications I can think of based on the introduction:
- can be used for breeders to move animals around.
- can be used by robots to move around randomly.
- can be used to create birds that move around.
Setup
In case you want to move a sculpted object, it is sometimes necessary to place the object inside an invisible sphere such that llLookAt rotates the object towards the point it is currently wandering to. Otherwise, the object may not face the destination point. Wanderer also accepts some parameters which you can modify in the CONFIGURATION part of the code.
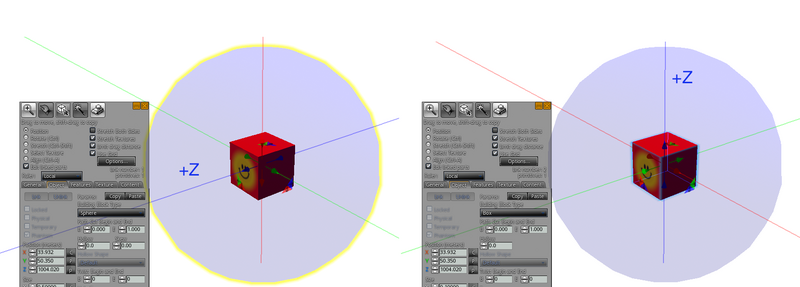
Calibrating Forward Axis For Sculpts
The local  axis of the invisible sphere must be calibrated so that it is aligned with the perceptual "front" of the object. This is because
axis of the invisible sphere must be calibrated so that it is aligned with the perceptual "front" of the object. This is because llLookAt, by definition, rotates the object to point its forward ( ) axis towards a given point. This sometimes conflicts with sculpts because it is not always the case that the
) axis towards a given point. This sometimes conflicts with sculpts because it is not always the case that the  of the root prim is aligned with the perceptual "front" of the object.
of the root prim is aligned with the perceptual "front" of the object.
The local  axis of the object contained in the sphere must point upward. This is because
axis of the object contained in the sphere must point upward. This is because llLookAt rotates the object so that the  axis points downward (or as the specification vaguely puts it, "below the horizon").
axis points downward (or as the specification vaguely puts it, "below the horizon").
Uniformity
The trigonometric functions are decent enough to generate the needed points, however they come at the price of having a cluster of points build up near the centre of the circle or sphere.
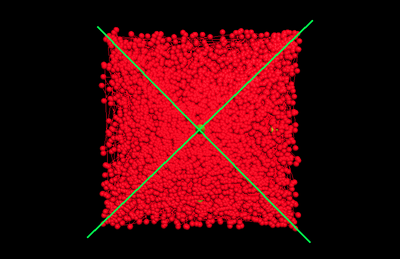
The overly cited Wolfram method is to change the equations so that the square root of the radius is taken instead:
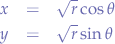
However, that is neither proven or explained. In fact, if we do it the Wolfram way, and plot the points, we get an accumulation of points around the bisectrices of the axes:
If you have a keen eye, you can observe that the points are clustered around the green lines. This does not happen with the sampling method.
In order to do it the sampling way: first, the circle is circumscribed within a square and then points are generated within that square. Then, we check to see whether each of the generated points within that square are within the circle and we eliminate those that are not.
This method is called sampling by rejecting the points that fall outside the bounds of the circle or sphere. The drawback using this method is a slight computational impact: if the randomly selected point falls outside the geometric shape, then a new point has to be generated, hopefully this time within the area of that shape.
The way we do this is using a recursive function that first generates the point, then tests if the point is within the bounds of the geometric shape and if it is, it is returned. If it falls outside the geometric shape, then we call the function again to generate a new point.
Index
The examples use a circle point generator but you can find more generators on the fuss point-generation page.