Table of Contents
Generalization
The great wanderer uses all three axes for movement and makes a distinction based on the directions along those axes: up, down, left, right, forward and backward. These all represent directions along the 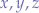 axes in a Cartesian system but does not allow for "fluent" movement where the great wanderer would be aware of any other rotations along the horizon, other than
axes in a Cartesian system but does not allow for "fluent" movement where the great wanderer would be aware of any other rotations along the horizon, other than  rads.
rads.
Let's take for instance a 2-dimensional Cartesian system with two axes  and
and  :
:
,.--'''''--..
,-' y ^ /`-.
,' | / `.
,' | / `.
,' up | / r+ `.
/ |-+ |
| O| | |
| - - - - - +----------> |
| left / | right x |
`. / .'
| / | /
\ / r- down /
`. / | ,'
`._ _,'
`-.__ __.-'
`''''
Up to this point in the article, we notice that the automaton is able to distinguish between "up", "down", "left", "right", "forward" and "backward", which all represent 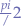 radians rotations around the axes
radians rotations around the axes  ,
, and
and  from origin point
from origin point  . If we simply the model, as shown in the figure above, then we only have 4 directions along the
. If we simply the model, as shown in the figure above, then we only have 4 directions along the  axes.
axes.
We can now circumscribe the Cartesian system inside a circle with  radians and notice that the rays
radians and notice that the rays  and
and  describe two directions along an arbitrary rotation around the
describe two directions along an arbitrary rotation around the  and
and  axes.
axes.
Thus, for all chosen rotations in  radians of the circle we obtain 2 distinct directions:
radians of the circle we obtain 2 distinct directions:  and
and  since the rays are symmetrical. Since we have already said that the great wanderer uses an automaton with 6 states, we can generalize over the states of the automaton in order to expand it so that more directions are possible. We could reverse the situation and simplify the automaton so that it would consist of two states representing directions along "just" the
since the rays are symmetrical. Since we have already said that the great wanderer uses an automaton with 6 states, we can generalize over the states of the automaton in order to expand it so that more directions are possible. We could reverse the situation and simplify the automaton so that it would consist of two states representing directions along "just" the  and
and 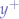 axes. In that case, we would have an automaton with two states, each corresponding to the radian-rotations around the origin point:
axes. In that case, we would have an automaton with two states, each corresponding to the radian-rotations around the origin point:
![Equation $$
QT = [ d(\frac{pi}{2}), d(0) ]
$$](/lib/exe/fetch.php?media=wiki:latex:/imgf3b72259fa2a61c50aed079e39387b7b.png)
Adding back the  and
and  directions, we get an automaton with four states:
directions, we get an automaton with four states:
![Equation $$
QT = [ d(\frac{3*pi}{2}), d(\pi), d(\frac{pi}{2}), d(0) ]
$$](/lib/exe/fetch.php?media=wiki:latex:/img4040adb1e6165f9a86167341f33ded87.png)
Going even further back and by adding the  axes, we obtain another two states, forward and backward:
axes, we obtain another two states, forward and backward:
![Equation $$
QT = [ fwd, bwd, d(\frac{3*\pi}{2}), d(\pi), d(\frac{pi}{2}), d(0) ]
$$](/lib/exe/fetch.php?media=wiki:latex:/img213daab9e208f70f711f2e49c96c77cd.png)
We can observe that the number of angles chosen along the arc of the circle is directly linked to the number of states in the automaton.
We can thus define something called course affinity which would be the number of states that the automaton of a great wanderer would have and it will describe the number of possible directions that the wanderer could both sense (!) and move along.
Geometries
It is also clear that the geometric shape of the great wanderer is related to its course affinity. For example, for a 6-state free roamer, a number of 6 sensors is needed (each symmetrically placed at  -radians) from the centre of the object in order to detect collisions.
-radians) from the centre of the object in order to detect collisions.
Thus, a 6-state automaton would need 6 sensors which describe the 6 directions of the automaton. It is interesting to note that the number of states will always be even for a complete wanderer that senses a direction and its opposite.
up ^ y+
| / forward
+-|---+/ z+
/ | //
/ | //|
left +----|+/ + right
- - - -|- - +|-------->
-x | /|| / x+
| ||/
+-/--|+
| down
backward / y-
z-
Thus, we know that a 6-state automaton will require a symmetrical geometric body with 6 symmetrically placed sensors.
Suppose we additionally add the bisectrices of each plane defined by the 2-combinations of the axes 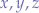 minus the singularities
minus the singularities  ,
,  and
and  . When we add the bisectrices, we are really just rotating the Cartesian system around the origin point by
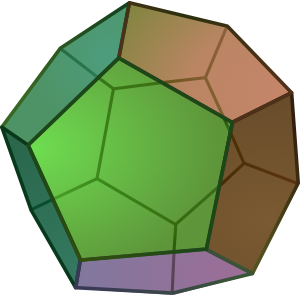
. When we add the bisectrices, we are really just rotating the Cartesian system around the origin point by 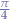 and thereby adding another 6 directions and obtaining thus 12 directions which describe a dodecahedron:
and thereby adding another 6 directions and obtaining thus 12 directions which describe a dodecahedron:
As, we said, we can generalize and observe that the number of faces is given by the rotation of the Cartesian system in 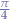 increments, duplicating each time the number of axes and the number of directions.
increments, duplicating each time the number of axes and the number of directions.
For 3 axes, we have 6 directions, and hence 6 faces (cube).
For 6 axes, we have 12 directions, and hence 12 faces (dodecahedron).
For 12 axes, we have 24 directions, and hence 24 faces (24-cube).
For  axes, we have
axes, we have  directions (2n-cube).
directions (2n-cube).
Every time the number of faces being an even number (multiples of 2).
Thus an n-axes wanderer, requires 2n-state automatons with 2n faces. The general formula that maps axes to states is given by:
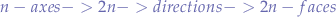
such that each axis requires 2 states, which allows the movement of a generalized great wanderer in  directions.
directions.
Geometric Convergence
We can observe that each time we rotate the Carthesian system in order to generate 2n directions, we are really just generating multiples of 2n-Hypercubes. It is interesting to note that if the even number if faces ( ) were replaced by an uneven
) were replaced by an uneven 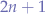 iterator over geometries, we would obtain only theoretical and non-practical geometries which could not be engineered.
iterator over geometries, we would obtain only theoretical and non-practical geometries which could not be engineered.
Also, it is consequential that by increasing the number of faces of a cube, the shape will eventually converge to a sphere - similar to increasing the number of sides of a square which converges to a circle.
Automaton Expansion
Now that we have deduced the correspondence between axes, directions, faces and states, we can automatically generate code that will take as input the number of directions and create an n-great wanderer that moves along those directions.
This is primarily due to the symmetry of the code that great wanderer uses, in which every state is defined by the code-block:
state direction { state_entry() { currentState = "direction"; thrust(currentState); llSetTimerEvent(2); // Anti-stuck. } collision_start(integer num) { state compute; } timer() { llSetTimerEvent(0); if(llFabs(llVecMag(llList2Vector(llGetObjectDetails(llGetKey(), [OBJECT_VELOCITY]), 0))) < ENGINE_SPEED/2) state compute; llSetTimerEvent(1); } }
Thus, by snapping together blocks of code, we can just alter the structure and add states.
The algorithm that is used in order to expand a great wanderer into an n-great wanderer is the following:
- expand the probability array and the named equivalent to n-axes or (2n-axes)-directions:
list qD = [ "forward", "backward", "left", "right", "up", "down", ..., (2n-axes)-drections ]; list QT = [ .15, .17, .17, .17, .17, .17, ..., (2n-axes)-directions, probabilities ];
where the  is a bijective map where each element of
is a bijective map where each element of 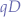 maps to exactly one element of
maps to exactly one element of  . The initial spray of probabilities in
. The initial spray of probabilities in  along each direction
along each direction  is given by
is given by 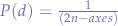 such that:
such that:
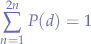
- handle each (2n-axes)-direction to the cumulative probability algorithm:
if(llList2String(dirs, itra) == "right") state right; if(llList2String(dirs, itra) == "up") state up; if(llList2String(dirs, itra) == "left") state left; if(llList2String(dirs, itra) == "down") state down; . . . For direction in (2n-axes) - drections: If direction is state, then: Jump to state.
- expand the jump table in the recomputing state
computeto include n-directions, similarly to the previous point:
if(nextState == "right") state right; if(nextState == "up") state up; if(nextState == "left") state left; if(nextState == "down") state down; . . . For direction in (2n-axes) - drections: Forall state in states: If next state is state then goto state
- extend the
thrustandanti-thrustsymmetrically to include the (2n-axes)-directions:
thrust: if(direction == "right") { llSetVelocity(<-ENGINE_SPEED,0,0>, TRUE); return; } if(direction == "up") { llSetVelocity(<0,ENGINE_SPEED,0>, TRUE); return; } if(direction == "left") { llSetVelocity(<ENGINE_SPEED,0,0>, TRUE); return; } if(direction == "down") { llSetVelocity(<0,-ENGINE_SPEED,0>, TRUE); return; } . . . For axis in 2n-axes: Apply forward velocity along axis. Return. anti-thrust: if(direction == "right") { llSetVelocity(<ENGINE_SPEED,0,0>, TRUE); return; } if(direction == "up") { llSetVelocity(<0,-ENGINE_SPEED,0>, TRUE); return; } if(direction == "left") { llSetVelocity(<-ENGINE_SPEED,0,0>, TRUE); return; } if(direction == "down") { llSetVelocity(<0,ENGINE_SPEED,0>, TRUE); return; } . . . For axes in 2n-axes: Apply backward velocity along axis. Return.
Generalized Great Wanderer Algorithm
- For all n-axes, 2n-directions or 2n-faces of the wanderer, do:
- Generate a bijection mapping states to probabilities so that all probabilities add up to 1:
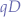 ->
-> and
and 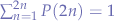 .
.
- Stable-sort both
QTandqDin descending order. - Jump to the first element in
qD. - Propulse object along that direction.
- If a collision is detected, then:
- Decrement P(n) in the
 probability set by a factor (increasing factor along each axis?).
probability set by a factor (increasing factor along each axis?).
- Goto 2.
For the contact, copyright, license, warranty and privacy terms for the usage of this website please see the contact, license, privacy, copyright.