Table of Contents
Motivation
llMoveToTarget implies a continuous dampening force that propels an object towards its destination. That got us thinking about simulating a typical artillery gun using simple physics free-fall mechanics motion equations. By creating an artillery gun, the whole simulation is entirely correct and does not rely on continuous applications of forces, such as dampening and propulsion.
Furthermore, this sort of artillery gun might be familiar to you from games such as Worms or Tank Wars where the objective is given to destroy the enemy artillery gun. In those games, the skill relies in intuitively guessing the velocity and angle at which a projectile must be fired in order to impact the target. The various scripts provided here perform all the calculations and there is no skill requirement. It is, of course, possible to implement an artillery firing game based on this script, but that is out of the scope of this article.
Background
The following section explains the general lines of free-fall mechanics that are implemented by the different artillery scripts.
Calculating the grid-distance
In order to calculate the distance between the artillery gun and the designated target avatar, we must factor out the elevation differential and then apply llVectDist to the two positional vectors. Formally, this is done like so:
float dΔ=llVecDist(<target.x,target.y,0>, <origin.x,origin.y,0>);
that is, the grid-distance  is given by the
is given by the 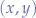 component differential between the target and the origin.
component differential between the target and the origin.
Calculating the Maximum Height of the Trajectory
From the basic motion equation, we have that:
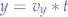
we know that the average vertical speed is half of the vertical speed:
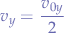
When the projectile reaches the apex of the flight path, its vertical speed will be 0. Makes sense no? If it has reached its maximum height, it will not have any upward speed anymore. We take thus the second equation and set  , thus:
, thus:

solving for  , we have:
, we have:
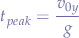
substituting in the basic motion equation, we obtain:
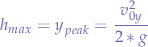
Calculating the Required Firing Angle Based on the Chosen Velocity
From the general motion equations, we have the  and
and  components:
components:
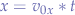
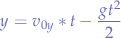
where  ,
, 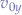 represent the velocity on the
represent the velocity on the  , respectively
, respectively  axis.
axis.  represents the time and
represents the time and  the linden gravitational force which is currently
the linden gravitational force which is currently 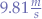 .
.
Since the fired projectile's flight path will be represented by a curve, we know that the total time of flight will be equal to twice the time at the peak. Thus, we have that:
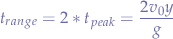
we substitute into the first equation and obtain the distance as:
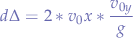
since  and
and  are vectors, we use the vectorial product and push it further to:
are vectors, we use the vectorial product and push it further to:
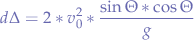
the trigonometric identity tells us that  , thus we finally obtain that the range equation is:
, thus we finally obtain that the range equation is:
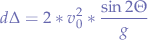
Now, we know the range  since we have already calculated it as the distance between the artillery gun and the designated target avatar. We also know g, the gravitational force since it is given by linden to be
since we have already calculated it as the distance between the artillery gun and the designated target avatar. We also know g, the gravitational force since it is given by linden to be 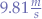 . The user is also prompted to choose the velocity v0, so we will know that too. This leaves us to extract the theta Θ angle which is required for the projectile to hit the target. In order to do that, we reverse the equation:
. The user is also prompted to choose the velocity v0, so we will know that too. This leaves us to extract the theta Θ angle which is required for the projectile to hit the target. In order to do that, we reverse the equation:
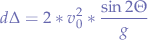
switching over the equal sign, we obtain:
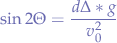
which means that:

thus,

Now, we know everything on the right hand side. By substituting all the parameters, we will obtain the first theta angle required to hit the designated target avatar (in my improvised terminology, the "Low" angle). To obtain the high angle, since it is complementary to 45 deg. secant, we simply subtract the theta "Low" angle from 90 degrees and careful to convert the obtained radian angles to degrees. Thus:
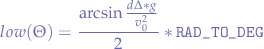
and

are the two possible angles required to hit the target. Why? Think about it intuitively, you can throw a projectile directly at a target, but you can also throw it towards the sky and wait for it to descend and hit the target as well. Thus, there are two possible angles at which you might throw a projectile. What's the difference? Well, it depends on your intentions.
Suppose that you have a gun and the you shoot towards some target. Now suppose that you have a resistance force on the projectile's firing direction and working in reverse. For example, there some wind source that tries to slow down your projectile. That wind force would alter the velocity of your bullet. However, a gun's blast power is greatly superior to whatever wind force may act against the bullet. Thus, it would not be necessary to chose the "High" angle - in fact, it would be intuitively a bad choice since friction will, in fact slow down the bullet given its small mass.
On the other hand, if you are a pirate and you want to sink a ship at a distance, given a heavy cannonball, you might want to chose the "High" angle and benefit from gravity to accelerate your projectile. I have not calculated the impact force in the script, however if you wish to do so:

where:
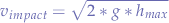
Which basically represents the kinetic force (given that mass is measured in lindograms, the force would be measured in lindograms-force) with which the projectile will impact the target. As you may observe, the impact force  exponentially increases with the velocity at impact and the mass of a projectile.
exponentially increases with the velocity at impact and the mass of a projectile.
For a bullet, the mass is small, the velocity great by contrast. For a pirate cannon, gunpowder wasn't able to deal too much of a velocity to a cannonball, however a cannonball was rather heavy so it benefited more from free-fall than from the induced velocity.
Can I always hit a target?
Nope. Of course not, since you might not have sufficient velocity. Here's formally why. Recall the two-theta angle:

The sinus function's value domain is between 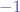 and
and 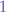 . That means, that
. That means, that 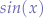 , for an arbitrary chosen x will give you a value that is between
, for an arbitrary chosen x will give you a value that is between 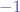 and
and 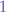 (inclusive).
(inclusive).
Whatever you plug as  into
into  , you will always get something that is in that range. Thus, if you take
, you will always get something that is in that range. Thus, if you take  , that means that if y is not between
, that means that if y is not between 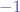 and
and 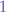 , then it is not in the domain of values of the sinus function and there is no possible angle at which the projectile can be fired in order to hit the target.
, then it is not in the domain of values of the sinus function and there is no possible angle at which the projectile can be fired in order to hit the target.
Intuitively (and hilariously), it's like saying, you only wear red, yellow and blue shoes. You are now wearing something green on your feet. However, via the hypothesis, since you only wear red, yellow and blue shoes, then that green stuff on your feet are not shoes.
Back to formalism, the domain of 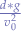 has to be in the range
has to be in the range ![Math $[-1,1]$](/lib/exe/fetch.php?media=wiki:latex:/img699628c77c65481a123e3649944c0d51.png) :
:
![Equation $$vdom(\frac{dΔ * g}{v_0^2}) = [-1, 1]$$](/lib/exe/fetch.php?media=wiki:latex:/img44023365fb140cb9a8ea391cc2567628.png)
in order for the projectile to hit the target.
Projectile Considerations
As mentioned previously, the larger and thus heavier the projectile, the heavier the impact. This is because the kinetic energy of the projectile is given by:
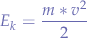
which means that the larger the velocity and the larger the mass of the object, the greater the resulting kinetic force will be - which is essentially what deals damage.
In Second Life terms, a good consideration would be to make the projectiles temporary so they will de-rez after a while.
Index
For the contact, copyright, license, warranty and privacy terms for the usage of this website please see the contact, license, privacy, copyright.