Table of Contents
Equation of an Elipse
![LaTeX
\begin{tikzpicture}
% grid
\draw[help lines] (-2,-2) grid (2,2);
% origin
\draw[red, line width=.1mm] (-0.1,-0.1) -- (0.1,0.1)
(0.1,-0.1) -- (-0.1,0.1);
\coordinate[label={[red]above left:$O$}] (O) at (0,0);
\draw (0,0) ellipse (20mm and 10mm);
\coordinate[label={[red]above left:$B$}] (B) at (0,1);
\drawpoint{B}{.5mm}{black}
\coordinate[label={[red]above right:$A$}] (A) at (2,0);
\drawpoint{A}{.5mm}{black}
\draw[black,dotted] (O) -- (A);
\draw[black,dotted] (O) -- (B);
\drawbrace{O}{A}{2mm}{blue}{$a$}{0}{-4mm}{mirror};
\drawbrace{O}{B}{2mm}{green}{$b$}{4mm}{0}{mirror};
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/imge584465f9f929f29e164ba05fd879bcd.png)
In standard form:
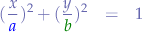
When  is not the centre of the ellipse, but rather an arbitrary point
is not the centre of the ellipse, but rather an arbitrary point 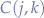 then:
then:
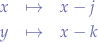
such that the equation becomes:
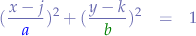
Equation of a Rotated Elipse
![LaTeX
\begin{tikzpicture}
% grid
\draw[help lines] (-2,-2) grid (2,2);
% origin
\draw[red, line width=.1mm] (-0.1,-0.1) -- (0.1,0.1)
(0.1,-0.1) -- (-0.1,0.1);
\coordinate[label={[red]below left:$O$}] (O) at (0,0);
\coordinate (X) at (5,0);
\draw[rotate=60] (0,0) ellipse (20mm and 10mm);
\coordinate[label={[red]above left:$B$}] (B) at (-.7,.8);
\drawpoint{B}{.5mm}{black}
\coordinate[label={[red]above right:$A$}] (A) at (1,1.7);
\drawpoint{A}{.5mm}{black}
\draw[black,dotted] (O) -- (A);
\draw[black,dotted] (O) -- (B);
\drawbrace{O}{A}{2mm}{blue}{$a$}{3mm}{-2mm}{mirror};
\drawbrace{O}{B}{2mm}{green}{$b$}{3mm}{3mm}{mirror};
% alpha
\markangle{O}{X}{A}{3mm}{3mm}{$\alpha$}{cyan}{north west}
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/imgd378df9c277eada4e337c3e51dc171b2.png)

Foci
![LaTeX
\begin{tikzpicture}
% grid
\draw[help lines] (-3,-3) grid (3,3);
% origin
\draw[red, line width=.1mm] (-0.1,-0.1) -- (0.1,0.1)
(0.1,-0.1) -- (-0.1,0.1);
\coordinate[label={[red]above left:$O$}] (O) at (0,0);
\draw (0,0) ellipse (30mm and 20mm);
\coordinate[label={[red]above left:$B$}] (B) at (0,2);
\drawpoint{B}{.5mm}{black}
\coordinate[label={[red]above right:$A$}] (A) at (3,0);
\drawpoint{A}{.5mm}{black}
\coordinate[label={[red]above left:$B'$}] (B') at (0,-2);
\drawpoint{B'}{.5mm}{black}
\coordinate[label={[red]above left:$A'$}] (A') at (-3,0);
\drawpoint{A'}{.5mm}{black}
\draw[black,dotted] (A) -- (O) -- (A');
\draw[black,dotted] (B) -- (O) -- (B');
\drawbrace{O}{A}{2mm}{blue}{$a$}{0}{-4mm}{mirror};
\drawbrace{O}{B}{2mm}{green}{$b$}{4mm}{0}{mirror};
\coordinate[label={[cyan]above:$F_{1}$}] (F_{1}) at ({sqrt(5}, 0);
\drawpoint{F_{1}}{.5mm}{cyan}
\coordinate[label={[cyan]above:$F_{2}$}] (F_{2}) at (-{sqrt(5}, 0);
\drawpoint{F_{2}}{.5mm}{cyan}
\coordinate[label={[cyan]above:$P$}] (P) at (-1, {sqrt(32/9)});
\drawpoint{P}{.5mm}{cyan}
\draw[cyan,dotted] (P) -- (F_{2});
\draw[cyan,dotted] (P) -- (F_{1});
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/imgfe128190a0b8dbf2302c62f8ede0e446.png)
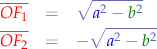

where  represents an arbitrary point on the ellipse perimeter.
represents an arbitrary point on the ellipse perimeter.
Area and Perimeter
![LaTeX
\begin{tikzpicture}
% grid
\draw[help lines] (-2,-2) grid (2,2);
% origin
\draw[red, line width=.1mm] (-0.1,-0.1) -- (0.1,0.1)
(0.1,-0.1) -- (-0.1,0.1);
\coordinate[label={[red]above left:$O$}] (O) at (0,0);
\draw (0,0) ellipse (20mm and 10mm);
\coordinate[label={[red]above left:$B$}] (B) at (0,1);
\drawpoint{B}{.5mm}{black}
\coordinate[label={[red]above right:$A$}] (A) at (2,0);
\drawpoint{A}{.5mm}{black}
\draw[black,dotted] (O) -- (A);
\draw[black,dotted] (O) -- (B);
\drawbrace{O}{A}{2mm}{blue}{$a$}{0}{-4mm}{mirror};
\drawbrace{O}{B}{2mm}{blue}{$b$}{4mm}{0}{mirror};
\coordinate[label={[red]above:$F$}] (F) at ({sqrt(2}, 0);
\drawpoint{F}{.5mm}{red}
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/img499c2d069cf8a6cbe82da9a03d337df8.png)
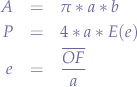
float wasElipseCircumference(float a, float b, integer precision) { float x = llListStatistics(LIST_STAT_MAX, [a, b]); float y = llListStatistics(LIST_STAT_MIN, [a, b]); float tol = llSqrt(llPow(.5, precision)); if (precision * y < tol * x) return 4 * x; float s = 0; float m = 1; while (x - y > tol * y) { x = .5 * (x + y); y = llSqrt(x * y); m *= 2; s += m * llPow(x - y, 2); } return PI * (llPow(a + b, 2) - s) / (x + y); }
fuss/mathematics/geometry/shapes/ellipses.txt · Last modified: by 127.0.0.1
For the contact, copyright, license, warranty and privacy terms for the usage of this website please see the contact, license, privacy, copyright.



