Table of Contents

Theory

This implementation is based on two former articles published by Wizardry and Steamworks:

Automata

\begin{tikzpicture}[->,>=stealth',shorten >=1pt,auto,node distance=2.8cm, semithick] \tikzstyle{every state}=[fill=red,draw=none,text=white] \node (z) at (6,2) {$z$}; \node (x) at (7,-2) {$x$}; \node (y) at (2,2.5) {$y$}; % z \draw [color=blue,dashed] (-2,-6) -- (z); % x \draw [color=orange,dashed] (-3,-2) -- (x); % y \draw [color=green,dashed] (2,-7) -- (y); \node[initial,state] (A) {$default$}; \node[state] (B) [below right of=A] {$compute$}; \node[state] (C) [above of=B] {$up$}; \node[state] (D) [above right of=B] {$forward$}; \node[state] (E) [right of=B] {$right$}; \node[state] (F) [below of=B] {$down$}; \node[state] (G) [below left of=B] {$backward$}; \node[state] (H) [left of=B] {$left$}; \path (A) edge node {1} (B) (B) edge node {$p_{u}$} (C) (C) edge node {1} (B) (B) edge node {$p_{f}$} (D) (D) edge node {1} (B) (B) edge node {$p_{r}$} (E) (E) edge node {1} (B) (B) edge node {$p_{d}$} (F) (F) edge node {1} (B) (B) edge node {$p_{b}$} (G) (G) edge node {1} (B) (B) edge node {$p_{l}$} (H) (H) edge node {1} (B); \end{tikzpicture}

Figure 1: The Great Wanderer uses an 8-state wNNA to determine the next traveling direction. The 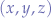$(x,y,z)$ Second Life corresponding local axes are superposed on the automaton for clarity and shows the trajectory determined by the wNNA.

As you can observe from Figure 1., the Great Wanderer uses the following states to navigate an enclosed space: 

default - this is the initial state.
forward - move the great wanderer forward.
backward - move the great wanderer backward.
left - move the great wanderer left.
right - move the great wanderer right.
up - move the great wanderer up.
down - move the great wanderer down.
compute - reserved for event protection.

The difference from our classic wNFA is that we do not consume states. Instead, they are re-used again, depending on the changes in probabilities for every movement: forward, backward, left, right, up and down. That makes it a Weighted Non-Deterministic Non-Finite Automaton (wNNA) rather, since the Great Wanderer never stops moving and hence never ends up in an end-state. This is on purpose because the Great Wanderer is not meant to stop moving at any point.

Furthermore, we ensure that we do not get stuck in some state by using a timer in each state: 

    timer() {
        llSetTimerEvent(0);
        if(llFabs(
          llVecMag(
            llList2Vector(
              llGetObjectDetails(llGetKey(), [OBJECT_VELOCITY]), 0))) 
                < ENGINE_SPEED/2) state compute;
        llSetTimerEvent(1);
    }

which ensures that in case the velocity of the Great Wanderer drops to less than half of the engine speed, the wNNA will immediately switch to the recompute state which will first decrement the probability of the current direction being chosen (since it got the Great Wanderer stuck in the first place) and then pick a new direction based on the current amended set of probabilities.

Formally, a wNNA is a reduction of a wNFA where the set of final accepting states is empty 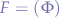$F=( \Phi )$. An extra condition is that all the probabilities have to add up to the same value at every transition of the automaton:

$P_{t} = p_{f} + p_{b} + p_{l} + p_{r} + p_{u} + p_{d}$

In other words, 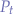$P_{t}$ must remain constant for all transitions of the wNNA (see Figure 1.). In this script, we have chosen probabilities in the range 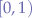$[0,1)$ for convenience.

Canceling Gravity

The default state is the main entry point, and used for initial set-up. In the default we set-up the counter-gravity by calling llSetBuoyancy with a parameter of 1. It might be (although it is unspecified), that in some cases llSetForce is inappropriate for countering gravity unless the distance between the Great Wanderer and the ground is taken into consideration. That is, when we tested llSetForce by calling: 

llSetForce(<0,0,9.81>*llGetMass(), FALSE);

we noticed undefined behavior. Our first tests, consisted in a physical primitive containing the aforementioned code, placed within a physical and hollow box which resulted in the upward force being larger than -G, resulting in some unexplained upward movement. Conversely, when not in an enclosed environment, the physical box manifested expected behavior. Because of that, we switched to llSetBuoyancy which, for now, results in the expected result.

As you can see from Figure 1., the default state switches directly to the compute state in order to calculate the next direction of movement. That is where we use llSetBuoyancy to cancel out all the gravity.

Simplified Algorithm

The movement of the Great Wanderer is given by the following algorithm:

  1. initially pick some direction d to move on based on the set of probabilities P.
  2. if there is a collision at some point on the trajectory given by the direction d
  3. lower the probability of that direction being chosen again by decrementing it and redistributing the remainder to the rest of the probabilities P evenly.
  4. random-cumulatively pick the next the direction d based on the amended set of probabilities P.
  5. move on the trajectory given by the new direction d.
  6. repeat at 2.