Table of Contents
Equation of a Sphere
![LaTeX
\begin{tikzpicture} % MERC
%% some definitions
\def\R{3} % sphere radius
\def\angEl{25} % elevation angle
\def\angAz{-100} % azimuth angle
\def\angPhiOne{-50} % longitude of point P
\def\angPhiTwo{-35} % longitude of point Q
\def\angBeta{33} % latitude of point P and Q
%% working planes
\pgfmathsetmacro\H{\R*cos(\angEl)} % distance to north pole
\LongitudePlane[xzplane]{\angEl}{\angAz}
\LongitudePlane[pzplane]{\angEl}{\angPhiOne}
\LongitudePlane[qzplane]{\angEl}{\angPhiTwo}
\LatitudePlane[equator]{\angEl}{0}
%% draw background sphere
\fill[ball color=grey!10] (0,0) circle (\R); % 3D lighting effect
%% characteristic points
\path[pzplane] (\angBeta:\R) coordinate [label={[black]above left:$P$}] (P);
\drawpoint{P}{.5mm}{black};
\coordinate [label={[black]above left:$O$}] (O) at (0,0);
\drawpoint{O}{.5mm}{black};
\path[pzplane] (\R,0) coordinate (PE);
\path[xzplane] (\R,0) coordinate (XE);
\path[pzplane] (\R,0) coordinate [label={[black]above right:$R$}] (R);
\drawpoint{R}{.5mm}{black};
\draw[dotted,black] (O) -- (R);
\drawbrace{O}{R}{2mm}{black}{$r$}{0}{-4mm}{mirror};
%% meridians and latitude circles
\DrawLatitudeCircle[\R]{0} % equator
%% draw lines and put labels
%\draw (-\R,-\H) -- (-\R,2*\R) (\R,-\H) -- (\R,2*\R);
\draw[->] (O) -- (P);
% z axis
\draw[->,dashed,blue] (O) -- +(0,1.5*\R) node[above] {$z$};
% x axis
\path[xzplane] (0:\R) node[below,red] {$x$} coordinate (x);
\draw[->,dashed,red] (O) -- (x);
% y axis
\path[pyplane] (0:\R) node[left,green!50] {$y$} coordinate (y);
\draw[->,dashed,green!50] (O) -- (y);
% projection P
\path[pzplane] (0.8*\R,0) coordinate [label={[black]above right:$Q$}] (Q);
\drawpoint{Q}{.5mm}{black};
\draw[->,dotted] (P) -- (Q);
%angles
\draw[pzplane,->,thin] (0:0.5*\R) to[bend right=15]
node[midway,right] {$\alpha$} (\angBeta:0.5*\R);
\draw[equator,->,thin] (\angAz:0.5*\R) to[bend right=30]
node[pos=0.4,below] {$\beta$} (\angPhiOne:0.5*\R);
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/img453a75f576910bb3a374e29d5bce7dba.png)
The segment  is created b the projection of P on
is created b the projection of P on  and is also the bisection of the rectangle described by
and is also the bisection of the rectangle described by  .
.  is a perpendicular projection on the x-axis and
is a perpendicular projection on the x-axis and  is a perpendicular projection on the
is a perpendicular projection on the  -axis.
-axis.
In the triangle between  and the x-axis:
and the x-axis:
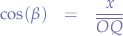
In the triangle between  and the y-axis:
and the y-axis:
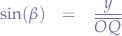
In the triangle given by 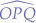 :
:

Now, we take the last equation:
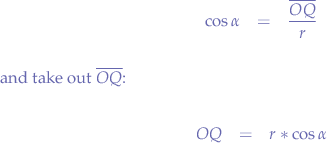
and substitute  in the first two equations:
in the first two equations:
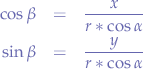
we extract x and y since it is what we are looking for:
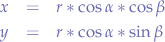
we also need z, so we go back to the triangle  :
:
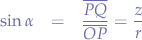
so we extract z:

Now, concluding, we obtain:
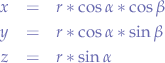
which is the parametric form of the equation of a sphere in space. If you follow what we did, we really did the same thing that we did for a sphere, but we just did it several times in order to obtain z as well.
Volume of a Sphere
![LaTeX
\begin{tikzpicture}
%% some definitions
\def\R{3} % sphere radius
\def\angEl{25} % elevation angle
\def\angAz{-100} % azimuth angle
\def\angPhiOne{-50} % longitude of point P
\def\angPhiTwo{-35} % longitude of point Q
\def\angBeta{33} % latitude of point P and Q
%% working planes
\pgfmathsetmacro\H{\R*cos(\angEl)} % distance to north pole
\LongitudePlane[xzplane]{\angEl}{\angAz}
\LongitudePlane[pzplane]{\angEl}{\angPhiOne}
\LongitudePlane[qzplane]{\angEl}{\angPhiTwo}
\LatitudePlane[equator]{\angEl}{0}
%% draw background sphere
\fill[ball color=grey!10] (0,0) circle (\R); % 3D lighting effect
% circles
\foreach \t in {-80,-60,...,80} { \DrawLatitudeCircle[\R]{\t} }
%\foreach \t in {-5,-35,...,-175} { \DrawLongitudeCircle[\R]{\t} }
% z axis
\draw[->,dashed,blue] (O) -- +(0,\R) node[above] {$z$} coordinate (z);
% x axis
\path[xzplane] (0:\R) node[below,red] {$x$} coordinate (x);
\draw[->,dashed,red] (O) -- (x);
% y axis
\path[pyplane] (0:\R) node[left,green!50] {$y$} coordinate (y);
\draw[->,dashed,green!50] (O) -- (y);
% Ox
%\drawbrace{O}{x}{2mm}{black}{$r$}{4mm}{0}{};
% Oy
%\drawbrace{O}{y}{2mm}{black}{$r$}{0}{4mm}{};
% Oz
%\drawbrace{O}{z}{2mm}{black}{$r$}{-4mm}{0}{};
% right-angle
%\node[square,minimum size=1mm, dotted] at (0.1,0.1) [draw,fill] (O) [magenta] {};
%\coordinate[label={[magenta]above right:$90^{\circ}$}] (90) at (0.2, 0.2);
\coordinate [label={[black]left:$O$}] (O) at (0,0);
\drawpoint{O}{.5mm}{black};
\path[pzplane] (\angBeta:\R) coordinate [label={[black]right:$P$}] (P);
\drawpoint{P}{.5mm}{black};
\draw[->,black] (O) -- (P);
\drawbrace{O}{P}{2mm}{black}{$r$}{0}{-4mm}{mirror};
\coordinate [label={[black]left:$Q$}] (Q) at (0,0.5*\R);
\drawpoint{Q}{.5mm}{black};
\draw[dotted] (P) -- (Q);
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/img47ac0a725508b537504c3417150759c1.png)
A sphere can be seen as infinitely many disks placed on top of each other, each representing the cross-section of the sphere at a certain point along the  axis.
axis.
This means that we can represent the difference in volume as a summation of all the surfaces of the circles (each having the area  ) aligned along the
) aligned along the  axis and write that:
axis and write that:

if we apply this to the whole range on the  axis while sweeping the dimension of the circles starting at the south and up to the north pole, in both cases where
axis while sweeping the dimension of the circles starting at the south and up to the north pole, in both cases where  . This makes the radius range from
. This makes the radius range from  at the south pole to
at the south pole to  at the north pole and the equation becomes:
at the north pole and the equation becomes:

At any given  , a right-angle triangle is formed by (for example)
, a right-angle triangle is formed by (for example)  in which we can apply Pythagoras. This translates to an universal right-angle triangle in point
in which we can apply Pythagoras. This translates to an universal right-angle triangle in point  so that at any value of
so that at any value of  we can map:
we can map:

and leading to Pythagoras:

Now we can replace  in the integral equation and obtain:
in the integral equation and obtain:

we can take out the constant  and rewrite the integral as:
and rewrite the integral as:

and expand using definite integral rules to:
![LaTeX
\begin{eqnarray*}
V &=& \pi*[\int_{-r}^{0}{r^{2}dz} - \int_{0}^{r}{z^{2}*dz}] & \\
&=& \pi*[ r^{2}z\biggr\rvert_{-r}^{0} - \frac{1}{3}z^{3}\biggr\rvert_{0}^{-r} ] & \\
&=& \pi*\{ (r^{2}*0) - (r^{2}*-r) - [ \frac{1}{3}(-r)^{3} - \frac{1}{3}(0)^{3} ]\} & \\
&=& \pi*( r^{3} + \frac{1}{3}*r^{3} ) & \\
&=& \pi*( \frac{3*r^{3} + r^{3}}{3} ) & \\
&=& \pi*( \frac{4*r^{3}}{3} )
\end{eqnarray*}](/lib/exe/fetch.php?media=wiki:latex:/img6844b8586080b381f1ad4938074dab2d.png)
and rearranging the terms nicely, we obtain the volume as:

Area of a Sphere
![LaTeX
\begin{tikzpicture}
%% some definitions
\def\R{3} % sphere radius
\def\angEl{25} % elevation angle
\def\angAz{-100} % azimuth angle
\def\angPhiOne{-50} % longitude of point P
\def\angPhiTwo{-35} % longitude of point Q
\def\angBeta{33} % latitude of point P and Q
%% working planes
\pgfmathsetmacro\H{\R*cos(\angEl)} % distance to north pole
\LongitudePlane[xzplane]{\angEl}{\angAz}
\LongitudePlane[pzplane]{\angEl}{\angPhiOne}
\LongitudePlane[qzplane]{\angEl}{\angPhiTwo}
\LatitudePlane[equator]{\angEl}{0}
%% draw background sphere
\fill[ball color=gray!10] (0,0) circle (\R); % 3D lighting effect
\fill[ball color=gray!75] (0,0) circle (0.75*\R); % 3D lighting effect
% circles
%\foreach \t in {-80,-60,...,80} { \DrawLatitudeCircle[\R]{\t} }
% z axis
\draw[->,dashed,blue] (O) -- +(0,\R) node[above] {$z$} coordinate (z);
% x axis
\path[xzplane] (0:\R) node[below,red] {$x$} coordinate (x);
\draw[->,dashed,red] (O) -- (x);
% y axis
\path[pyplane] (0:\R) node[left,green!50] {$y$} coordinate (y);
\draw[->,dashed,green!50] (O) -- (y);
% Ox
%\drawbrace{O}{x}{2mm}{black}{$r$}{4mm}{0}{};
% Oy
%\drawbrace{O}{y}{2mm}{black}{$r$}{0}{4mm}{};
% Oz
%\drawbrace{O}{z}{2mm}{black}{$r$}{-4mm}{0}{};
% right-angle
%\node[square,minimum size=1mm, dotted] at (0.1,0.1) [draw,fill] (O) [magenta] {};
%\coordinate[label={[magenta]above right:$90^{\circ}$}] (90) at (0.2, 0.2);
\coordinate [label={[black]left:$O$}] (O) at (0,0);
\drawpoint{O}{.5mm}{black};
\path[pzplane] (\angBeta:\R) coordinate [label={[black]right:$P$}] (P);
\drawpoint{P}{.5mm}{black};
\draw[->,black] (O) -- (P);
\drawbrace{O}{P}{2mm}{black}{$r$}{0}{-4mm}{mirror};
\coordinate [label={[black]left:$Q$}] (Q) at (0,0.5*\R);
\drawpoint{Q}{.5mm}{black};
\draw[dotted] (P) -- (Q);
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/img7ac1aa4126b65ce992324625bb7baad5.png)
The total volume inside a sphere of radius  can be thought of as the summation of the surface area
can be thought of as the summation of the surface area  of an infinite number of spherical shells of infinitesimal thickness concentrically stacked inside one another from radius
of an infinite number of spherical shells of infinitesimal thickness concentrically stacked inside one another from radius  to radius
to radius  .
.
At any given radius  the incremental volume
the incremental volume  equals the product of the surface area at radius
equals the product of the surface area at radius  and the thickness of the shell
and the thickness of the shell  .
.
Thus, we can write that:

as  approaches zero, we can integrate from
approaches zero, we can integrate from  to
to  (all the internal shells, from radius zero to the radius of the big sphere).
(all the internal shells, from radius zero to the radius of the big sphere).

We have already derived the volume, so we can now substitute the volume into the equation and rewrite:

Now we differentiate both sides of the equation with respect to  in order to get rid of the integral and derive the area
in order to get rid of the integral and derive the area  as a function of the radius
as a function of the radius  :
:
![Equations \begin{eqnarray*}
\frac{d}{dr}\biggr{[}\frac{4}{3}\pi*r^{3}\biggr{]} &=& \frac{d}{dr}\biggr{[}\int_{0}^{r}A(r)dr\biggr{]}
\end{eqnarray*}](/lib/exe/fetch.php?media=wiki:latex:/img5da0659cf6064b116e4eedb7e9ea80c2.png)
Differentiating on the left side, we obtain:
![Equations \begin{eqnarray*}
\frac{4}{3}\pi*3*r^{2} &=& \frac{d}{dr}\biggr{[}\int_{0}^{r}A(r)dr\biggr{]}
\end{eqnarray*}](/lib/exe/fetch.php?media=wiki:latex:/img1eda984cbed29b670bde9116744cb557.png)
while differentiating on the right side, the defined integral from  to
to  does not matter, we just use the differentiation integral rule:
does not matter, we just use the differentiation integral rule:
![Equations \begin{eqnarray*}
\frac{d}{d{\bf{x}}}\biggr{[}\int {\bf{x}}d{\bf{x}}\biggr{]} &=& {\bf{x}}
\end{eqnarray*}](/lib/exe/fetch.php?media=wiki:latex:/imgc76c87496567ee81c060ec2a427ef25a.png)
and obtain:

Finally, simplifying on the left side:

and turning the equality around so it looks like a forumula, yields the area of the sphere:

Since we already know that the area is a function of  , we can abbreviate this to:
, we can abbreviate this to:
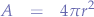
and obtain the final area of the large sphere.