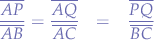Trigonometric Functions in Right-Angle Triangle

$\begin{tikzpicture} % grid \draw[help lines] (-2,-2) grid (2,2); % origin %\draw[red, line width=.1mm] (-0.1,-0.1) -- (0.1,0.1) % (0.1,-0.1) -- (-0.1,0.1); %\coordinate[label={[red]above:$O$}] (O) at (0,0); % coordinates \coordinate[label={[black]left:$A$}] (A) at (-1,1); \coordinate[label={[black]below:$B$}] (B) at (-1,-1); \coordinate[label={[black]right:$C$}] (C) at (1,-1); % triangle \draw[black, line width=.1mm] (A) -- (B) -- (C) -- cycle; % alpha \markangle{A}{B}{C}{3mm}{3mm}{$\alpha$}{cyan}{north} % braces %\drawbrace{B}{C}{2mm}{blue}{$a$}{0}{-4mm}{mirror} %\drawbrace{A}{B}{2mm}{green}{$c$}{-4mm}{0}{mirror} %\drawbrace{A}{C}{2mm}{red}{$b$}{3mm}{3mm}{} \end{tikzpicture}$

$\begin{eqnarray*} \sin{{\color{cyan}\alpha}} &=& \frac{\color{blue}{a}}{\color{red}{b}} = \frac{\overline{BC}}{\overline{AC}} & \\ \cos{{\color{cyan}\alpha}} &=& \frac{\color{green}{c}}{\color{red}{b}} = \frac{\overline{AB}}{\overline{AC}} & \\ \tan{{\color{cyan}\alpha}} &=& \frac{\color{blue}{a}}{\color{green}{c}} = \frac{\overline{BC}}{\overline{AB}} \end{eqnarray*}$

$\begin{eqnarray*} \csc{{\color{cyan}\alpha}} &=& \frac{\color{red}{b}}{\color{blue}{a}} = \frac{\overline{AC}}{\overline{BC}} & \\ \sec{{\color{cyan}\alpha}} &=& \frac{\color{red}{b}}{\color{green}{c}} = \frac{\overline{AC}}{\overline{AB}} & \\ \cot{{\color{cyan}\alpha}} &=& \frac{\color{green}{c}}{\color{blue}{a}} = \frac{\overline{AB}}{\overline{BC}} \end{eqnarray*}$

$\begin{eqnarray*} \tan{{\color{cyan}\alpha}} &=& \frac{\sin{{\color{cyan}\alpha}}}{\cos{{\color{cyan}\alpha}}} \end{eqnarray*}$

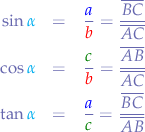
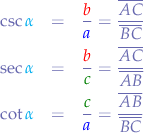
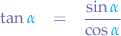
Pythagoras (Law of Cosines)

$\begin{tikzpicture} % grid \draw[help lines] (-2,-2) grid (2,2); % origin %\draw[red, line width=.1mm] (-0.1,-0.1) -- (0.1,0.1) % (0.1,-0.1) -- (-0.1,0.1); %\coordinate[label={[red]above:$O$}] (O) at (0,0); % coordinates \coordinate[label={[black]left:$A$}] (A) at (-1,1); \coordinate[label={[black]below:$B$}] (B) at (-1,-1); \coordinate[label={[black]right:$C$}] (C) at (1,0); % triangle \draw[black, line width=.1mm] (A) -- (B) -- (C) -- cycle; % alpha \markangle{A}{B}{C}{3mm}{3mm}{$\alpha$}{cyan}{north} % braces \drawbrace{B}{C}{2mm}{blue}{$a$}{0}{-4mm}{mirror} \drawbrace{A}{B}{2mm}{green}{$c$}{-4mm}{0}{mirror} \drawbrace{A}{C}{2mm}{red}{$b$}{3mm}{3mm}{} \end{tikzpicture}$

$\begin{eqnarray*} {\color{blue}a}^{2} &=& {\color{green}c}^{2} + {\color{red}b}^{2} - 2{\color{green}c}{\color{red}b}\cos{{\color{cyan}\alpha}} \end{eqnarray*}$

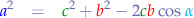
in a right-angle triangle, $\alpha=90^{\circ}$ such that $\cos{{\color{cyan}\alpha}}=0$ :

$\begin{eqnarray*} {\color{blue}a}^{2} &=& {\color{green}c}^{2} + {\color{red}b}^{2} \end{eqnarray*}$

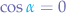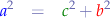
Medians in a Triangle

$\begin{tikzpicture} % grid \draw[help lines] (-5,-5) grid (5,5); % coordinates \coordinate[label={[black]left:$A$}] (A) at (-3,3); \coordinate[label={[black]below:$B$}] (B) at (-3,-3.5); \coordinate[label={[black]right:$C$}] (C) at (3,0); \coordinate[label={[black]above:$M_{a}$}] (Ma) at ($ (B) !.5! (C) $); \coordinate[label={[black]below left:$M_{b}$}] (Mb) at ($ (A) !.5! (C) $); \coordinate[label={[black]below right:$M_{c}$}] (Mc) at ($ (A) !.5! (B) $); % triangle \draw[black, line width=.1mm] (A) -- (B) -- (C) -- cycle; % median for a \path[draw, black, line width=.1mm, dotted, name path=median from A] (A) -- (Ma); % median for b \path[draw, black, line width=.1mm, dotted, name path=median from B] (B) -- (Mb); % median for c \path[draw, black, line width=.1mm, dotted, name path=median from C] (C) -- (Mc); % point \drawpoint{Ma}{.5mm}{black} \drawpoint{Mb}{.5mm}{black} \drawpoint{Mc}{.5mm}{black} % braces for segment medians a \drawbrace{B}{Ma}{3mm}{blue}{$a'$}{0}{-5mm}{mirror} \drawbrace{Ma}{C}{3mm}{blue}{$a''$}{0}{-5mm}{mirror} \drawbrace{B}{C}{14mm}{blue}{$a$}{8mm}{-14mm}{mirror} % braces for segment medians b \drawbrace{A}{Mb}{3mm}{red}{$b'$}{3mm}{5mm}{} \drawbrace{Mb}{C}{3mm}{red}{$b''$}{3mm}{5mm}{} \drawbrace{A}{C}{16mm}{red}{$b$}{8mm}{17mm}{} % braces for segment medians c \drawbrace{A}{Mc}{3mm}{green}{$c'$}{-5mm}{0}{mirror} \drawbrace{Mc}{B}{3mm}{green}{$c''$}{-5mm}{0}{mirror} \drawbrace{A}{B}{18mm}{green}{$c$}{-20mm}{0}{mirror} % median braces \drawbrace{A}{Ma}{1mm}{black}{$m_{a}$}{-2mm}{-2mm}{mirror} \drawbrace{B}{Mb}{1mm}{black}{$m_{b}$}{3.5mm}{-1mm}{mirror} \drawbrace{C}{Mc}{1mm}{black}{$m_{c}$}{0}{-3mm}{} % gravity centre \path[draw, red, name intersections={of=median from A and median from B, by=G}]; \drawpoint{G}{.5mm}{red} \coordinate[label={[black]above:$G$}] (G) at (G); \end{tikzpicture}$

$\begin{eqnarray*} m_{a} &=& \sqrt{\frac{2{\color{red}b}^{2}+2{\color{green}c}^{2}-{\color{blue}a}^{2}}{4}} \end{eqnarray*} \begin{eqnarray*} a' &\equiv& a'' & \\ b' &\equiv& b'' & \\ c' &\equiv& c'' \end{eqnarray*} \begin{eqnarray*} \frac{3}{4}({\color{blue}a}^{2} + {\color{red}b}^{2} + {\color{green}c}^{2}) &=& m_{{\color{blue}a}}^{2} + m_{{\color{red}b}}^{2} + m_{{\color{green}c}}^{2} \end{eqnarray*} \begin{itemize} \item $G$ represents the centre of mass also called the centroid. The entire weight of the triangle can be balanced in $G$ by pinning a pivot in $G$. \item The medians $m_{a}$, $m_{b}$ and $m_{c}$ divide the triangle $\widehat{ABC}$ into $6$ smaller triangles of equal surface. \end{itemize}$

Area of a Triangle

$\begin{tikzpicture} % grid \draw[help lines] (-2,-2) grid (2,2); % origin %\draw[red, line width=.1mm] (-0.1,-0.1) -- (0.1,0.1) % (0.1,-0.1) -- (-0.1,0.1); %\coordinate[label={[red]above:$O$}] (O) at (0,0); %\draw[black,line width=5mm] (-3, {3 * sqrt(3) - sqrt(3)}) -- ((-3,0); %\node [square,rotate={30},minimum size=10mm] at (-3, {3 * sqrt(3) - sqrt(3)}) [draw] (d2) [orange,fill,text=white] {$d_{2}$}; %\draw[orange,line width=.1mm] (-3, {3 * sqrt(3) - sqrt(3)}) -- (-2,0); %\draw[orange,line width=.1mm] (-3, {3 * sqrt(3) - sqrt(3)}) -- (0,2); % coordinates \coordinate[label={[black]left:$A$}] (A) at (-1,1.5); \coordinate[label={[black]left:$B$}] (B) at (-1.5,-1); \coordinate[label={[black]right:$C$}] (C) at (2,-1); \coordinate[label={[black]below:$P$}] (P) at (-1,-1); % mark P \drawpoint{P}{.5mm}{black} % triangle \draw[black, line width=.1mm] (A) -- (B) -- (C) -- cycle; % perpendicular \draw[black, line width=.1mm] (A) -- (P); % alpha \node [square,minimum size=1mm,dotted] at (-1.14,-0.85) [draw] (d2) [black] {}; % braces \drawbrace{B}{C}{2mm}{blue}{$a$}{0}{-4mm}{mirror} \drawbrace{A}{P}{2mm}{red}{$h$}{4mm}{0}{} \drawbrace{A}{B}{2mm}{green}{$c$}{-4mm}{0}{mirror} \drawbrace{A}{C}{2mm}{red}{$b$}{3mm}{3mm}{} \end{tikzpicture}$

$\begin{eqnarray*} A_{\widehat{ABC}} &=& \frac{{\color{red}h}{\color{blue}a}}{2} \end{eqnarray*}$

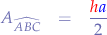
Using Heron's formula:

$\begin{eqnarray*} A_{\widehat{ABC}} &=& \sqrt{p(p-{\color{blue}a})(p-{\color{red}b})(p-{\color{green}c})} \text{ and } p=\frac{{\color{blue}{a}}+{\color{red}{b}}+{\color{green}{c}}}{2} \end{eqnarray*}$

A complete derivation of the Heron formula can be found in the mathematics section on triangles.

Theorem of Ceva

$\begin{tikzpicture} % grid \draw[help lines] (-2,-2.5) grid (2,2); % coordinates \coordinate[label={[black]left:$A$}] (A) at (-2,2); \coordinate[label={[black]below:$B$}] (B) at (-2,-2.5); \coordinate[label={[black]right:$C$}] (C) at (2,0); \coordinate[label={[black]above:$D$}] (D) at ($ (B) !.52! (C) $); \coordinate[label={[black]below left:$E$}] (E) at ($ (A) !.4! (C) $); \coordinate[label={[black]below right:$F$}] (F) at ($ (A) !.4! (B) $); % triangle \draw[black, line width=.1mm] (A) -- (B) -- (C) -- cycle; % line from a \path[draw, black, line width=.1mm, dotted, name path=line from A] (A) -- (D); % line from b \path[draw, black, line width=.1mm, dotted, name path=line from B] (B) -- (E); % line from c \path[draw, black, line width=.1mm, dotted, name path=line from C] (C) -- (F); % point \drawpoint{D}{.5mm}{black} \drawpoint{E}{.5mm}{black} \drawpoint{F}{.5mm}{black} % braces for segment medians a \drawbrace{A}{F}{3mm}{green}{$c$}{-5mm}{0}{mirror} \drawbrace{F}{B}{3mm}{green}{$c'$}{-5mm}{0}{mirror} % braces for segment medians b \drawbrace{B}{D}{3mm}{blue}{$a$}{3mm}{-5mm}{mirror} \drawbrace{D}{C}{3mm}{blue}{$a'$}{3mm}{-5mm}{mirror} % braces for segment medians c \drawbrace{C}{E}{3mm}{red}{$b$}{0}{5mm}{mirror} \drawbrace{E}{A}{3mm}{red}{$b'$}{0}{5mm}{mirror} % gravity centre \path[draw, red, name intersections={of=line from A and line from C, by=O}]; \drawpoint{O}{.5mm}{red} \coordinate[label={[black]above:$O$}] (O) at (O); \end{tikzpicture}$

$\begin{eqnarray*} \frac{{\color{green}c}}{{\color{green}c'}} * \frac{{\color{blue}a}}{{\color{blue}a'}} * \frac{{\color{red}b}}{{\color{red}b'}} &=& 1 \end{eqnarray*} The point $O$ represents the intersection of three arbitrarily drawn lines from the vertices ($A$, $B$ or $C$) of the triangle \widehat{ABC}.$

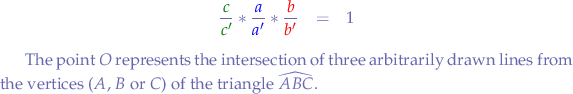
Theorem of Menelaus

$\begin{tikzpicture} % grid \draw[help lines] (-3,-3) grid (5,3); % coordinates \coordinate[label={[black]left:$A$}] (A) at (-2,2.5); \coordinate[label={[black]left:$B$}] (B) at (-2.5,-2); \coordinate[label={[black]right:$C$}] (C) at (3,-2); \coordinate[label={[black]south north:$P$}] (P) at ($ (A) !.3! (B) $); \drawpoint{P}{.5mm}{red} \coordinate[label={[black]south north:$Q$}] (Q) at ($ (A) !.7! (C) $); \drawpoint{Q}{.5mm}{red} \path[draw, black, line width=.1mm, dotted, name path=line from B] (B) -- (C) -- (3,-1); \draw[red, solid, line width=.1mm, name path=secant] (P) -- (Q) -- (4,-2); \draw[draw, red, name intersections={of=line from B and secant, by=R}]; \coordinate[label={[black]south north:$R$}] (R) at (4,-2); \drawpoint{R}{.5mm}{red} % triangle \draw[black, line width=.1mm] (A) -- (B) -- (C) -- cycle; % perpendicular %\draw[black, line width=.1mm] (A) -- (P); % braces \drawbrace{B}{R}{6mm}{blue}{$a$}{0}{-8mm}{mirror} \drawbrace{B}{C}{2mm}{blue}{$a'$}{0}{-4mm}{mirror} \drawbrace{C}{R}{2mm}{green}{$r$}{0}{-4mm}{mirror} \drawbrace{Q}{C}{2mm}{orange}{$s$}{-4mm}{-1mm}{mirror} \drawbrace{A}{Q}{2mm}{violet}{$t$}{4mm}{1mm}{} \drawbrace{A}{P}{2mm}{teal}{$u$}{-4mm}{0}{mirror} \drawbrace{P}{B}{2mm}{olive}{$v$}{-8mm}{0}{mirror} \end{tikzpicture}$

$\begin{eqnarray*} \frac{{\color{blue}a'}}{{\color{blue}a}}*\frac{{\color{orange}s}}{{\color{violet}}t}}*\frac{{\color{teal}u}}{{\color{olive}v}} &=& 1 \end{eqnarray*}$

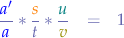
Theorem of Parallels

If $\overline{PQ}$ is parallel to $\overline{BC}$ then:

$\begin{eqnarray*} \frac{\overline{AP}}{\overline{AB}}=\frac{\overline{AQ}}{\overline{AC}}&=&\frac{\overline{PQ}}{\overline{BC}} \end{eqnarray*}$

Table of Contents