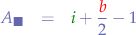Pick's Theorem
Given a lattice (a grid with equally disposed points), the following method can be used to measure the area of any given whole polygon.
![\begin{tikzpicture}
% grid
\draw[help lines,step=1] (-2,-2) grid (2,2);
% coordinates outer
\coordinate[label={[black]left:$A$}] (A) at (-1,1);
\coordinate[label={[black]below:$B$}] (B) at (-1,-1);
\coordinate[label={[black]right:$C$}] (C) at (1,-1);
\coordinate[label={[black]right:$D$}] (D) at (2,2);
% coordinate inner
\coordinate[label={[black]right:$E$}] (E) at (0,0);
\coordinate[label={[black]right:$F$}] (F) at (1,0);
\coordinate[label={[black]right:$G$}] (G) at (1,1);
\coordinate[label={[black]right:$H$}] (H) at (0,1);
% polygon
\draw[black, line width=.1mm] (A) -- (B) -- (C) -- (D) -- cycle;
% outer lattice points
\drawpoint{A}{1mm}{green}
\drawpoint{B}{1mm}{green}
\drawpoint{C}{1mm}{green}
\drawpoint{D}{1mm}{green}
% inner lattices points
\drawpoint{E}{1mm}{red}
\drawpoint{F}{1mm}{red}
\drawpoint{G}{1mm}{red}
\drawpoint{H}{1mm}{red}
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/img9b2d8c070208ffec4ef7977189f676c4.png "LaTeX")
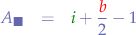
Given a lattice (a grid with equally disposed points), the following method can be used to measure the area of any given whole polygon.