Table of Contents

About

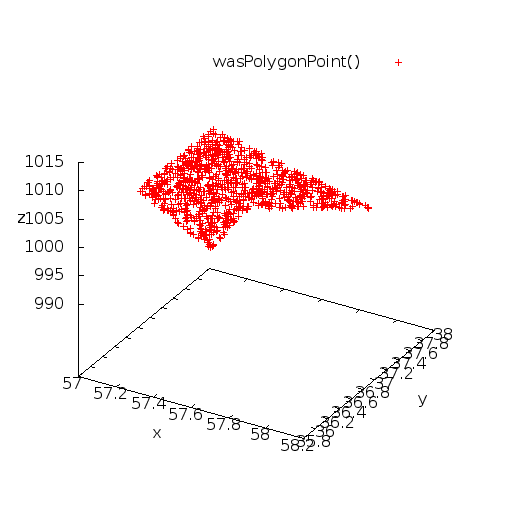
The following program is meant to create a primitive that will travel within a specified polygon (or, in civil engineering, a specified perimeter). This program works differently from other wanderer point generators because the polygon itself is strictly defined in the code - that is, the example below uses the following points that define a two-dimensional concave polygon: 

57.59832, 36.773457, 1004.033325
57.642971, 35.974648, 1004.033325
57.065857, 36.585957, 1004.033325
57.065857, 37.845955, 1004.033325
58.10437, 37.301346, 1004.033325

Uses

Different uses come to mind:

Graph

Video

Wanderer Algorithm

The algorithm is an accept-reject data sampling algorithm that first generates points within a circle circumscribing a polygon and then accepts all the points that fall within the polygon.

  1. First find the centroid from the polygon data points. This is called the smallest circle problem but we have made our own algorithm. For more details, please see the finding the centroid chapter below.
  2. The distance from the centroid to the point furthest away in the polygon data points can be used as a radius to circumscribe the polygon in a circle.
  3. Now, we can generate points within that circle by using wasCirclePoint.
  4. Using the PNPOLY (ray-cast) algorithm, we can now determine whether the points generated in that circle are also inside the polygon. So, generate a point within that circle using wasCirclePoint and then:
    1. If it is within the polygon, then that is a valid accepted point.
    2. If it is not within the polygon, then loop until we get a valid point.

The elegance of this algorithm is given by the fact that only the polygon points have to be known and that everything else is computed at run-time.

Shortcomings

For very nasty polygons with very acute angles, the circle circumscribing them will have a very large area compared to the area of the polygon. If this happens, then the algorithm slows down because the points generated within the encompassing circle will stand a low chance to also fall within the polygon.

A second ray-cast has to be performed to check whether the wanderer collides with a boundary. This is because the LSL code only generates points within a polygon which the wanderer then takes as the next destination. In doing so, the generated points using our algorithm do fall within the polygon but the movement of the wanderer may collide with the boundaries along the path between the current position and the next generated point. At first, we generate a point within the polygon: 

        moveTo(wasPolygonPoint(polygonPoints));

which makes sure to move the wanderer within the polygon and when the point is reached, then we generate the next point while also checking whether the path would intersect the boundaries: 

        moveTo(wasPolygonPath(llGetPos(), polygonPoints));

Finding the Centroid

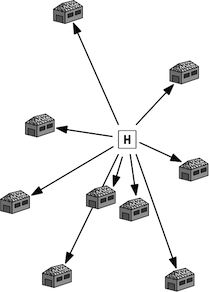
The centroid of a polygon - or rather, any set of points, is defined as a point that is placed within that data-set so that the distances from that point to all other points is minimal. You can visualize this the following way:

Suppose you have a scattering of houses on a field. You want to place a hospital (marked with H in the image) so that the hospital is placed at the minimal distance to all points. That means that some of the houses will reach the hospital faster, but that overall the distances from the houses to the hospital are minimal. This is illustrated by Marc van Kreveld in his computational geometry slides along with similar other problems.

Smallest Circle Algorithm

The most common way of finding the centroid from a data set of points, reduces to the smallest circle problem. The solution to the smallest circle problem is quite difficult (albeit clever) because it involves a lot of complication in drawing and moving circles. It is also not a definite algorithm - in the sense that it involves looping around until some condition is smaller than a calculated threshold which guarantees termination. Jacob Eliosoff and Richard Unger give a proof for this algorithm, demonstrating that the algorithm works and indicate that it is an 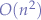$O(n^{2})$ algorithm.

Our Own Algorithm

We have chosen to create our own algorithm (see Zenos paradox on the race between Achilles and the Tortoise for inspiration) for finding the centroid, and we will illustrate it here:

  1. Given a set of points, select any point from the set and call it $P$.
  2. Calculate the distance from the selected point $P$ to all other points and select the longest distance.
  3. Move $P$ along the longest distance by $\frac{1}{2}$ of the distances length.
  4. Now loop at 2 and do the same, moving $P$ along the farthest distance by $\frac{1}{4},\frac{1}{8},\cdots,\frac{1}{2^{n}}$, every time decreasing how much to move along the longest distance, until the distance between the ideal centroid and the approximated centroid using this method falls within a user-specified threshold.

Series used for approximation: 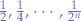$\frac{1}{2}, \frac{1}{4}, \cdots, \frac{1}{2^{n}}$ where $n \ge 1$ (absolutely convergent geometric series).

Similar to the Jacob Eliosoff and Richard Unger method the algorithm requires a threshold for termination. In our case, the threshold given by the user represents the distance between the ideal centroid and the centroid approximated by this algorithm.

Compared to the Jacob Eliosoff and Richard Unger method, our algorithm is "much much"™ simpler to implement since it just requires … division and addition.

Our algorithm performs an iterative refinement / approximation of the centroid such that upon every iteration, the position of the centroid is better estimated. In other words, iteration $n+1$ of our algorithm will provide a better estimation of the centroid than at iteration $n$. Given a desired precision (the upper threshold) our algorithm should have the same quadratic complexity $O(n^{2})$.

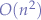In pseudocode: 

select any point p = p1 from p1,p2,...,pn
for i = 2 to m where m is a desired approximation
    // compute largest distance d from p to all other points p2,...,pn
    let d = 0
    let pm = p1
    for j=2 to n
        k = distance from p to pj
        if d < k
            set d = k
            set pm = pj
    // move point p
    move p towards pm by d / i
    let i = i * 2

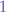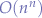The first complexity represents the algorithm runtime from $1$ to $n$ whilst the second is a repetitive complexity to determine the largest distance from the current point position to all other points thereby yielding $O(n^n)$ time complexity in total. Perhaps there is a way to eliminate the inner loop based on what is already known to achieve 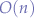$O(n)$ time complexity.

Proof

Hypothesis: when $n \mapsto \infty$ then the centroid will be found.

Perhaps a proof could be constructed inductively over the number of points.

One Point

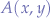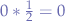For one point $A(x, y)$, the distance from $A$ to itself is $0$ such that all terms of the Zeno series $0 * \frac{1}{2} = 0$, $0 * \frac{1}{4}$, $\cdots$ reduce to zero and the centroid $C$ coincides with point $A$.

Two Points

For two points in space (defining a line): 

A (x1, y) ----------------------- B (x2, y)

Such that the centroid (midpoint, in 2D) is to be found at 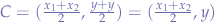$C = (\frac{x_{1}+x_{2}}{2}, \frac{y+y}{2}) = (\frac{x_{1}+x_{2}}{2}, y)$: 

A (x1, y) ------------x---------- B (x2, y)
                 C (x1+x2/2, y)

Note that the distance from $C$ to $A$ is equal to the distance from $C$ to $B$ such that any path can be chosen as a starting point (follows by applying the distance formula $d = \sqrt{(x_{2} - x_{1})^{2} + (y - y)^{2}} = x_{2} - x_{1}$ and substituting such that $CA = \frac{x_{1} + x_{2}}{2} - x_{1} = \frac{x_{1} + x_{2} - 2 * x_{1}}{2} = \frac{x_{2} - x_{1}}{2}$ and $CB = x_{2} - \frac{x_{1} + x_{2}}{2} = \frac{x_{2} - x_{1}}{2}$ 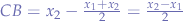resulting that $CB=CA=\frac{x_{2}-x_{1}}{2}$).

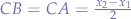Picking one of the two segments from $C$ to $A$ or $C$ to $B$, say $CA$, the first step is to move point $C$ (and rename to $Z$) by $d * \frac{1}{2}$ towards $A$ where $d$ represents the length of the segment $CA = \frac{x_{2}-x_{1}}{2}$: 

              Z ((3*x1+x2)/4, y)
A (x1, y) ------x-----x---------- B (x2, y)
                 C (x1+x2/2, y)

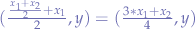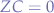$Z$ will thus have the coordinates $(\frac{\frac{x_{1} + x_{2}}{2} + x_{1}}{2}, y) = (\frac{3*x_{1} + x_{2}}{4}, y)$. From the next iteration on, the algorithm will always pick the segment $ZB$ since the segment $ZB$ will always be larger than segment $ZA$ until $ZC=0$ (in other words, when point $Z$ will coincide with point $C$; at which point $ZB=ZA$).

As we move the point $Z$ along the segment $ZB$ from $Z$ to $B$, we have to show that by applying the algorithm at every step we will eventually reach point $C$.

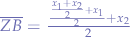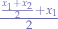First step, for going $\frac{1}{4} * \overline{ZB}$ from $Z$ to $B$, we compute $\overline{ZB} = \frac{\frac{\frac{x_{1} + x_{2}}{2} + x_{1}}{2} + x_{2}}{2}$ and knowing that $Z$ is at $\frac{\frac{x_{1} + x_{2}}{2} + x_{1}}{2}$ we obtain that:

$$ Z_{1/4} = \frac{\frac{x_{1} + x_{2}}{2} + x_{1}}{2} + \frac{1}{4} * \frac{\frac{\frac{x_{1} + x_{2}}{2} + x_{1}}{2} + x_{2}}{2} $$

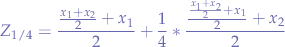
Further Ideas

Minimizing Reject Points

In the previous section we circumscribed the polygon into a minimal circle and then we would generate points within that circle later checking if the points also reside within the polygon. However, if we were to determine the minimal enclosing ellipse then the reject points could be further reduced.

In order to optimize the algorithm, the problem will shift to determining the minimal enclosing ellipse and then generating points within that ellipse and checking whether those points are within the polygon as well.

A polygon-point generator that uses an ellipse generator described in this section is now available on the ellipse polygon point generator page.

Probabilities

Measuring number distributions by observing where the wanderer tends to go? 

    +------+                 +------+
   /        \               /        \
  /   ->     +-------------+          \
 +    w                                +
  \          +-------------+          /
   \        /               \        /
    +------+                 +------+

Index