Magic Square Generation

A magic square is an arrangement of numbers in a square grid, where the numbers in each row, column, and the numbers on the big diagonals, all add up to the same number. We can determine that number. Suppose is the number that each row, column or big diagonal must add up to. Since there are rows, the sum of all the numbers in the magic square must be . Now, the numbers being added give the series 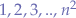, thus:

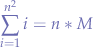
Knowing that:

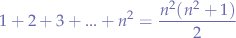
then it follows that:

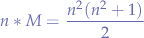
reducing, we obtain:

Thus, for a magic square, M=, for a magic square , for a magic square , etc…

1. Start in the middle column and place the number .
2. Go up and right and place .
   1. If you exceed the square bounds, wrap around and place .
   2. If you meet an occupied square, move down and place .
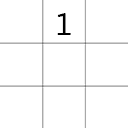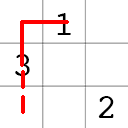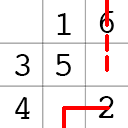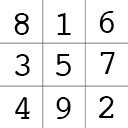
3. Repeat at 1 until all numbers are placed.

The same concept applies, for all counter-clockwise rotations of the movement direction, going back each time a square is occupied.

Every movement sequence will yield a magic square, all the columns, lines and big diagonals adding up to . The squares generated by all four sequences are:

The same applies to any odd square (with a central tile), although not all movements will necessarily build a magic square.

In this case, two of the paths do not generate magic squares. All the rest though do generate magic squares. The results in a case are the following squares:

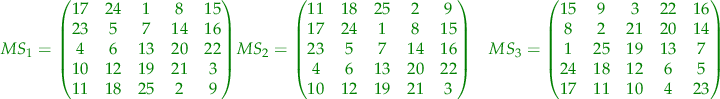
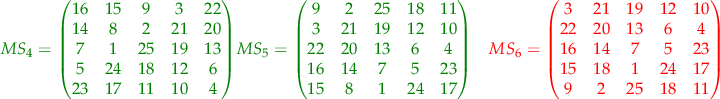
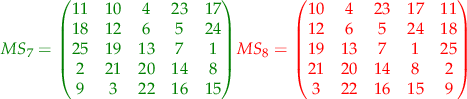
where the green squares are magic squares all the lines, columns and big diagonals adding up to while the red squares are not magic squares.