Table of Contents
Voltage Divider
Using two resistors  and
and 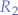 an input voltage
an input voltage 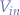 can be lowered to a resulting voltage
can be lowered to a resulting voltage  according to the formula:
according to the formula:
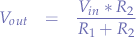
using the following circuit diagram:
* -------*
| |
| *
| \
| / R1
| \
+ * *
|
Vin *-------*
| | +
- * * *
| / Vout
| \ R2 *
| / | -
*--------*-------*
The equation has four parameters 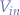 ,
,  ,
,  and
and  such that when three parameters are known, the fourth parameter can be obtained by solving the equation.
such that when three parameters are known, the fourth parameter can be obtained by solving the equation.
For ease-of-use, let  be the resistance that you pick and let
be the resistance that you pick and let  be the resistance you need to calculate after having picked the value for
be the resistance you need to calculate after having picked the value for 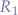 . The following steps convert the formula in order to solve for
. The following steps convert the formula in order to solve for 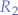 :
:
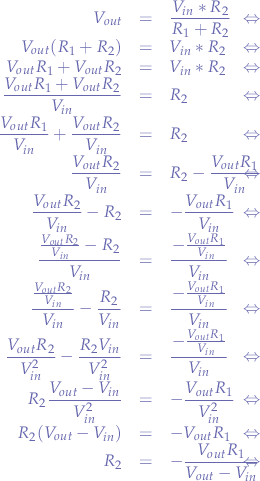
Counter-intuitively, the formula for 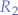 appears to result in a negative value but one has to bear in mind that
appears to result in a negative value but one has to bear in mind that  will always be smaller than
will always be smaller than 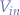 such that the result will always be negative and suppress the negative sign in front of the right-hand side of the equation.
such that the result will always be negative and suppress the negative sign in front of the right-hand side of the equation.
Autofire
Autofire is a game feature that allows the player to flick a hardware switch in order to make the game character shoot at the fastest possible rate thereby alleviating the player's need to mash the fire button repeatedly. Many (retro) consoles do not benefit from a built-in autofire switch. Alternative or addon controllers often had an autofire button.
On all consoles, the hardware buttons are no more than a momentary single press single throw (SPST) switch that closes a circuit and (usually) instructs the microprocessor to execute the corresponding action (ie: shoot).
As such, a circuit can be built using a NE555 timer that will rapidly make the connection between the two leads in parallel with the original hardware button.
For this mini-project, an astable circuit based on the NE555 timer is built:
Vcc
+
|
+--------------+-----+
| | |
R1 +---+-----+---+
| | 4 8 |
+----------+ 7 3 +------+ Vout
| | |
R2 | NE555 |
| | |
+----+-----+ 6 5 +------+
| | | 2 1 | |
| | +---+-----+---+ |
C1 | | | C2 = 10nF
| +---------+ | |
+--------------------+----------+
|
GND
where:
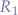 and
and 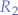 are resistors,
are resistors, and
and  are capacitors where
are capacitors where  is fixed at
is fixed at  ,
,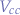 is the input voltage, and
is the input voltage, and is the output voltage that will fluctuate between high and low at the desired frequency,
is the output voltage that will fluctuate between high and low at the desired frequency, is ground.
is ground.
The formula to calculate the frequency at which the output voltage switches between high and low is given by:
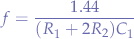
The period  is the time covered for one cycle, high and low:
is the time covered for one cycle, high and low:
T
|<--------->|
| |
| T1 T0 |
|<--->|<--->|
| | |
+-----+ +-----+
| | | |
| | | |
-----+ +-----+ +-----
where,  (the time
(the time  spends as high) is given by:
spends as high) is given by:
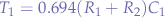
respectively  (the time
(the time  spends as low) is given by:
spends as low) is given by:

Empirically, a button press by a player on the hardware buttons has variable  and
and  and it does not matter whether the player spends more time with the button held down than with the button depressed when the player mashes the button.
and it does not matter whether the player spends more time with the button held down than with the button depressed when the player mashes the button.
Nevertheless, for simplicity, let us assume that the mark space ratio  , defined (as the ratio between the time that the button is being held down and the time that button is released):
, defined (as the ratio between the time that the button is being held down and the time that button is released):
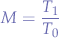
is equal to 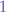 , meaning an equal time of the button being held down and released.
, meaning an equal time of the button being held down and released.
In this case, the mark space ratio will be  such that we can write
such that we can write  and substituting with the formulas for
and substituting with the formulas for  respectively
respectively  , we obtain:
, we obtain:
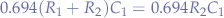
Let 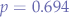 for simplicity and solving:
for simplicity and solving:
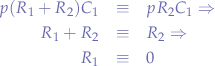
meaning that for a mark space ratio 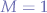 , the value of the resistor
, the value of the resistor 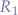 must be
must be  ; in other words, the
; in other words, the 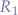 resistor is shorted (tersely, the wire itself will imply some resistance that will just be ignored).
resistor is shorted (tersely, the wire itself will imply some resistance that will just be ignored).
Pedantically, the period  should be equal to the CPU clock time because a higher frequency would simply not be perceived by the CPU however, the period
should be equal to the CPU clock time because a higher frequency would simply not be perceived by the CPU however, the period  could also be equal to the frames per second rating since a higher frequency could not be perceived on the screen.
could also be equal to the frames per second rating since a higher frequency could not be perceived on the screen.
In the end, various games accept different button mash speeds such that the period  could be chosen as any value close to the FPS. In this case, let
could be chosen as any value close to the FPS. In this case, let  (
( ) and
) and 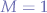 which would mean that the button will be pressed for
which would mean that the button will be pressed for  and then depressed for
and then depressed for 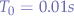 (
( ) and then pressed again, ...
) and then pressed again, ...
For 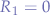 both equations for
both equations for  and
and  reduce to:
reduce to:
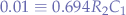
and solving for 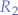 :
:

That is, taking values for the capacitor  we can obtain the necessary value for the resistor
we can obtain the necessary value for the resistor 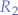 . For instance, taking a capacitor of
. For instance, taking a capacitor of 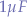 (
( ), the value for
), the value for 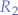 is obtained:
is obtained:
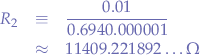
And, as it always is the case with engineering, nobody is going to produce a  resistor, just for you. One can plot
resistor, just for you. One can plot  vs
vs 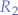 and select points on the curve in order to hopefully obtain practical values for
and select points on the curve in order to hopefully obtain practical values for  and
and 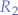 :
:
So, let's see: when 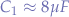 then
then  . Of course, were the values
. Of course, were the values  and
and 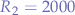 to be substituted in the original formulas,
to be substituted in the original formulas,  which is not exactly the initial goal of
which is not exactly the initial goal of  - but good enough to simulate a repeated button press!
- but good enough to simulate a repeated button press!
Consoles will definitely not mind variations of the order of milliseconds when it comes to button mashing however, if leeway is to be given, then 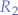 could perhaps be substituted by a variable resistor such that the period
could perhaps be substituted by a variable resistor such that the period  could become adjustable.
could become adjustable.
Transistor as a Switch
A 2N3904 BJT (base-junction transmitor) transistor can be used as a low-voltage switch in a circuit instead of a relay. The schematic is built around  which is the standard voltage used by most IoT devices.
which is the standard voltage used by most IoT devices.
The value of the base resistor 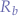 that must be used in order to run the transistor at saturation can be calculating. Let the following circuit be a guide for the calculations:
that must be used in order to run the transistor at saturation can be calculating. Let the following circuit be a guide for the calculations:
+--------+ Vcc
/
+------------------+ \
^ ^ | /
| | \ | | Ic
| Vb = Ib * Rb / Rb | v
| | \ Ib C
| | | -> |/
Vi v +---+---------B|\ hFE
| ^ E
| | Vbe |
| v |
+-----------------------------------+
|
- GND
We have an input voltage 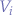 such as the
such as the  from a GPIO pin equal to the sum of the base-emitter voltage of the NPN transistor
from a GPIO pin equal to the sum of the base-emitter voltage of the NPN transistor 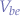 and the base voltage
and the base voltage 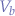 :
:

using Ohm's law, it is known that:

Substituting, the following relation is obtained:
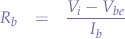
In order to guarantee that the transistor operates in the saturation region, the base current is multipled by a factor of  , such that:
, such that:
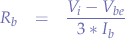
Also, knowing that BJT behave typically as a forward-biased diode with an approximate voltage drop of  , it is obtained that
, it is obtained that 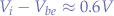 . Now, since the base-emitter voltage
. Now, since the base-emitter voltage 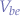 is usually negligible by comparison to the input voltage
is usually negligible by comparison to the input voltage 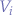 , the formula reduces to:
, the formula reduces to:
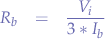
Finally, to determine  , the following relation is given:
, the following relation is given:
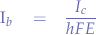
where  is the DC gain of the transistor and
is the DC gain of the transistor and  is the current flowing through the collector.
is the current flowing through the collector.
Substituting for 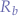 the following formula is obtained:
the following formula is obtained:
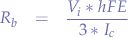
from where the value of the base resistor can be determined as a relation between the input voltage 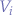 , the DC gain of the transistor (
, the DC gain of the transistor ( ) and the collector current
) and the collector current  (also the load current).
(also the load current).
As an example, let us assume that the device to be powered requires the load current 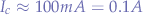 , that the device should be toggled from a GPIO pin capable of supplying
, that the device should be toggled from a GPIO pin capable of supplying  and that the DC gain of the transistor
and that the DC gain of the transistor 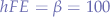 .
.
In that case the value of the base resistor 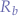 is:
is:
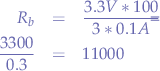
or  .
.
The value for the load  can be determined using the same schematic:
can be determined using the same schematic:
+--------+ Vcc
| Ql ^
/ |
+------------------+ \ Rl Vcc-Vce
^ ^ | / |
| | | | Ic | |
| | | v | v
| | \ +--------+
| Vb = Ib * Rb / Rb | ^
| | \ Ib C |
| | | -> |/ |
Vi v +---+---------B|\ hFE Vce
| ^ E |
| | Vbe | |
| v | v
+-----------------------------------+--------+
|
- GND
where:
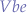 ,
,  and
and 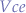 are all parameters that are given by the transistor specifications.
are all parameters that are given by the transistor specifications.
Knowing that every load has an internal resistance 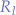 and applying Ohm's law in quadrant
and applying Ohm's law in quadrant  , the load current
, the load current  can be determined as:
can be determined as:

Example
Assume the following circuit:
+--------- S2 +----------+
| 3.3V |
- GND |
C
|/
+--- S1 +----+/\/+----B| 2N3904
| 0V 460kOhm |\
| E
- GND |
|
+ + (a) 864.7uV
+ - (b)
|
- GND
When the GPIO ( ) pin is pulled low, for instance, programatically by controlling the GPIO pin through software, the current flowing between the collector and emitter of the
) pin is pulled low, for instance, programatically by controlling the GPIO pin through software, the current flowing between the collector and emitter of the 2N3904 NPN BJT transistor is as low as 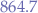 which is insufficient to power a device (connected to pins
which is insufficient to power a device (connected to pins  and
and  ).
).
+--------- S2 +----------+
| 3.3V |
- GND |
C
|/
+--- S1 +----+/\/+----B| 2N3904
| 3.3V Rb=460kOhm |\
| E
- GND |
|
+ + (a) 2.966V
+ - (b)
|
- GND
When the GPIO (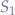 ) is pulled high, the BJT transistor will allow up to
) is pulled high, the BJT transistor will allow up to  to flow from
to flow from  through the collector and to the emitter thereby powering a device (connected to pins
through the collector and to the emitter thereby powering a device (connected to pins  and
and  ).
).
PCB Design
Given the required components consisting in just a resistor and a transistors, various PCB designs can made. Small modules can be created by using a 2N3904 transistor and an surface-mounted resistor using a dual-layer PCB. Larger modules would use a standard long resistor on the base but are still sufficiently small to serve most applications.
Shortcomings
The problem with the transistor switch is that the 2N3904 transistor will not allow a high amperage to flow through the junction such that the switch is best used to trigger digital buttons rather than act as a relay. Under no circumstance should a transistor switch be used to operate mains voltages (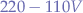 ) and apparatus that might require entire amperes of power. For the latter case, a reed relay such as the R1 series from Rayex Electronics should be used instead of a transistor switch.
) and apparatus that might require entire amperes of power. For the latter case, a reed relay such as the R1 series from Rayex Electronics should be used instead of a transistor switch.
RC Delay Circuit
An RC circuit delays the voltage between the two poles of the resistor.
Schematic:
(a) (b)
+----+/\/\/\+----+
R |
|
+
-----
----- C
+
|
|
+
GND
After a given time  the voltage
the voltage 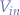 applied at pole (a) will be forwarded to point (b) as
applied at pole (a) will be forwarded to point (b) as  where
where 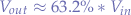 . The time
. The time  is computed as
is computed as  where
where  is the value (in Ohms) of the resistor and
is the value (in Ohms) of the resistor and  is the value (in Farrads) of the capacitor.
is the value (in Farrads) of the capacitor.
Example
The circuit will be:
(a) (b)
+----+/\/\/\+----+
R=10kΩ |
|
+
-----
----- C=100nF
+
|
|
+
GND
Assuming:
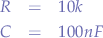
and applying 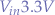 to the input pin (a), the time it will take for the voltage to propagate from (a) to (b) will be:
to the input pin (a), the time it will take for the voltage to propagate from (a) to (b) will be:
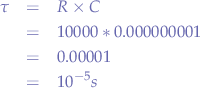
and the voltage obtained at  will be:
will be:
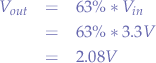
Incidentally, this is the circuit required (page 17, ESP32 Hardware Design Guidelines V1.9) to boot an Espressif ESP32 SoC where point (a) represents the 3.3V pin, point (b) represents the CHIP_PU (or EN, enable) pin and the ground can be leveraged from any pin on the ESP32 board.
Logic Level MOSFETs
MOSFETs are a type of transistors that are capable of switching a high amount of current with a relatively small switching current provided to the base of the transistor. Logic level MOSFETs commonly have an L in their description (ex: IRLZ44) indicating that the voltage provided to the base in order to switch the current between the emitter and collector is commonly between  and
and  .
.
In order to make sure that a transistor is a logic level transistor the RDS(on) ("Static Drain-to-Source On-Resistance") and the VGS(th) (Gate Threshold Voltage) values can be inspected on the datasheet.
Typically, logic level MOSFETs will have an RDS(on) value about  and lower and the
and lower and the VGS(th) value is usually also very small (ie: between  and
and  ). Regular MOSFETs on the other hand will have much higher thresholds.
). Regular MOSFETs on the other hand will have much higher thresholds.
Logic level MOSFETs also dissipate much less heat: knowing the voltage applied to the base as well as the expected switching current:
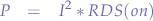
If the power in Watts is less than a quarter Watt, then more than likely a heatsink is not required.
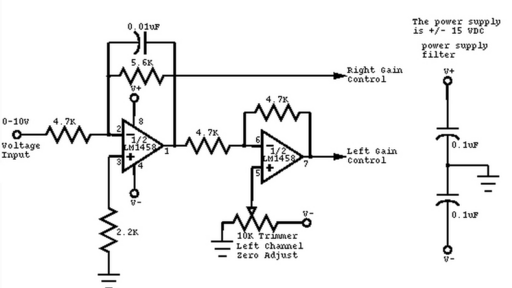
Mono to Stero Converter
An interesting mono-to-stereo converter based on two LM1458 amplifiers.
Estimating the Runtime of Equipment on Batteries
Using the formula:

where:
 stands for Watt-Hour,
stands for Watt-Hour, stands for Amperes-Hour and
stands for Amperes-Hour and  for voltage
for voltage
given a battery with a given  rating and a given voltage
rating and a given voltage  one can determine the Watt-Hours (
one can determine the Watt-Hours ( ) that the battery can provide. Dividing the Watt-Hours by the rating of the equipment in Watts (
) that the battery can provide. Dividing the Watt-Hours by the rating of the equipment in Watts ( ) leads to an approximation of time (measured in hours) that the battery will be able to run the equipment for.
) leads to an approximation of time (measured in hours) that the battery will be able to run the equipment for.
In other words:
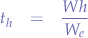
where:
 is the time measured in hours,
is the time measured in hours,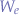 is the Watt rating of the equipment
is the Watt rating of the equipment
The formulas can then be combined conveniently by substituting and then solving for  :
:
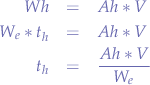
resulting in the final formula:
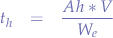
where:
- t_{h} is the time in hours that the battery will be able to run the equipment connected to the battery for,
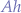 is the Amperes-Hours rating of the battery,
is the Amperes-Hours rating of the battery, is the Voltage rating of the battery (and the equipment),
is the Voltage rating of the battery (and the equipment),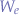 is the Watt rating of the equipment
is the Watt rating of the equipment
Note that many times the voltage has to be stepped or even direct current must be converted to alternative current such that in such cases the formulas would only apply at no-loss efficiency which is impossible. For instance, an inverter, a device that converts direct current to alternative current has a typical loss of  such that the loss has to be deducted from the result.
such that the loss has to be deducted from the result.
For a lead-acid car battery, if one would calculate that some equipment could be sustained for, say, 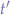 amount of hours, discharging a lead-acid car battery beyond
amount of hours, discharging a lead-acid car battery beyond  of its total charge would effectively mean killing the battery, such that a more realistic run time for the equipment would be half the calculated time, or, in other words
of its total charge would effectively mean killing the battery, such that a more realistic run time for the equipment would be half the calculated time, or, in other words 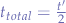 , after which the battery should be disconnected. In some sense, only half a lead-acid car battery calculated watt hours are useful, whilst the other half is necessary to keep the battery itself alive. This is much different with deep-discharge batteries such as
, after which the battery should be disconnected. In some sense, only half a lead-acid car battery calculated watt hours are useful, whilst the other half is necessary to keep the battery itself alive. This is much different with deep-discharge batteries such as LiFePO4 batteries that an be discharged to the full of their Watt-Hour capacity.
Flyback Diode for Relays
The following circuit can often been found in many cases where "relay modules" are sold:
Vcc
+-----------------+
a | +----------+ load
| |
+---------+ |
| | |
| +---|-----|---+ rl
| | 3 | |
| | 3 + |
^ | 3 L / |
D1 --- | 3 + |
| | 3 | |
| +---|-----|---+
| | |
+---------+ +----------+
|
|
-+- b
///
The purpose of the D1 diode is to provide a flyback circuit such that when a potential is established and then broken between the points  and
and  , the negative current created by inductor
, the negative current created by inductor  will not backflow and destroy any circuitry on the path between
will not backflow and destroy any circuitry on the path between  and
and  .
.
Transforming a Non-Latching Relay into a Latching Relay
The following sketch:
a
+-----------------+-----+
Vcc | |
| |
SWt \ |
+ |
| |
+---------+ |
| | |
| +---|-----|---+ RLY
| | 3 | |
| | 3 + |
| | 3 L / |
| | 3 + |
| | 3 | |
| +---|-----|---+
| | |
+---------------+-------+
| x |
| | |
+ | | load
SWr | | v
+ |
| |
| |
-+- b -+- c
/// ///
illustrates a circuit containing a non-latching relay  that has been transformed into a latching relay by connecting the relay inductor
that has been transformed into a latching relay by connecting the relay inductor  to the line that is supposed to carry the voltage load
to the line that is supposed to carry the voltage load 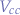 . One limitation of this circuit is that the coil voltage must equal the load voltage (which can be rare).
. One limitation of this circuit is that the coil voltage must equal the load voltage (which can be rare).
The switches  and
and  represent the trigger, respectively the reset switches that carry the functions of engaging the relay, when the trigger switch (
represent the trigger, respectively the reset switches that carry the functions of engaging the relay, when the trigger switch ( ) is engaged, respectively breaking the circuit when the reset switch (
) is engaged, respectively breaking the circuit when the reset switch ( ) switch is pressed.
) switch is pressed.
In order to understand the circuit, the load line is followed, between 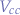 and
and  whilst paying attention to the state of the switches
whilst paying attention to the state of the switches  and
and  .
.
The following table will summarize the states of the switches, relative to the state of the switches but with the mention that the table should be read linearly as a sequence of states, from top to bottom, rather than an instantaneous display of states.
 |  | Outcome |
|---|---|---|
| depressed | depressed | With both switches depressed, the coil voltage is zero  , the load voltage is zero , the load voltage is zero 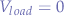 such that the circuit is off and cannot bear a load. such that the circuit is off and cannot bear a load. |
| depressed | pressed | With  depressed and depressed and  pressed, the coil voltage is zero ( pressed, the coil voltage is zero ( ) due to current not being able to flow neither between ) due to current not being able to flow neither between  and and  nor between nor between  and and  such that the circuit is off and cannot bear a load. such that the circuit is off and cannot bear a load. |
| pressed | pressed | With  held down and held down and  pressed, the coil voltage will be equal to pressed, the coil voltage will be equal to 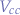 ( ( ) with current flowing between ) with current flowing between  and and  , the relay , the relay  will be engaged and current will flow between will be engaged and current will flow between  and and  such that the circuit will be on and capable of bearing a load. such that the circuit will be on and capable of bearing a load. |
| depressed | pressed | With  held down and now the switch held down and now the switch  released, a circuit is still formed between released, a circuit is still formed between  , ,  and and  (via junction (via junction  ) such that the circuit is on and can still bear a load. ) such that the circuit is on and can still bear a load. |
| depressed | depressed | Now, when  is released, the coil circuit between is released, the coil circuit between  and and  is broken, such that the relay is broken, such that the relay  decouples, and with the relay decoupled, the load circuit between decouples, and with the relay decoupled, the load circuit between  and and  is also broken, such that the circuit turns off and no load can be powered. is also broken, such that the circuit turns off and no load can be powered. |
The following video is a simulation using the circuit simulator at https://www.falstad.com/circuit/ of the latching relay circuit that follows the state changes described in the table and illustrates the latching functionality (the voltmeter is replaced by a LED):
Even though the theory (and even the simulation) are abstractions, it must be noted that in practice, the trigger switch  does not consist of a typical mechanical switch but more than likely be a mini-circuit itself (and perhaps even similar to the transistor switch), such that the "latching behaviour" that this circuit exhibits becomes more apparent and useful.
does not consist of a typical mechanical switch but more than likely be a mini-circuit itself (and perhaps even similar to the transistor switch), such that the "latching behaviour" that this circuit exhibits becomes more apparent and useful.
Arduino Controlled LED Light Strip
The following is a schematic for driving an LED light strip with 4 contacts (12V, R, G and B) using an Arduino. A  power source is used to power the Arduino via a step-down module to
power source is used to power the Arduino via a step-down module to  as well as the LED light strip via its
as well as the LED light strip via its 12V pin. The three R, G, B LED pins are controlled via three transistors having the emitter connected to the common ground (common with the step down and the power supply). The transistor act as latches, in this case, opening the feed of current from the R, G and B contacts to the ground. In doing so, each component red, green and blue is lit up and mix to form a desired color. In order to achieve the full spectrum of colors, the Arduino GPIO pins will output an analog signal (via the analogWrite function) in order to control the amount of current flowing from the collector connected to the component pins and to the ground. If the GPIO pins were to output a digital signal level, then only a few colors could be achieved since only toggling the R, G and B components on and off would be possible.
12V
+-------------------------+------------->
| |
+--+--+ +-----+-----+
| 12V | | 12V -> 5V |
+--+--+ +-----+-----+
| |
| | R
| +---------+ 5V | +--------->
| GND | |----+ |
+----------+ | /
| GPIO +------|+
| | \ e
| | v
| | |
| | GND
| Arduino | G
| | +--------->
| | |
| | /
| GPIO +------|+
| | \ e
| | v
| | |
| | GND
| | B
| | +--------->
| | |
| | /
| GPIO +------|+
| | \ e
| | v
| | |
+---------+ GND
Since the gate should be opened varying with the analog signal of the GPIO pins, the transistor type used is an NPN transistor. The actual model of the transistor depends greatly on how many LEDs are contained on an LED strip. Most projects involving this type of LED strip control use power-transitors that are capable of driving a large amount of LEDs however, even a general purpose 2N3904 transistor is capable of switching up to  from the collector to the emitter and carry between
from the collector to the emitter and carry between  to
to 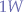 of power which may be sufficient for a smaller LED light strip depending on its power consumption.
of power which may be sufficient for a smaller LED light strip depending on its power consumption.
Reading a Remote Double-Relay Device with a Single Analog Input
The Chinese market produces some relatively-cheap miniature devices that consist in a radio receiver and two relays such that the relays can be controlled remotely with a remote control.
Given the two relays, the most straightforward usage for this device is to control two different appliances by directly connecting their power-lines to the relays on the controller and then use the remote to trigger one or the other.
The remote itself is simple enough, one LED and two buttons marked A and B. Pressing one or the other buttons will remotely couple either relay on the board and establish the connection between the pins marked COM1, respectively COM2 and ON1 respectively ON2 on the back of the device.
It becomes interesting to possibly read the device itself with an Arduino device in order to determine which of the two buttons on the remote control has been pressed. The straightforward solution would be to connect  to one side of the relay latch, then the other side to two different GPIO pins on the Arduino thereby using the two pins to determine which of the buttons has been remotely pressed. Nevertheless, as Arduino device go as as well as space-constrictions, it is even more interesting to use one single GPIO pin.
to one side of the relay latch, then the other side to two different GPIO pins on the Arduino thereby using the two pins to determine which of the buttons has been remotely pressed. Nevertheless, as Arduino device go as as well as space-constrictions, it is even more interesting to use one single GPIO pin.
The former illustration shows a schematic that uses a voltage divider in order to feed  when one remote button is pressed and then
when one remote button is pressed and then  when the other button is pressed whilst feeding the signal to an analog pin on the Arduino. The level on the analog GPIO pin can be read using the Arduino such that there are three distinct logical states that the remote control can find itself: no button pressed, button
when the other button is pressed whilst feeding the signal to an analog pin on the Arduino. The level on the analog GPIO pin can be read using the Arduino such that there are three distinct logical states that the remote control can find itself: no button pressed, button A pressed and button B pressed. In order to better understand this, here is the representation of the signal that ends up being read by the analog PIN on the Arduino.
^ V
|
| +-----------------------+ +-------------------- A (5V)
| | | |
| | | |
| | | +---------+. . . . . . . . . . . . B (3.4V)
| | | | | |
| | | | | |
+--+-----------------------+--+---------+--+---------------------> STANDBY (0V)
t
When the remote control is not used, no current flows through the relays such that the analog pin will be at 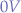 , when the
, when the B button is pressed, the current will flow through the voltage divider and reduce the  circuit voltage to
circuit voltage to  and finally when the
and finally when the A button is pressed, the current will flow straight-through from the  circuit voltage to the analog GPIO pin.
circuit voltage to the analog GPIO pin.
The same principle can be generalized in order to, perhaps have an array of relays and then keep dividing  using voltage dividers, such that an infinite number of relays and an infinite number of signals could theoretically be distinguished. However, for all practical purposes, the circuit just spares having to expend yet another pin on the Arduino.
using voltage dividers, such that an infinite number of relays and an infinite number of signals could theoretically be distinguished. However, for all practical purposes, the circuit just spares having to expend yet another pin on the Arduino.
Reversing the Polarity on a Single-Coil Latching Relay using a Remote Double-Relay
A remote double-relay is a module that can be found abundantly yet mostly in a format that contains two non-latching SPDT relays and sometimes a latching option might have been preferred. In order to solve the problem, a third latching relay can be added that will allow two circuits to be connected depending on which way the polarity is applied around the relay coil.
One good option for the latching relay is the G6S series of relays with a coil voltage of 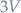 that suits most digital applications. One option is to just find a dual coil relay with its serial number reading
that suits most digital applications. One option is to just find a dual coil relay with its serial number reading G6SK because dual-coil relays do not need the polarity inverted but have a higher cost.
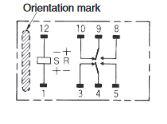
On the other hand, if only single coil relays are available, such as relays from the G6S series with the identifier reading G6SU, such coils must be toggled by reversing the polarity on the internal inductor within the coil. The following is a simple sketch from the top side of the coil internals:
As you can observe, the two pins closest to the mark labeled 1 and 12 correspond to the internal latching coil of the relay. Depending on whether positive or negative current is applied to either poles, the relay will switch current between the other pins meant to act as switches differently, with two modes being available whether pins 1 and 12 are positive or grounded.
An inconvenient problem that arises is that a circuit would have to somehow magically switch its polarity just to trigger the relay differently which is fairly counter-intuitive for a circuit where the positive and ground lanes have been established. However, with a remote-controlled double relay such as the pictured device, it is possible to achieve the inversion of polarity such that "A" and "B" buttons on the remote will map to either two states of the latching relay:
+------+-----+-------------------+
3V | |o |
+-----+-------------------+
\ |
+---+-----+ |
| |
| +--|---------+
--- | | 3
/// | | 3 Latching Relay
| | 3
+--|---------+
+---+-----+ |
| \ |
| +-----+-------------------+
| |o |
+------+-----+-------------------+
3V | |
|
---
///
The two relays on the left represent the non-latching relays of the remote control where each relay connects to one side when either "A" or "B" buttons are depressed.
- In this case, the closed state of both relays (when the remote control is left alone) both keep the coil pins of the latching relay pulled high which carries no meaning such that the latching relay does not commute from its current state.
- When button "A" is pressed (say, corresponding to the top-left-most relay on the schematic), the switch commutes and the common pin of the relay (center pin) connects via the relay to ground. However, the bottom-left-most relay is not affected by button "A", such that given the circuit, the other side of the latching relay will be pulled high (3V) thereby generating one state.
- When button "B" is pressed corresponding to the relay on the bottom-left-most side of the schematic, the current positive connection is broken (3V) and a connection to ground is made. Additionally, because button "B" does not affect the top-left-most relay on the schematic, the other side of the latching relay will be pulled high (3V) thereby generating one more state.
The "intelligent" part here is connecting both common and the connected pin of both relays together to 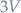 and to the coil pin of the relay on both sides such that pressing either button on the remote disconnects either side of the remote controlled relay thereby switching the polarity on the pins of the latching relay.
and to the coil pin of the relay on both sides such that pressing either button on the remote disconnects either side of the remote controlled relay thereby switching the polarity on the pins of the latching relay.
It should be possible to achieve the same effect using diodes and preventing current backflow, but the less components the better!
Antenna Length
The optimal length 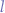 in meters for an antenna designed to receive signals with a frequency of
in meters for an antenna designed to receive signals with a frequency of  is given by the formula:
is given by the formula:
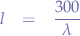
where  is the approximate speed of light in vacuum simplified to match the frequency in megahertz.
is the approximate speed of light in vacuum simplified to match the frequency in megahertz.
For instance, for a  signal, the optimal length will be:
signal, the optimal length will be:

However, since the wavelength can be represented as a sine function, any multiple of 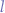 will still be able to pick up the signal efficiently.
will still be able to pick up the signal efficiently.
LED Candle
One very easy way to make a candle or a lighting source is to sticky-tape several LEDs to a button battery. LEDs typically take lower voltages like  or
or  but the standard large LEDs that seem to be the most common will tolerate
but the standard large LEDs that seem to be the most common will tolerate 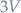 without issues.
without issues.
Capacitive Low-Pass Circuit for Alternative Current
Sensitive currents need a perfect input voltage that does not contain any jitter or current ripple. Looking back at LM voltage regulators, such as the ones used in various projects, like the HAM radio antenna audio injector, the circuit always contains two capacitors on both input and output lines. These capacitors are responsible for regulating current ripple, namely the current jitter on top of the main signal that degrades the shape of the signal itself.
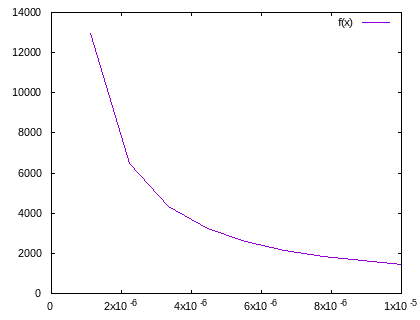
The following is a measurement of the input voltage to a power supply showing the  oscillation of the typical household voltage without any sort of filtering.
oscillation of the typical household voltage without any sort of filtering.
As can be noticed, the signal looks like it has "a bunch of hair on it" and that is precisely what an EMI filter will try to remove from the AC line. By contrast, the same measurement is carried out after attaching an A.C. line filter.
Which by contrast is a gorgeous signal.
The schematic for the attached filter as follows and consists in just a resistor and a capacitor that is placed on the A.C. line right before the rest of the power supply.
to transformer, rectifier,filter and regulator +----------+----------------+---------+ +------> ^ | | . \ | . AC / ----- . 220V \ R ----- C . / | v | | +----------+----------------+---------+
This is a capacitive low-pass filter such that it will only allow frequencies below a certain threshold to pass from the A.C. line to the rest of the power supply. The formula for calculating the cutoff frequency for the filter is the following:

where:
 is the value of the resistor in Ohms,
is the value of the resistor in Ohms, is the value of the capacitor in Farrads
is the value of the capacitor in Farrads
The capacitor, also called a decoupling capacitor, is what does most of the work and is kept low enough with a minimal amount of capacitance to short out the noise. For example, good values for the capacitor are below  . With that value picked, it is now possible to work out a good resistor, by solving for
. With that value picked, it is now possible to work out a good resistor, by solving for  :
:

and then substituting with numeric values by assuming that the line frequency is  , which is the standard in many jurisdictions:
, which is the standard in many jurisdictions:

which means that the value for the resistor should be about  .
.
Thinking about it, this is impressive; so much ripple on the signal that would pollute the inner-working of the components has been eliminated by just one single capacitor and a throwaway resistor! \
Given the simplicity of this circuit, these low-pass filters for A.C. current are extremely popular and can be found in various forms. For example, if you were to disassemble a standard PC power supply, in particular ones that are not extremely expensive, you will notice that a low-pass filter as described is placed behind the kettle cable socket on the inside of the power supply.
The capacitor is just soldered onto the pins of the kettle cable connector. Also, looking closer, a resistor can be observed across the bottom part of the capacitor. Both of these together constitute the circuit mentioned above. Power supplies like these are normally produced in mass and sometimes, depending on which jurisdiction they are shipped to, they must be adapted to ensure that they have the required parameters. For instance, different countries enforce different levels of RF noise. It might be the case that this power supply has been adjusted in post-processing and the filter added in order to reduce the EMI / RFI in order to meet requirements.
USB Charging Protocol
Traditionally, the USB 2.0 specification states that the delivered electricity should conform to  and
and  and USB 3.1
and USB 3.1  at
at  . For that reason, more power-hungry devices cannot be powered from a single USB port like CD-ROM drives or 3.5" hard-drives. However, the details mentioned are only meant when the USB port is operated together with a device and not as an USB charger.
. For that reason, more power-hungry devices cannot be powered from a single USB port like CD-ROM drives or 3.5" hard-drives. However, the details mentioned are only meant when the USB port is operated together with a device and not as an USB charger.
The BC1.2 charging specification allows between  and
and  to be provided to the device via an USB port, where the maximum current
to be provided to the device via an USB port, where the maximum current  can be provided in either CDP or DCP mode, both of which are charging mode with the distinction that CDP allows communication over the data lines.
can be provided in either CDP or DCP mode, both of which are charging mode with the distinction that CDP allows communication over the data lines.
DCP (Direct-Charging Protocol), on the other hand is made only for charging the battery and it is a protocol between a device and the charger that establishes the amount of current that can be drawn from the USB charger. The protocol is as follows:
+---------+ +---------+
| device | | charger |
+----+----+ +----+----+
| 0.6V on D(+) |
+------------------------------------->|
| |
| D(-):SDP <0.3V, charging >0.3V <0.8V |
|<-------------------------------------+
| |
| 0.6V on D(-) |
+------------------------------------->|
| |
| D(+):CDP <0.3V, DCP >0.3V <0.8 | |
|<-------------------------------------+
That is:
- the device sends a
 signal on its
signal on its D+line and measures theD-line during a first stage, - the second test distinguishes between
CDPorDCPmode.
The USB BC1.2 Specification and the Chinese Telecommunications Industry Standard YD/T 1591-2009 define that the D+ and D– data lines must be shorted together with a maximum series impedance of  in order to signal to the device that the charger is a DCP charger. Here is the schematic that would accomplish that:
in order to signal to the device that the charger is a DCP charger. Here is the schematic that would accomplish that:
+-----+
| USB +----------+ <-- 5V
| prt |
| |
| |
| +---+
| | \
| | / R200
| | \
| +---+
| |
| |
| |
| +---------+
+-----+ |
|
----- GND
////
Note that the word "maximum" is meaningful in the definition because looking at the BC1.2 protocol, during both the first and second phase of the device probe, if the current is passed directly between the data pins, then the charger would appear to the device as a DCP charger because in both test phases the  signal would just pass directly and will always fall between
signal would just pass directly and will always fall between  and
and  .
.
For the contact, copyright, license, warranty and privacy terms for the usage of this website please see the contact, license, privacy, copyright.