Table of Contents
Cross Product
The result of the cross-product of a two vectors is another vector. Given two vectors 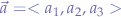 and
and 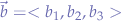 , their cross-product can be written as:
, their cross-product can be written as:
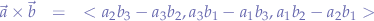
or, using determinants:
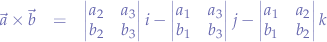
which is derived from:
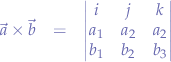
Properties
- The length of the resulting vector representing the cross-product of two vectors is:

where the vertical bars represent the scalar value of the vector.
- The length of the cross-product of two vectors is equal to the area of the parallelogram determined by the two vectors.
![LaTeX
\begin{tikzpicture}
% grid
\draw[help lines] (-3,-2) grid (4,2);
% origin
%\draw[red, line width=.1mm] (-0.1,-0.1) -- (0.1,0.1)
% (0.1,-0.1) -- (-0.1,0.1);
%\coordinate[label={[red]above:$O$}] (O) at (0,0);
%\draw[black,line width=5mm] (-3, {3 * sqrt(3) - sqrt(3)}) -- ((-3,0);
%\node [square,rotate={30},minimum size=10mm] at (-3, {3 * sqrt(3) - sqrt(3)}) [draw] (d2) [orange,fill,text=white] {$d_{2}$};
%\draw[orange,line width=.1mm] (-3, {3 * sqrt(3) - sqrt(3)}) -- (-2,0);
%\draw[orange,line width=.1mm] (-3, {3 * sqrt(3) - sqrt(3)}) -- (0,2);
% coordinates
\coordinate[label={[black]left:$A$}] (A) at (-1,1.5);
\coordinate[label={[black]left:$B$}] (B) at (-2,-1);
\coordinate[label={[black]right:$C$}] (C) at (2,-1);
\coordinate[label={[black]right:$D$}] (D) at (3,1.5);
\coordinate[label={[black]below:$P$}] (P) at (-1,-1);
% mark P
\drawpoint{P}{.5mm}{black}
% theta
\markangle{B}{A}{C}{2mm}{2mm}{$\theta$}{green}{south west}
% triangle
\draw[black, line width=.1mm] (A) -- (B) -- (C) -- (D) -- cycle;
% perpendicular
\draw[black, line width=.1mm] (A) -- (P);
% alpha
\node [square,minimum size=1mm,dotted] at (-1.14,-0.85) [draw] (d2) [black] {};
% braces
%\drawbrace{B}{C}{2mm}{blue}{$a$}{0}{-4mm}{mirror}
%\drawbrace{A}{P}{2mm}{red}{$h$}{4mm}{0}{}
%\drawbrace{A}{B}{2mm}{green}{$c$}{-4mm}{0}{mirror}
%\drawbrace{A}{C}{2mm}{red}{$b$}{3mm}{3mm}{}
\drawbrace{A}{P}{2mm}{black}{${\color{cyan}|\vec{b}|}\sin{\color{green}{\theta}}$}{10mm}{0mm}{}
\drawbrace{B}{C}{2mm}{blue}{$|\vec{a}|$}{0}{-4mm}{mirror}
\drawbrace{A}{B}{2mm}{cyan}{$|\vec{b}|$}{-6mm}{2mm}{mirror}
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/img5b4845586834d7e55f1735dc88b01f73.png)
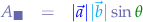
- Multiplication by scalars is commutative. For example, suppose that
 is a scalar and that
is a scalar and that 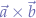 is the cross product of
is the cross product of  respectively
respectively  , in that case we have that:
, in that case we have that:

- The cross-product is distributive.

- The volume of the parallelepiped determined by the vectors
 ,
,  and
and  is equal to the magnitude of their scalar triple product.
is equal to the magnitude of their scalar triple product.
- The vector triple product of the vectors
 ,
,  and
and  is given by:
is given by:

- Two vectors are parallel if and only if their cross product is the zero vector.
Determining Triangle Area in Three Dimensions
One solution to find the area of a triangle is to determine its height and then proceed to the multiply the height by the base and divide by two. However, that may be a difficult task and instead, by using the parallelogram property of vectors, one can calculate the area of the parallelogram and then divide the area by two.
For the contact, copyright, license, warranty and privacy terms for the usage of this website please see the contact, license, privacy, copyright.



