Intersection Between Two Segments Given Four Points

$\begin{tikzpicture} % grid \draw[help lines] (-2,-2) grid (2,2); % origin \draw[black, line width=.1mm] (-0.1,-0.1) -- (0.1,0.1) (0.1,-0.1) -- (-0.1,0.1); \coordinate[label={[black]below left:$O$}] (O) at (0,0); \coordinate[label={[cyan]above left:$A$}] (A) at (-2,0); \drawpoint{A}{.5mm}{cyan} \coordinate[label={[blue]above left:$B$}] (B) at (2,1); \drawpoint{B}{.5mm}{blue} \coordinate[label={[green]above left:$C$}] (C) at (-1,1); \drawpoint{C}{.5mm}{green} \coordinate[label={[brown]above right:$D$}] (D) at (2,-1); \drawpoint{D}{.5mm}{brown} \draw (A) -- (B); \draw (C) -- (D); % median for A \path[draw, black, line width=.1mm, solid, name path=median from A] (A) -- (B); % median for B \path[draw, black, line width=.1mm, solid, name path=median from C] (C) -- (D); % gravity centre \path[draw, red, name intersections={of=median from A and median from C, by=I}]; \drawpoint{I}{.5mm}{red} \coordinate[label={[red]above:$I$}] (I) at (I); %\coordinate (C) at (2,0); %\coordinate (D) at (0,1); %\draw[dotted,->] (O) -- (C) node[below] {$x$}; %\draw[dotted,->] (O) -- (D) node[left] {$y$}; %\markangle{A}{B}{C}{3mm}{3mm}{$\alpha$}{cyan}{north} \end{tikzpicture}$

Given four points with known coordinates:

$\begin{eqnarray*} {\color{cyan}A} &=& A({\color{cyan}a_{1}}, {\color{cyan}a_{2}}, {\color{cyan}a_{3}}) \\ {\color{blue}B} &=& B({\color{blue}b_{1}}, {\color{blue}b_{2}}, {\color{blue}b_{3}}) \\ {\color{green}C} &=& C({\color{green}c_{1}}, {\color{green}c_{2}}, {\color{green}c_{3}}) \\ {\color{brown}D} &=& D({\color{brown}d_{1}}, {\color{brown}d_{2}}, {\color{brown}d_{3}}) \end{eqnarray*}$

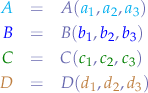
Writing the parametric equation for the line $\overline{AB}$ :

$\begin{eqnarray*} {\color{cyan}A} + t({\color{blue}B}-{\color{cyan}A}) &=& \begin{pmatrix} {\color{cyan}a_{1}} \\ {\color{cyan}a_{2}} \\ {\color{cyan}a_{3}} \end{pmatrix} + t\begin{pmatrix} {\color{blue}b_{1}} - {\color{cyan}a_{1}} \\ {\color{blue}b_{2}} - {\color{cyan}a_{2}} \\ {\color{blue}b_{3}} - {\color{cyan}a_{3}} \end{pmatrix} \end{eqnarray*}$

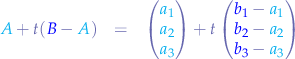
and the parametric equation for the line $\overline{CD}$ :

$\begin{eqnarray*} {\color{green}C} + t({\color{brown}D}-{\color{green}C}) &=& \begin{pmatrix} {\color{green}c_{1}} \\ {\color{green}c_{2}} \\ {\color{green}c_{3}} \end{pmatrix} + s\begin{pmatrix} {\color{brown}d_{1}} - {\color{green}c_{1}} \\ {\color{brown}d_{2}} - {\color{green}c_{2}} \\ {\color{brown}d_{3}} - {\color{green}c_{3}} \end{pmatrix} \end{eqnarray*}$

with $t\in\Re$ and $s\in\Re$ . Notice that if $s=0$ then we get the starting point of line $\overline{AB}$ and if $s=1$ then we get the ending point of line $\overline{AB}$ . Symmetrically, the same applies to $t=0$ , giving the start point of segment $\overline{CD}$ and $t=1$ , giving the end point of segment $\overline{CD}$ .

Equating the two equations for lines $\overline{AB}$ and $\overline{CD}$ , we obtain the system of linear equations:

$\begin{eqnarray*} {\color{cyan}a_{1}} + t({\color{blue}b_{1}}-{\color{cyan}a_{1}}) &=& {\color{green}c_{1}} + s({\color{brown}d_{1}}-{\color{green}c_{1}}) \\ {\color{cyan}a_{2}} + t({\color{blue}b_{2}}-{\color{cyan}a_{2}}) &=& {\color{green}c_{2}} + s({\color{brown}d_{2}}-{\color{green}c_{2}}) \\ {\color{cyan}a_{3}} + t({\color{blue}b_{3}}-{\color{cyan}a_{3}}) &=& {\color{green}c_{3}} + s({\color{brown}d_{3}}-{\color{green}c_{3}}) \\ \end{eqnarray*}$

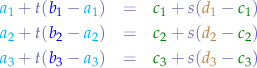
We determine $s$ and $t$ from the first two equations:

$\begin{eqnarray*} t &=& \frac{({\color{brown}d_{1}}-{\color{green}c_{1}})({\color{brown}d_{2}}-{\color{green}c_{2}})-({\color{brown}d_{2}}-{\color{green}c_{2}})({\color{cyan}a_{1}}-{\color{green}c_{1}})}{({\color{brown}d_{2}}-{\color{green}c_{2}})({\color{blue}b_{1}}-{\color{cyan}a_{1}})-({\color{brown}d_{1}}-{\color{green}c_{1}})({\color{blue}b_{2}}-{\color{cyan}a_{2}})} \\ s &=& \frac{({\color{blue}b_{1}}-{\color{cyan}a_{1}})({\color{cyan}a_{2}}-{\color{green}c_{2}})-({\color{blue}b_{2}}-{\color{cyan}a_{2}})({\color{cyan}a_{1}}-{\color{green}c_{1}})}{({\color{brown}d_{2}}-{\color{green}c_{2}})({\color{blue}b_{1}}-{\color{cyan}a_{1}})-({\color{brown}d_{1}}-{\color{green}c_{1}})({\color{blue}b_{2}}-{\color{cyan}a_{2}})} \end{eqnarray*}$

Note that the denominator, call it $\delta$ :

$\begin{eqnarray*} \delta &=& ({\color{brown}d_{2}}-{\color{green}c_{2}})({\color{blue}b_{1}}-{\color{cyan}a_{1}})-({\color{brown}d_{1}}-{\color{green}c_{1}})({\color{blue}b_{2}}-{\color{cyan}a_{2}}) \end{eqnarray*}$

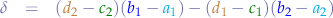
is the same for both $t$ and $s$ .

Judging on cases, we can say that:

if $\delta=0$ then the segments do not intersect,
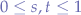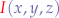if $0\le s, t \le1$ and the third equation is satisfied by $t$ and $s$ , then the lines intersect at the point ${\color{red}I}(x, y, z)$ , with the coordinates:

$\begin{eqnarray*} x &=& {\color{cyan}a_{1}} + s({\color{cyan}a_{2}} - {\color{cyan}a_{1}}) \\ y &=& {\color{blue}b_{1}} + s({\color{blue}b_{2}} - {\color{blue}b_{1}}) \\ z &=& {\color{green}c_{1}} + s({\color{green}c_{2}} - {\color{green}c_{1}}) \end{eqnarray*}$

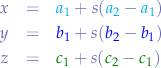
Implementation

The vectors A, B, C and D are given in parametric form, for example:

vector A = <34.517483, 231.703461, 21.108919>;
vector B = <34.517483, 222.014297, 21.108919>; 
vector C = <29.423143, 226.800842, 21.108919>;
vector D = <38.186848, 226.800842, 21.108919>;

In order to determine whether the segments $\overline{AB}$ and $\overline{CD}$ intersect, one would call the function as:

if(wasSegmentIntersect(A, B, C, D) == TRUE) {
    llOwnerSay("Segments AB and CD intersect.");
    return;
}
llOwnerSay("Segments AB and CD do not intersect.");

wasSegmentIntersect is defined as:

///////////////////////////////////////////////////////////////////////////
//    Copyright (C) 2014 Wizardry and Steamworks - License: GNU GPLv3    //
///////////////////////////////////////////////////////////////////////////
// determines whether the segment AB intersects the segment CD
integer wasSegmentIntersect(vector A, vector B, vector C, vector D) {
    vector s1 = <B.x - A.x, B.y - A.y, B.z - A.z>;
    vector s2 = <D.x - C.x, D.y - C.y, D.y - C.z>;
 
    float d = (s1.x * s2.y -s2.x * s1.y);
 
    if(d == 0) return FALSE;
 
    float s = (s1.x * (A.y - C.y) - s1.y * (A.x - C.x)) / d;
    float t = (s2.x * (A.y - C.y) - s2.y * (A.x - C.x)) / d;
 
    // intersection at <A.x + (t * s1.x), A.y + (t * s1.y), A.z + (t * s1.z)>;
    return (integer)(s >= 0 && s <= 1 && t >= 0 && t <= 1 && 
            A.z + t*(B.z - A.z) == C.z + s*(D.z - C.z));
}