Table of Contents
Overview
Properties
- The radius of the sphere circumscribing the icosahedron, spanning from the centre of the icosahedron to each vertex, is:

- The radius of the inscribed sphere, spamming from the centre of the icosahedron to each face, is:
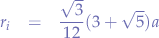
- The midradius that spans from the centre of the icosahedron to the middle of each edge, is:
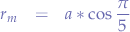
- The dihedral angle (the angle between the sides of any two triangles on the icosahedron) of the icosahedron is:

Inner Angle between Faces
We want to determine  which is the inner angle between two segments that connect the centre of the icosahedron to the centre of two adjacent triangles.
which is the inner angle between two segments that connect the centre of the icosahedron to the centre of two adjacent triangles.
In order to do that, we observe the kite formed by the points  :
:
In the yellow triangle, we observe that the segment 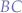 is the line from the side of triangle to the centroid and is equal to
is the line from the side of triangle to the centroid and is equal to  where, for an equilateral triangle,
where, for an equilateral triangle,  . We thus know that:
. We thus know that:
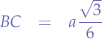
We also observe that  is the line from the centre of the icosahedron to the centroid of the triangle, which is equal to the radius of the inscribed sphere
is the line from the centre of the icosahedron to the centroid of the triangle, which is equal to the radius of the inscribed sphere 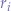 :
:
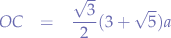
Now, for the triangle  we apply
we apply  :
:

and extract  :
:
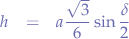
For triangle  , we apply
, we apply  and substitute
and substitute  :
:

To find out the numeric value, we substitute  and obtain
and obtain  :
:
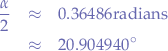
Thus,  is:
is:

For the contact, copyright, license, warranty and privacy terms for the usage of this website please see the contact, license, privacy, copyright.



