Equation of a Plane
Given a normal vector to the plane  , and
, and  ,
,  the position vectors of two points in the plane, then we have the vector form equation of a plane:
the position vectors of two points in the plane, then we have the vector form equation of a plane:
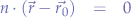
This can be expanded using commutativity:

in order to obtain:

Since each vector in the plane most be orthogonal to the normal vector  , then it means that the vector
, then it means that the vector  is a vector in the plane.
is a vector in the plane.
With some simplification and substituting 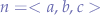 ,
,  and
and 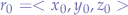 we obtain a parametric equation:
we obtain a parametric equation:
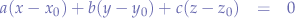
Find the Equation of a Plane Defined by Three Points
Since a plane is defined by three points in geometry, we can use the parametric equation form to determine the equation of the plane that contains all three points - there is only one such plane but can be described by several equations.
Suppose that the given points are:

We compute the normal vector by computing the cross-product of the vectors between any two points - for example, the vector  from
from  to
to  and the vector
and the vector  from
from  to
to  :
:

leadning to:
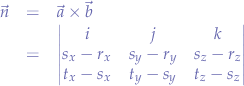
and expanding the determinant by the cofactors of  ,
,  and
and  :
:
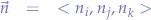
where:
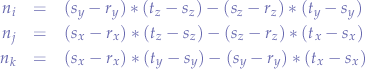
Next, in addition to the normal vector, we need a point to describe the plane by and we can pick any of the three points chosen. Any of the resulting equation will be valid. Let's pick the first one  which will lead to the plane equation:
which will lead to the plane equation:
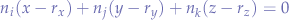
conversely, if we picked point  , we would have obtained:
, we would have obtained:
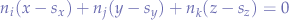
and, for point  :
:
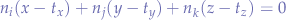
Any of these three equations describe a plane that contains all of the points  ,
,  ,
,  .
.
We can transform the equations back into vector form by knowing the normal vector  and making pairs of
and making pairs of  ,
,  and
and  :
:
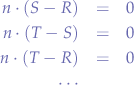
For the contact, copyright, license, warranty and privacy terms for the usage of this website please see the contact, license, privacy, copyright.



