Table of Contents
The Derivate
The derivate of a function 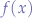 with respect to its variable
with respect to its variable  is the instantaneous rate of change (slope) of the function at any value of
is the instantaneous rate of change (slope) of the function at any value of  .
.
![LaTeX
\begin{tikzpicture}[domain=0:4]
% grid
\draw[help lines] (0,0) grid (4,4);
% origin
\draw[red, line width=.1mm] (-0.1,-0.1) -- (0.1,0.1)
(0.1,-0.1) -- (-0.1,0.1);
\coordinate[label={[red]below:$O$}] (O) at (0,0);
\draw[dotted,->] (O) -- (4,0) node[below] {$x$};
\draw[dotted,->] (O) -- (0,4) node[left] {$y$};
\draw[color=blue] plot[id=exp] function{0.05*exp(x)} node[right] {$y = f(x) = \frac{1}{20} \mathrm e^x$};
\coordinate[label={[red]below:$f(x_{1})$}] (F1) at (2, {1/20*exp(2)});
\drawpoint{F1}{.5mm}[red];
\coordinate[label={[red]above:$f(x_{2})$}] (F2) at (3.5, {1/20*exp(3.5)});
\drawpoint{F2}{.5mm}[red];
\draw[green] (F1) -- (3.5,{1/20*exp(2)}) node [below left] {$\Delta x$} -- (F2) node [below right] {$\Delta f$};
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/img9a61f77e5e1654b1b39106728f9c43fb.png)

Derivates of Common Functions
 is a constant, while
is a constant, while  ,
,  ,
,  are functions. The derivates are expressed as derivatives with respect to an arbitrary variable x.
are functions. The derivates are expressed as derivatives with respect to an arbitrary variable x.
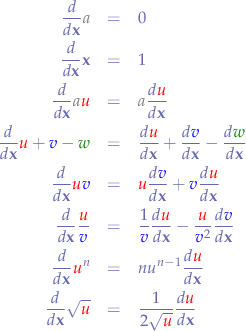
![Equations \begin{eqnarray*}
\frac{d}{d{\bf{x}}}\frac{1}{{\color{red}u}} &=& -\frac{1}{{\color{red}u}^2}\frac{d{\color{red}u}}{d{\bf{x}}} & \\
\frac{d}{d{\bf{x}}}\frac{1}{{\color{red}u}^{n}} &=& -\frac{n}{{\color{red}u}^{n+1}}\frac{d{\color{red}u}}{d{\bf{x}}} & \\
\frac{d}{d{\bf{x}}}[f({\color{red}u})] &=& \frac{d}{d{\color{red}u}}[f({\color{red}u})]\frac{d{\color{red}u}}{d{\bf{x}}} & \\
\frac{d}{d{\bf{x}}}[\ln{{\color{red}u}}] &=& \frac{d}{d{\bf{x}}}[\log_{e}{{\color{red}u}}]=\frac{1}{{\color{red}u}}\frac{d{\color{red}u}}{d{\bf{x}}} & \\
\frac{d}{d{\bf{x}}}[\log_{{\color{gray}a}}{\color{red}u}] &=& \log_{{\color{gray}a}}{e}\frac{1}{{\color{red}u}}\frac{d{\color{red}u}}{d{\bf{x}}} & \\
\frac{d}{d{\bf{x}}}e^{{\color{red}u}} &=& e^{{\color{red}u}}\frac{d{\color{red}u}}{d{\bf{x}}} & \\
\frac{d}{d{\bf{x}}}{\color{gray}a}^{{\color{red}u}} &=& {\color{gray}a}^{{\color{red}u}}\ln{{\color{gray}a}}\frac{d{\color{red}u}}{d{\bf{x}}} & \\
\frac{d}{d{\bf{x}}}{\color{red}u}^{{\color{blue}v}} &=& {\color{blue}v}{\color{red}u}^{{\color{blue}v}-1}\frac{d{\color{red}u}}{d{\bf{x}}}+{\color{red}u}^{{\color{blue}v}}\ln{{\color{red}u}}\frac{d{\color{blue}v}}{d{\bf{x}}} & \\
\end{eqnarray*}](/lib/exe/fetch.php?media=wiki:latex:/imgcc3ac47e722cdc789e4c460efb6602e2.png)
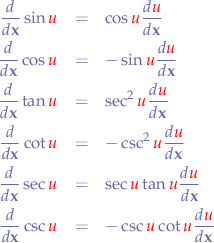
Partial Derivates
When there is more than one variable in a function it is often useful to examine the variation of the function with respect to one of the variables with all the other variables considered to stay constant.
Suppose we have a function:

then, the partial derivate with respect to  is written as:
is written as:
![LaTeX
\begin{eqnarray*}
\frac{\partial{F(x,y)}}{\partial{x}} &=& \frac{\partial}{\partial{x}}[ax^2+by^2] = 2ax
\end{eqnarray*}](/lib/exe/fetch.php?media=wiki:latex:/imgcb0d6603b0666864d7ec907c583de18d.png)
respectively, after deriving by  :
:
![LaTeX
\begin{eqnarray*}
\frac{\partial{F(x,y)}}{\partial{y}} &=& \frac{\partial}{\partial{y}}[ax^2+by^2] = 2by
\end{eqnarray*}](/lib/exe/fetch.php?media=wiki:latex:/img8ca1752a76d5aa7bae0b90650ead49cd.png)
Practical Applications
In physics, partial derivates are used to express various equations that rely on time. For example, the velocity  is the derivate of the position with respect to time:
is the derivate of the position with respect to time:
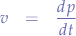
and acceleration is the derivative of velocity with respect to time (and hence the double derivate):
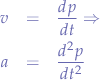
Combination of Functions
When applied to combination of functions certain properties of derivates apply.
Product of Two Functions
If a function 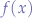 is a product of two functions
is a product of two functions 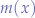 and
and 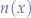 , then the derivate of this product is:
, then the derivate of this product is:

Sum of Two Functions
If the function 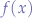 is a sum of two functions
is a sum of two functions 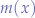 and
and 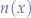 , then the derivate of this sum is:
, then the derivate of this sum is:
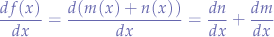
Chain Rule
If the function 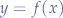 and
and 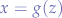 , then the derivative of
, then the derivative of  with respect to
with respect to  can be written as a product of derivates:
can be written as a product of derivates:
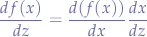
For the contact, copyright, license, warranty and privacy terms for the usage of this website please see the contact, license, privacy, copyright.



