Sleep Sort
Algorithm
- Spawn as many threads as there are elements in the list to sort.
- Make each thread sleep for the number of seconds corresponding to the number to sort.
- Receive the numbers in order as each thread recovers from sleep.
Performance
- Worst case:
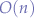
- Best case:
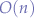
- Average case:
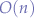
- Space complexity:
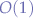
- Time taken:
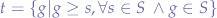 where
where  is the list to sort.
is the list to sort.
Remarks
- This is an
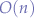 algorithm but it will effectively take as much time to sort a list of numbers as the value of the largest number in the list.
algorithm but it will effectively take as much time to sort a list of numbers as the value of the largest number in the list. - The numbers can be divided by some large constant to decrease the waiting time and the same constant can then be multiplied with the received numbers to get their original value.
- The algorithm relies on the fact that, time is linear and events will finish in order, regardless of computer performance.
- Be aware that spawning threads is not an atomic operation and that for sufficiently small numbers to sort, the actual spawning of the threads may interfere with the thread sleep time and break the algorithm.
Implementations
Notes
A [WaS] original - at least it consumes less CPU cycles than shaker short.
fuss/algorithms/sorting/sleep_sort.txt · Last modified: by 127.0.0.1
For the contact, copyright, license, warranty and privacy terms for the usage of this website please see the contact, license, privacy, copyright.




