Dijkstra's Shortest Path Algorithm

Algorithm

Note the distances from a current (initial) node to all neighbouring nodes.
Mark the current node as visited and move to the next node with the smallest distance and set it as the current node.
If the destination node is marked visited, stop.
Otherwise repeat at 1.

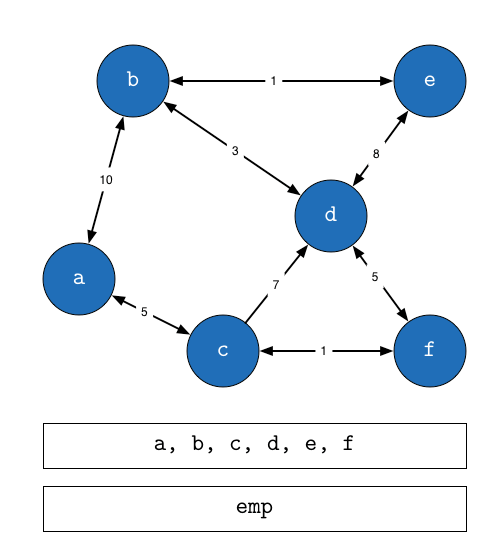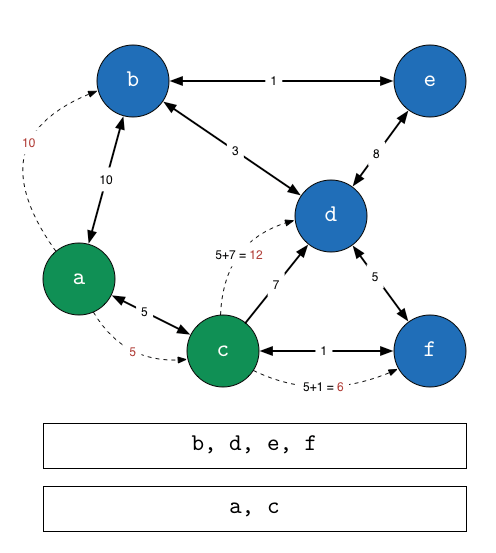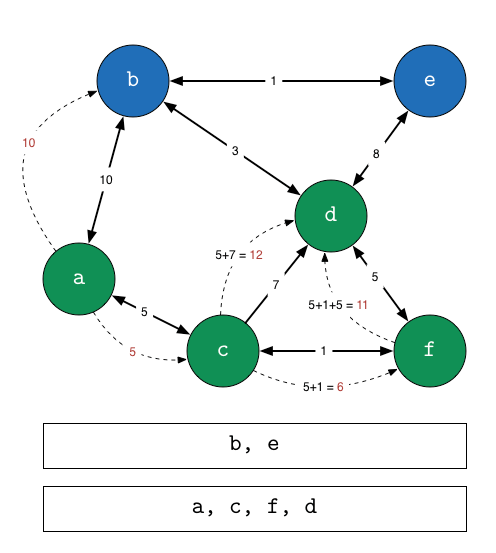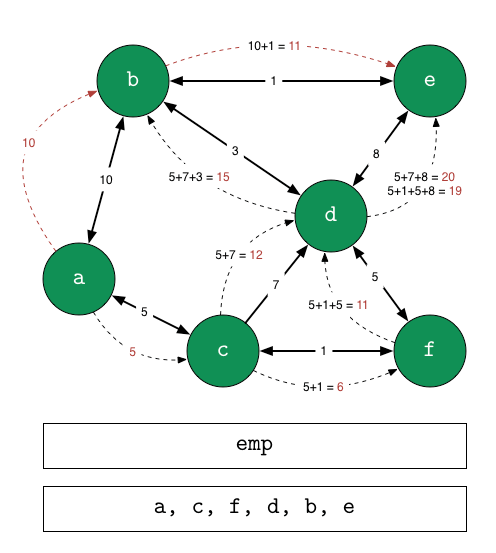
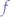Dijkstra's shortest path algorithm can be used for full traversal (illustrated in the animation) where all the nodes are visited in order to determine all the distances between node $a$ and node $e$ . However, one can observe in the illustration that when nodes $a$ , $b$ and $f$ are visited, the choice is given between following a path with weight $10$ to $b$ , a path of weight $12$ to $d$ and a path of weight $11$ to $d$ . In the illustration we chose a full traversal, that is, we visit $d$ , even though we could have directly selected the shortest path with weight $10$ from $a$ to $b$ .
One invariant for the full-traversal variant of Dijkstra is that there is a minimal path from a starting node to a destination node if and only if the queue of unvisited nodes is empty at the end.

Worst case: $O(|E| + |V|log|V|)$ where $|E|$ is the number of edges and $|V|$ is the number of vertices.