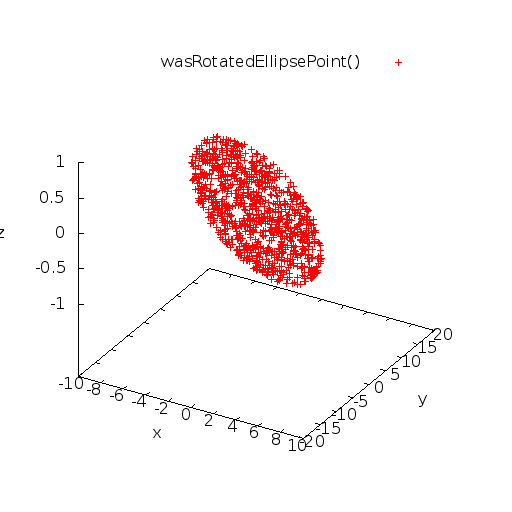
Graph

Theory

The code performs the follows the reasoning: for a chosen $a$ and $b$ , select a random $x$ with $x \in [0, a)$ and $y$ with $y \in [0, b)$ . If and only if the equation of the ellipse in standard form:

$\begin{eqnarray*} (\frac{x}{a})^{2}+(\frac{y}{b})^{2} &\le& 1 \end{eqnarray*}$

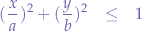
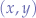is satisfied, then the generated $x$ and $y$ values describe a point $(x, y)$ which lies within the ellipse's perimeter. Otherwise, select new values for $x$ and $y$ and loop until the equation is satisfied.

Once a point within that ellipse is generated, we rotate the point on an arc described by the specified angle $\alpha$ (in radians):

$\begin{eqnarray*} x &\mapsto& x*\cos{\alpha} + y\sin{\alpha} \\ y &\mapsto& x*\sin{\alpha} - y\cos{\alpha} \end{eqnarray*}$

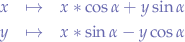
in order to obtain the rotated point.

Code

wasRotatedEllipsePoint.lsl

///////////////////////////////////////////////////////////////////////////
//    Copyright (C) 2015 Wizardry and Steamworks - License: GNU GPLv3    //
///////////////////////////////////////////////////////////////////////////
// the angle (in radians) o represents a rotation in the trigonometric 
// sense around the Ox axis where O represents the ellipse center
vector wasRotatedEllipsePoint(float a, float b, float o) {
    float x = llPow(-1, 1 + (integer) llFrand(2)) * llFrand(a);
    float y = llPow(-1, 1 + (integer) llFrand(2)) * llFrand(b);
    if(llPow(x/a,2) + llPow(y/b,2) <= 1)
        return <x*llCos(o) + y*llSin(o), x*llSin(o) - y*llCos(o), 0>;
    return wasRotatedEllipsePoint(a, b, o);
}

Table of Contents

Graph

Theory

Code