Table of Contents

Created by the Wizardry and Steamworks group.

TODO

Overview

The channel range in Second Life can be seen as an abstraction over a frequency spectrum, where each channel represents an individual unitary (positive or negative) frequency where channel 0 is reserved for public chatter.

In practice, the problem is that, even if the the range is abundantly high there is still a high probability that two scripts in an object or worn by an avatar will collide. For avatars, this may happen, for example, if both of them own the same product from the same creator. It may also happen, for example, since it is humanely easier for a script-writer to use, remember and re-use particular channel range (for example, $[1-10]$) rather than choosing a range between some arbitrary $x$ in the range $[-x, -x]$.

Other times, it is necessary to explicitly select a colliding channel: for example, the standard colliding channel chosen by RLV Traps via their own specification. Furthermore, any channel shared with other scripts, may considered a colliding channel even if the collisions are intentional (for example, the same object communicating with other parts of itself using channels - unlikely given llMessageLinked, yet still possible).

The main problem with colliding channels is that interference costs processing time. That is, whenever a script A receives a message, it will have to first check whether that message belongs to some other script B, not related (or not intended) for itself (A).

Suppose you have two scripts, named A and B, in the same region that communicate via a certain channel 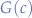$G(c)$: 

 +---+  G(c)  +---+
 | A |--------| B |
 +---+        +---+

Now, suppose there are two more scripts, named C and D that communicate via the same channel 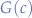$G(c)$: 

          +---+
 +---+    | B |
 | C |    +---+
 +---+   /
      \ /
       \ G(c)
      / \
 +---+   \
 | A |    \
 +---+     \
            +---+
            | D |
            +---+

This would make the channel 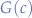$G(c)$, a colliding channel. However, Second Life still allows that, because the script pair 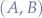$(A,B)$ may communicate by filtering out the interference caused by the communication of the script pair 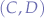$(C,D)$ which is done in the listen event in each script.

Channel Grate

We define the channel grate $G$ in Second Life as being a set defined by the full range of channels $[-214748364, 2147483647]$ that a script within objects may communicate on: 

G : [-214748364, 2147483647]

Intuitively, contrasting with real frequencies, the channel grate G in the context of Second Life represents the full spectrum of frequencies (all possible channels that two scripts may communicate on).

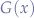A script may take a value $x$ from $G$, and the channel $G(x)$ will fall within the range $[-214748364, 2147483647]$ which is a subset of the integer set ℤ. 

G(x) : ℤ -> [-214748364, 2147483647]

It is interesting to note that the fact that the grate in Second Life is a subset of the integer-set G ⊆ ℤ, which greatly increases the probability of a collision compared to real-life frequencies where a grate is a subset of Q \ ℤ- which permits sub-divisions of positive integers, in programming known as floats. For example, a real-life frequency may be something like $102.64$ or $84.128$, whereas in Second Life, it may consist only of integers, something like $-4$ or $8$.

We define a script-group a group consisting of any amount of finite scripts: 

(A1,..,An)

Therefore, for a pair of scripts 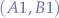$(A1,B1)$, communicating over a channel 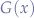$G(x)$, the overall probability of a collision is: 

Pc(G(x)) =  1/2362232011  = 4.23 * 10e-10

However, since the viewer policy states that avatars may only listen on the public channel 0, thereby forcing public interaction scripts to communicate over channel 0, the probability becomes much higher. Similarly, in the case of llDialog and llSetText queries, as explained in the first section, it is more common for a script-writer to use a range [1,100] than a range $[ -214748364, -214748264 ]$.

We can generalize over any number of scripts 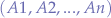$(A1,A2,...,An)$ communicating with any other number of scripts $(B1,B2,...,Bn)$: 

   +----+     +----+     +----+
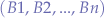   | A1 | ... | A2 | ... | An |
   +----+     +----+     +----+
     |          |          |
     |          +------+   |
     |G(y)              \ /
 ... + + + + + + + + + + + + ...   <--- Channel Grate
     |                 / |G(x)
     |          +-----+  +
     |          |         \
   +----+     +----+     +----+
   | B1 | ... | B2 | ... | Bn |
   +----+     +----+     +----+

as you can see, the 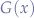$G(x)$ is a shared (colliding) channel and 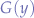$G(y)$ is a free (non-colliding) channel.

We define:

Also, based on the explanation, we informally define interference as being the chatter received on a script-group's channels sent by other scripts which was either not meant for that script-group or useless to that script-group.

The Problem

One of the problems is that the listening script, in the script-pair $(A1,B1)$ may contain something like: 

integer channel = 5;
default
{
  state_entry() {
    llListen(channel, "", "", "");
  }
  listen(integer channel, string name, key id, string message) {
    /* Assume the other script posts data here. */
  }
}

which would not apply for the script-group $(A2,...,An,B2,...,Bn)$ since any of the scripts in that script-group cannot assume whether anybody else except themselves are posting data on the shared channel $G(x)$.

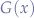In order to go around that problem, script-writers have to manually filter messages. Commonly, for a listener script in a script-group communicating on the (possibly) shared-channel 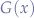$G(x)$, you could expect some derivate form of: 

integer channel = 5;
default
{
  state_entry() {
    llListen(channel, "", "", "");
  }
  listen(integer channel, string name, key id, string message) {
    /* Cannot assume anything. Filter time! */
    list message = llParseString2List(message, ["|"], []);
    if(llList2String(message, 1) == "Picasso") {
      /* Aha! It's Picasso speaking! */
    }
  }
}

which would mean that the other script, posting data on channel 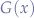$G(x)$ would send the message with an unique identifier "Picasso" in the first tokenized part of the data.

Conventionally, script-writers are taught to close the channels as soon as they are done with them and to avoid using the public channel 0 (at least by the llDialog LSL API specification's comments). The problem is that even if a message is not intended for a listening script, the listen event will be triggered within that script. In the example above, not only the listen event will be fired but also the listen event will use llParseString2List to convert it to a list, that list will have to be declared and then the first token of the string will have to be tested against "Picasso". That means that on a shared-channel 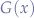$G(x)$ (in this case 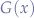$G(x)$ = 5), more events will be generated than necessary which will implicitly increase the resource usage of those scripts. There is no escape and the best that the script-writer may hope for is to at least guarantee, as can be seen from the script above, that the message received by the listening script will indeed be intended for that script provided that it passes all the tests in the listen event. However, the script-writer has no way of assuming that the received message will come from the intended script except by using the filters provided by llListen.

Even if the script-writer opens up the maximum number of channels in a script, the script will not cause any supplementary lag if there is no message received on those channels. listen will never be triggered in the first place, consequentially, following the example above, nor will the list be declared, converted to a string and then tested against "Picasso".

Furthermore, for in-world objects, the filters provided by llListen provide a very weak limitation when lots of data has to be exchanged, as it frequently is the case, and when the object might get de-rezzed at any point, thereby changing the key when it is rezzed in-world again. Let's look at the API specification for llListen: 

integer llListen( integer channel, string name, key id, string msg );

Sets a callback for msg on channel from name and id.
Returns an integer that can be used to deactivate or remove the listen.

• integer  channel   –   any valid integer (-2147483648 through 2147483647)
• string   name      –   filter for specific prim name or avatar legacy nam
• key      id        –   filter for specific prim/avatar UUID
• string   msg       –   filter for specific chat message

If msg, name or id are blank they are not used to filter incoming messages. If id is an invalid key or a null key, it is considered blank.

Usually, when speaking to avatars over channels, a filter based on a combination between channel and id is the most useful combination. When it comes to a primitive speaking to a primitive, a combination between channel and msg should suffice to at least filter out most of the interference. Even so, even if some interference fails to pass the tests in listen, the listen event will have been already triggered and possibly some operations would have been executed in order to check whether the message is useful and to filter out interference.

This provides very weak security at a very high cost of resources. Practically, for any listening in-world script, it is safe to assume that the possibility of at least a denial of service (DoS) is trivially possible, provided that you find out on what channel that script is listening on (which, we just informally add, is pretty easy to accomplish). The way that could be accomplished, would be to jam the channel with interference, homologous to how real-life frequency jamming works.

Jamming

Since we have mentioned Denial of Service, let us expand a bit more on this. Every operating system implements at kernel-level a scheduler which is used to allocate CPU time (mainly) to processes running on that system. The scheduler runs on what is called a scheduling policy which determines which process gets how much CPU time allocated. For example, in some cases where you have an institution that benefits from a cluster system which allows employees to perform computations using the whole clusters resources, the policy may be that only a group, a certain users or even a certain process itself will get a certain policy-enforced share of CPU time.

As a counter-example, on a default desktop oriented Linux system, the scheduler does not impose any certain policy and tries to satisfy all processes to the best of its abilities. That is, if a process requests more, it does all it can to give that process more. What happens in such a case, is that if you have several users accessing that system and one of them forks off some process that eats up the whole CPU, the other users will feel that the system is starting to gradually unstable and may even lock up completely (any resource-bombs as references to that example apply).

Now, let's take for example a SIM in Second Life with just one object, containing one script and let's call this script Bob. In this case, the whole CPU time is available to Bob.

Now, let's add another object with another script and let's call it Alice. Now, the whole CPU time will be divided equally between the two scripts on the SIM. At this point, it already becomes a push-and-pull game between Bob and Alice, and they are both racing the other to grasp more and more resources.

Also, let's suppose that both Bob and Alice have listen events and that Bob's listen event is not filtered at the level of llListen, but rather in the event handler itself, as described in the previous section.

Furthermore, assume that both Bob and Alice are trying to compute enough of $\pi$ to reach some integer after the decimal.

Now, let's suppose another script Eve is transferred into the SIM and starts to dish out nonce messages to Bob. She practically throws nonsense at Bob on Bob's channels with no particular meaning. Compared to Alice, Bob will have its listen event triggered and will have to start making sense of what Eve is trying to say. In this case, Bob will have to slow down the computation and offer some priority to the listen event that is constantly being fired.

The result, will of course be that Alice will win the computational challenge because Bob will be encumbered by having to make sense of meaningless messages munching its own allocated CPU time.

Example: Jamming

Meet Alice: 

integer run = 0;
 
float ITERATIONS = 1000.0;
 
string progress(integer percent, integer length, list symbols) {
    percent /= (integer)((float)100.0/(length));
    string p = llList2String(symbols,0);
    integer itra = 0;
    do {
        if(itra>percent-1) p += llList2String(symbols,2);
        else p += llList2String(symbols,1);
    } while(++itra<length);
    return p + llList2String(symbols,3);
}
 
float pie = 1;
 
default
{
    state_entry() {
        llSetText("Alice", <1,1,1>, 1);
        llListen(-50, "", "", "");
    }
    touch_start(integer num) {
        llSetObjectName("Alice");
        llSetTimerEvent(.01);
    }
    timer() {
        integer prog = (integer)llCeil(((float)run*100.0)/(ITERATIONS));
        llSetText("Alice:\n" + progress(prog, 10, ["[", "#", "o", "]"]) , <1,1,1>, 1);
        pie = 1 + run / (2.0 * run + 1) * pie;
        if(++run == ITERATIONS) {
            llSetTimerEvent(0);
            llOwnerSay((string)pie);
            llResetScript();
            return;
        }
        llSetTimerEvent(.01);
    }
    listen(integer channel, string name, key id, string message) {
        list tokens = llParseString2List(message, ["|"], []);
        if(llList2String(tokens, 0) == llGetObjectName()) {
            integer itra;
            for(itra=1; itra<llGetListLength(tokens); ++itra) {
                if(llList2String(tokens, itra) == "stop") {
                    llResetScript();
                }
            }
        }
    }
}

Meet Bob: 

integer run = 0;
 
float ITERATIONS = 1000.0;
 
string progress(integer percent, integer length, list symbols) {
    percent /= (integer)((float)100.0/(length));
    string p = llList2String(symbols,0);
    integer itra = 0;
    do {
        if(itra>percent-1) p += llList2String(symbols,2);
        else p += llList2String(symbols,1);
    } while(++itra<length);
    return p + llList2String(symbols,3);
}
 
float pie = 1;
 
default
{
    state_entry() {
        llSetText("Bob", <1,1,1>, 1);
        llListen(-100, "", "", "");
    }
    touch_start(integer num) {
        llSetObjectName("Bob");
        llSetTimerEvent(.01);
    }
    timer() {
        integer prog = (integer)llCeil(((float)run*100.0)/(ITERATIONS));
        llSetText("Bob:\n" + progress(prog, 10, ["[", "#", "o", "]"]) , <1,1,1>, 1);
        pie = 1 + run / (2.0 * run + 1) * pie;
        if(++run == ITERATIONS) {
            llSetTimerEvent(0);
            llOwnerSay((string)pie);
            llResetScript();
            return;
        }
        llSetTimerEvent(.01);
    }
    listen(integer channel, string name, key id, string message) {
        list tokens = llParseString2List(message, ["|"], []);
        if(llList2String(tokens, 0) == llGetObjectName()) {
            integer itra;
            for(itra=1; itra<llGetListLength(tokens); ++itra) {
                if(llList2String(tokens, itra) == "stop") {
                    llResetScript();
                }
            }
        }
    }
}

Bob and Alice will race each other to the pie. The pie is defined as: 

pie = 1 + run / (2.0 * run + 1) * pie;

vaguely as a reference to calculating PI recursively using Newton's method. However, in this case it does not apply and any computation made in the timer event will not influence the outcome of the experiment.

Now, meet Eve: 

string payload = "Bob";
 
default
{
    state_entry() {
        llSetText("Eve", <1,1,1>, 1);
    }
    touch_start(integer num) {
        state jam;
    }
}
 
state jam
{
    state_entry() {
        llSetTimerEvent(.001);
    }
    timer() {
        llSetText("Eve, jamming...\nPayload Size: " + (string)llStringLength(payload), <1,1,1>, 1);
        payload += "|" + "stoa";
        llSay(-100, payload);
    }
    touch_start(integer num) {
        llResetScript();
    }  
}

The video below shows Eve jamming Bob and then, in the second part, Eve jamming Alice (you may have to switch to 720p to see the text displayed above the primitives since the text is all that really matters):

Both Alice and Bob try to determine in their listen events whether they have received a "stop" token. However, when Eve jams either one of them, she never sends a full "stop" message but rather a long stream of tokens with "stoa" instead. This basically plays the llList2String comparison between "stop" and "stoa". Alternatively, one could have changed the very last letter "a" to any other letter of symbol every single round to avoid caching (if there would be such a thing).

Another component is that both Alice and Bob run through the full list of tokens, however that just makes it easier to illustrate. Even if we were to optimize the listen events for both Alice and Bob (perhaps using llListFindList) and even if Eve would not know to send "Alice" or "Bob" as the first token, there still would be some workload induced by Eve. Which is simply the result of the listen handler stepping in and processing the messages it hears on the channels installed by llListen.

In any case, this is a typical form of DoS with some man-in-the-middle flavors. However, of course, we can spawn as many Eves as we like and turn the DoS into a distributed DoS (DDoS) which would render this attack much more effective.

Later on, we will watch another video of Frequency Hopping Bobs and Alices illustrating how the jamming may be prevented using the techniques described in this article.

Interference

Regardless whether the script is under a DoS siege, or whether the interference is just conjecture of a different script-group communicating over a shared channel 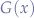$G(x)$, the work cycles increase proportionally to the amount of scripts pushing data on that channel.

We define:

For every active script, the interference I on channel x is given by: 

I(G(x)) = the total unique number of scripts posting data on channel G(x) - the number of validly communicating scripts

We assume that all scripts are active and let's reason inductively over our previous examples:

Base case: 

 +---+   c   +---+
 | A |-------| B |
 +---+       +---+

Two scripts and one shared bi-directional channel. There is no third-party interference and all messages may be assumed meaningful. 

the number of validly communicating scripts = 2
I(G(c)) = 2 - the number of validly communicating scripts = 0

Base case+1: 

          +---+
 +---+    | B |
 | C |    +---+
 +---+   /
      \ /
   G(c)+
      /
 +---+
 | A |
 +---+

A script-group (A,B) and a jammer script C. 

the number of validly communicating scripts = 2
I(G(c)) = 3 - the number of validly communicating scripts = 1

Base case+2: 

          +---+
 +---+    | B |
 | C |    +---+
 +---+   /
      \ /
       \ G(c)
      / \
 +---+   \
 | A |    \
 +---+     \
            +---+
            | D |
            +---+

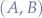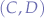Two script groups $(A,B)$ and $(C,D)$ communicating over the shared channel 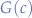$G(c)$. In this case, the interference is: 

the number of validly communicating scripts = 2
I(c) = 4 - the number of validly communicating scripts = 2

Base case+3: 

          +---+
 +---+    | B |
 | C |    +---+
 +---+   /
      \ /    +---+
   G(c)\-----| E |
      / \    +---+
 +---+   \
 | A |    \
 +---+     \
            +---+
            | D |
            +---+

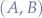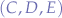Two script groups $(A,B)$ and $(C,D,E)$ communicating over shared channel 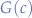$G(c)$. That gives us: 

the number of validly communicating scripts = 2
I(G(c)) = 5 - the number of validly communicating scripts  = 3.

Finally, base case + n: 

                    .
                    .
                    .
          +---+   +---+
 +---+    | B |   | E |
 | C |    +---+   +---+
 +---+   /       /
      \ /       / +---+
   G(c)\-------+--| F |
      / \       \ +---+
 +---+   \       \
 | A |    \       +---+
 +---+     \      | G |
            +---+ +---+
            | D |   .
            +---+   .

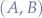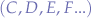Two script groups $(A,B)$ and $(C,D,E,F...)$ communicating over shared channel 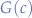$G(c)$. That gives us the total interference: 

I(G(c)) = n - the number of validly communicating scripts

where n is the total amount of unique scripts hitting a listen event. For example, the keys of all the scripts that trigger the interference calculating script (including its own key).

For example, suppose we have 3 total unique communicating scripts and 2 validly communicating scripts. In that case, 

I(G(c)) = 3-2 = 1

Which indicates that the channel 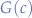$G(c)$ is being interfered with.

Based on those calculations, we can deduce ways to sense whether the communication between two scripts is being interfered with.

Sensing Interference

Thus, if we know the amount of legally participating scripts (and it is trivial to know that since we are writing the scripts anyways), we can assume that if the number of unique triggers of listen exceeds that value, then the channel is being jammed.

One observation, that might be made by reading the sub-sections of this particular section, is that these scripts still implement a filtering check, just like the original "problematic" script that used up resources did. However, while that would be an astute observation, it would also be imprecise because the article does not only describe sensing the interference, but also re-channeling. That is, while the "problematic" script would continue to process messages from a colliding channel, the re-channeling described in this article will make the script hop to a new channel and although it will still have to check for interference, it will only have to do that for a limited number of valid scripts meant to communicate with it.

The purpose of this article is to drastically reduce the processing cycles caused by potential interference to a minimum, not to eliminate all the efforts to determine if there is any interference.

Re-Channeling

How to re-channel is a question that forks into several other composite questions:

And a derivate thereof:

Choosing the next channel has and is an ongoing tantrum of many people. However, most people needing frequency hopping re-channeling algorithms, ask the question differently: how to choose the channel so that an adversary will not guess it? Or, even worse: how to choose the channel so that an adversary will not be able to programmatically determine it?

Let's reason about this the daft way. Suppose we are communicating on channel 69. Furthermore, suppose that an adversary figured out that we are communicating on channel 69. Now, suppose that our re-channeling function simply re-channels by incrementing the old channel by 1 (note that we have passed the old channel in both the hard way and the serene way in the scripts above): 

integer comHandle;
 
reChannel(integer channel) {
  ++channel;
  llListenRemove(comHandle);
  comHandle = llListen(channel, "", "", "");
}

Although we have re-channeled by incrementing the channel by 1, if the adversary knows that we were communicating on channel 69, it would be easy for the adversary to guess that the re-channeling is done by incrementing the value of the last used channel. Thus, the adversary will deduce that the next channel is 70 and start again and keep hopping along with us and interfere with us every single time. Not only that, but knowing that the amount of channels have an upper bound, eventually the script will try to llListen over those bounds. Thus, the adversary will use us as a sledge to send us hurling to a crash or disconnect (since the llListen LSL API does not state what happens if you try to llListen over the range, and since we have not bothered to check, nor will we do so right now, we shall not care - suppose gremlins happen).

The choice of the term "adversary" does not necessarily imply a person with a woolen hat holding a shovel, a knife and a flashlight. An adversary could be a script that uses the same algorithm to re-channel its own channels and may throw both script-groups into a re-channeling deadlock. Pretty much how you happen to sometimes run into somebody and then keep attempting to dodge them on the left, on the right and still keep bumping into them (until you empathically negotiate complementary trajectories - more on that later in this article).

Of course, the less-daft solution would be to use the LSL pseudo-random number generator: 

integer comHandle;
 
reChannel(integer channel) {
  channel = (integer) llFrand(-214748364);
  llListenRemove(comHandle);
  comHandle = llListen(channel, "", "", "");
}

However, to be complete, the people pondering the next-hop channel have ways (statistical analysis) to gather data and then determine the next channel-hop of an adversary. Thus, the re-channeling function is a matter of cryptography and therefore is usually classified. Since we would prefer drinking and partying than giving in to paranoia, let's suppose that llFrand has not yet been broken by somebody that figured out how pseudo the pseudo is in pseudo-random number generator. If you are still paranoid about that, you could simply add some stuff every time you reChannel(), therefore adding your own pseudo on top of the pseudo in pseudo-random number generator: 

integer comHandle;
 
reChannel(integer channel) {
  llListenRemove(comHandle);
  total_unique_triggers = [];
@recalculate;
  channel += (integer) llFrand(-214748364);
  if(channel == 0) jump recalculate; /* Avoid the public channel. If 0, recalculate the channel. */
  comHandle = llListen(channel, "", "", "");
}

And if we send the new channel through the old channel: 

integer comHandle;
 
reChannel(integer channel) {
  llListenRemove(comHandle);
  total_unique_triggers = [];
  integer oldChannel = channel;
@recalculate;
  channel += (integer) llFrand(-214748364);
  if(channel == 0) jump recalculate; /* Avoid the public channel. If 0, recalculate the channel. */
  llSay(oldChannel, "rechannel|" + (string)channel);
  comHandle = llListen(channel, "", "", "");
}

Concerning sending over the new channel, we could do it in many different ways. One would be to simply use the old channel (although the person with the woolen hat, if they already have have access to the old channel, may read out the re-channeling request and the new channel). One other way perhaps, may use llHTTPRequest to send it over but that would load the script a bit more than we want to.

Example: Re-Channeling on Interference

From the above, whenever 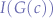$I(G(c))$ is greater than 0, we can assume that there is some interference and we re-channel. 

integer valid_scripts =  2; /* n  = 2 and represents the number of scripts that should communicate. */
list total_unique_triggers = []; /* Empty at first, will hold all the unique keys of other scripts interfering with this script. */
 
integer comHandle;
 
reChannel(integer channel) {
@recalculate;
  channel += (integer) llFrand(-214748364);
  if(channel == 0) jump recalculate; /* Avoid the public channel. If 0, recalculate the channel. */
  llListenRemove(comHandle);
  comHandle = llListen(channel, "", "", "");
}
 
default
{
  state_entry() {
    total_unique_triggers = [];
    comHandle = llListen(channel, "", "", "");
  }
  listen(integer channel, string name, key id, string message) {
        if(!~llListFindList(total_unique_triggers, (list)id)) { /* If this trigger of listen() by id is NOT in the list of total_unique_triggers ... */
            /* ... add it. */
            total_unique_triggers += id;
        }
        integer interference =  llGetListLength(total_unique_triggers)-valid_scripts; /* I(G(c))  = n - the number of validly communicating scripts. */
        if(interference > 0) { /*If we have any interference, then... */
            /* ... it is feasible to assume that we are being jammed. Re-Channel! */
            reChannel(channel);
            return;
        }
  }
}

Now Alice will get a new friend Allie with which she will exchange PING-PONG messages. Eve will try to interfere and jam Alice intending to slow her her down. However, this time Alice and Allie will re-channel together when they sense interference. The PING-PONG exchange will be re-established shortly thereafter and the relative distances between Alice and Bob will be preserved.

Bob will remain the same, however Alice will have to be pimped: 

integer valid_scripts =  2; /* LT(X)  = 2 and represents the number of scripts that should communicate. */
list total_unique_triggers = []; /* Empty at first, will hold all the unique keys of other scripts interfering with this script. */
 
integer comHandle;
 
reChannel(integer channel) {
  llListenRemove(comHandle);
  total_unique_triggers = [];
  integer oldChannel = channel;
@recalculate;
  channel += (integer) llFrand(-214748364);
  if(channel == 0) jump recalculate; /* Avoid the public channel. If 0, recalculate the channel. */
  llOwnerSay("Hopping to: " + (string)channel);
  llSay(oldChannel, "rechannel|" + (string)channel);
  comHandle = llListen(channel, "", "", "");
}
 
integer run = 0;
 
float ITERATIONS = 1000.0;
 
string progress(integer percent, integer length, list symbols) {
    percent /= (integer)((float)100.0/(length));
    string p = llList2String(symbols,0);
    integer itra = 0;
    do {
        if(itra>percent-1) p += llList2String(symbols,2);
        else p += llList2String(symbols,1);
    } while(++itra<length);
    return p + llList2String(symbols,3);
}
 
float pie = 1;
 
default
{
    state_entry() {
        total_unique_triggers += llGetKey();
        llSetText("Alice", <1,1,1>, 1);
        comHandle = llListen(-50, "", "", "");
    }
    touch_start(integer num) {
        llSetObjectName("Alice");
        llSetTimerEvent(.01);
    }
    timer() {
        integer prog = (integer)llCeil(((float)run*100.0)/(ITERATIONS));
        llSetText("Alice:\n" + progress(prog, 10, ["[", "#", "o", "]"]) , <1,1,1>, 1);
        pie = 1 + run / (2.0 * run + 1) * pie;
        if(++run == ITERATIONS) {
            llSetTimerEvent(0);
            llOwnerSay("Victory!");
            llResetScript();
            return;
        }
        llSetTimerEvent(.01);
    }
    listen(integer channel, string name, key id, string message) {
        if(!~llListFindList(total_unique_triggers, (list)id)) { /* If this trigger of listen() by id is NOT in the list of total_unique_triggers ... */
            /* ... add it. */
            total_unique_triggers += id;
        }
        integer interference =  llGetListLength(total_unique_triggers)-valid_scripts; /* I(G(c))  = n - 2 re-calculate the interference now. */
        if(interference > 0) { /* I(G(c)) > LT(X) the interference on this channel is higher than the amount of legal unique triggers.
            /* It is feasible to assume that we are being jammed. Re-Channel! */
            reChannel(channel);
            return;
        }
        list tokens = llParseString2List(message, ["|"], []);
        if(llList2String(tokens, 0) == llGetObjectName()) {
            if(llList2String(tokens, 1) == "PING") {
                llOwnerSay("PONG");
                llSay(channel, name+"|PONG");
                return;
            }
            integer itra;
            for(itra=1; itra<llGetListLength(tokens); ++itra) {
                if(llList2String(tokens, itra) == "stop") {
                    llResetScript();
                }
            }
        }
    }
}

And her new friend Allie is just sending her PING-PONG messages, while making sure that she also listens for re-channeling: 

integer comHandle;
 
default
{
    state_entry() {
        llSetText("Allie", <1,1,1>, 1);
        llSetTimerEvent(5);
        comHandle = llListen(-50, "", "", "");
    }
    touch_start(integer num) {
        llSay(-50, "Alice|PING");
    }
    listen(integer channel, string name, key id, string message) {
        list tokens = llParseString2List(message, ["|"], []);
        if(llList2String(tokens,0) == "rechannel") {
            llListenRemove(comHandle);
            integer newChannel = llList2Integer(tokens, 1);
            llOwnerSay("Hopping to: " + (string)newChannel);
            comHandle = llListen(newChannel, "", "", "");
            llSay(newChannel, "Alice|PING");
            return;
        }
        if(llList2String(tokens, 0) == llGetObjectName()) {
            if(llList2String(tokens, 1) == "PONG") {
                llOwnerSay("PING");
                llSay(channel, name+"|PING");
                return;
            }
        }
    }
}

Finally, we can see the video where Alice and Allie dodge the interference from Eve by re-channeling once Eve starts to jam Alice:

Of course, in all these cases, all the objects are named so it would be easy to set-up a filter, however nothing prevents another object, such as Eve to pose as Alice or Allie. Furthermore, all the cases in which it is impossible to set up a filter using llListen apply to this scenario as well.

Secure Re-Channeling

Let's play with protocols and see how a re-channeling session could be represented between two scripts: 

  .                      .
+---+  +----G(c)----+  +---+
| A |--+   -G(d)    +--| B |  A detects interference on channel G(c).
+---+      -G(e)       +---+
  .                      .
  .                      .
+---+  +----G(c)----+  +---+  A re-computes a new channel G(e), starts
| A |--+   -G(d)    |->| B |  listening on it and sends the new channel
+---+  +----G(e)       +---+  G(e) over the old channel G(c).
  .                      .
  .                      .
+---+      -G(c)       +---+  B then drops the old channel it was listening
| A |--+   -G(d)   +---| B |  on and starts listening on the new channel G(e)
+---+  +----G(e)---+   +---+  computed by the first script.
  .                      .

This could be considered the base-case where only one script re-channels and the other accepts. This may be problematic, supposing that Eve (the person with the woolen hat) may inject a re-channel request on channel 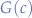$G(c)$ and knock B out because B will jump to some Eve-chosen channel, thereby breaking the communication forever with A. Not only that, but now Eve has divided A from B and may start conquering B by sending its own commands to it (nasty!). 

  .                      .
+---+  +----G(c)----+  +---+
| A |--+   -G(d)    +--| B |  A detects interference on channel G(c).
+---+      -G(e)       +---+
  .                      .
  .                      .
+---+  +----G(c)----+  +---+  A re-computes a new channel G(e), starts
| A |--+   -G(d)    |->| B |  listening on it and sends the new channel
+---+  +----G(e)       +---+  G(e) over the old channel G(c).
  .                      .
  .                      .
+---+      -G(c)       +---+  B then re-computes a new channel G(d),
| A |--+   -G(d)---+---| B |  starts listening on it and if A is chatting
+---+  +----G(e)---+   +---+  on that new channel G(e), then B sends the
  .                      .    new channel G(d) over A's new channel G(e).
  .                      .
+---+      -G(c)       +---+   The final channel both scripts will be
| A |-------G(d)-------| B |   listening on is G(d).
+---+      -G(e)       +---+
  .                      .

This is better because now, Eve will not be able to knock B out of the communication with A since B will check in the 3rd step to see if it is really talking to A over A's new channel 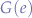$G(e)$ instead of Eve's forged channel.

However, that will not stop Eve sniffing the new channel sent by A, nor will it prevent Eve from sniffing the new channel sent by B in steps 2 and 3. That is where cryptography comes into play and if you want to be secure, then add an additional layer of encryption between A and B so that all the contents of the messages exchanged by A and B are scrambled from Eve's perspective. If you want to push the envelope, consider changing the cryptographic key as well whenever a re-channeling takes place.

Anonymity by Identity Castling

The concept of privacy and anonymity has been fascinating us for a while, and although you should go the llFrand way and be a good non-paranoiac because nobody will obsessively seek to sniff your curtain-control channels (except the curtain-obsessed people, of course) let us take a shot at this.

In Second Life every object is named and the name of the object is sent along with the message on channels which, would let Eve know A and B's identity.

Under the assumption that Eve does not know (and unable to find out) the true identity (object keys, similar to biological samples) of A and B, but knows that A and B are chatting, when can Eve assume that A is A and B is B?

To throw Eve off, we proceed by doing something called (named a minute ago, and pulled out of our Wizard's… sleeve) identity castling. It is what you may know from chess, where the Rook and the King exchange positions (a Rookade). We make the same move by exchanging the identity of A and B and finally changing both identities to something completely different when the new, final channel has been established. Again, remember that A's and B's biological samples (true identity, in the context of Second Life, the object keys) are unknown to Eve (she does not scan A or B for their keys). 

  .                      .
+---+  +----G(c)----+  +---+
| A |--+   -G(d)    +--| B |  A detects interference on channel G(c).
+---+      -G(e)       +---+
  .                      .
  .                      .
+---+  +----G(c)----+  +---+  A re-computes a new channel G(e), starts         Additionally A renames itself to B
| A |--+   -G(d)    |->| B |  listening on it and sends the new channel        after  sending the new channel G(e)
+---+  +----G(e)       +---+  G(e) over the old channel G(c).                  to B.
  .                      .
  .                      .
+---+      -G(c)       +---+  B then re-computes a new channel G(d),           Additionally, B renames itself to A
| B |--+   -G(d)---+---| A |  starts listening on it and if A is chatting      before sending the new channel G(d)
+---+  +----G(e)---+   +---+  on that new channel G(e), then B sends the g     to A.
  .                      .    new channel G(d) over A's new channel G(e).
  .                      .
+---+      -G(c)       +---+  The final channel both scripts will be
| B |-------G(d)-------| A |  listening on is G(d).
+---+      -G(e)       +---+
  .                      .
  .                      .
+---+      -G(c)       +---+                                                   When the connection is established,
| C |-------G(d)-------| D |                                                   the two objects rename themselves to
+---+      -G(e)       +---+                                                   something else.
  .                      .

Since Eve has no other information with regards to where the messages are coming from, other than the name of the object (for example, Eve is in the same region as A and B and A and B are exchanging messages via llRegionSay), Eve will see the following sequence, mapped precisely to the steps depicted above: 

A->B
A->B
A->B
A->B
... huh?

Again, since there is no information where A or B is positioned, A→B and B←A are equivalent.

That is, during the whole re-channeling negotiation, Eve will see A talking to B. If the exchange is additionally encrypted, Eve will at most know that A and B are re-channeling by monitoring the entire grate G. However, when the new channel is established and supposing Eve does not have the computational power to break the cryptographic key of the messages containing the re-channeling sequence as fast as A and B are exchanging them, then the new channel is unknown to Eve and when both objects change their names to something else, Eve is left completely clueless where A and B disappeared. The most Eve may assume at the end is that A and B re-channeled and vanished (to some far far away island where they will have lots and lots of… communication… privately and anonymously).

Given other objects in the region communicating over the grate, Eve cannot pragmatically make the link between the former A and B scripts. This can, for example, be a form of plausible deniability for A and B since Eve has cannot infer, given other scripts in the region communicating over the grate, that C is the former script A and D is the former script B.

Poincaré–Einstein Synchronization and Side-Channel Attacks

If we may be so bold, the Poincaré–Einstein synchronization is a method developed by Albert Einstein in order to synchronize remote clocks by the means of exchanging signals. The idea stems from the observation that boats docked at bay tend to flock together after a given amount of time. The same pattern applies to flotsam (yes, it is not just pure coincidence that Robinson Crusoe always gets drifted off to some beautiful island) and we would wager to thing that it applies to any system that exchanges messages - in reality, everything exchanges signals, be they voice, impulses or otherwise.

The experiments we wrote up, lead us further towards the Poincaré–Einstein synchronization and we hypothesized that given two primitives that exchange messages and having two separated, even isolated clocks on the same thread, will eventually lead to those clocks being synchronized. If the same effect happens in real-life, the same will have to apply to Second Life as well since the Poincaré–Einstein synchronization applies on a very subtle level of abstraction that no networked system will be able to escape.

Thus, to prove our theories, on an experimental level, 18 days ago we created two primitives with two simple and symmetric script. One of them called Tick and the other one called Tack.

Tick: 

integer _simTime=0;
 
default
{
    state_entry() {
        llSetColor(<1,1,1>, ALL_SIDES);
        llSetTimerEvent(1);
        llListen(9347572, "Tack", "", "PONG");
    }
    touch_start(integer num) {
        if(llDetectedKey(0) != llGetOwner()) return;
        llWhisper(9347573, "PING");
    }
    listen(integer channel, string name, key id, string message) {
        llSetColor(<1,0,0>, ALL_SIDES);
        llWhisper(9347573, "PING");
    }
    timer() {
        ++_simTime;
        llSetText((string)(_simTime/3600) + ":" + (string)((_simTime % 3600) / 60) + ":" + (string)((_simTime % 3600) % 60), <1,1,1>, 1);
 
    }
}

and Tack: 

integer _simTime=0;
 
default
{
    state_entry() {
        llSetColor(<1,1,1>, ALL_SIDES);
        llSetTimerEvent(1);
        llListen(9347573, "Tick", "", "PING");
    }
    touch_start(integer num) {
        if(llDetectedKey(0) != llGetOwner()) return;
        llWhisper(9347572, "PONG");
    }
    listen(integer channel, string name, key id, string message) {
        llSetColor(<1,0,0>, ALL_SIDES);
        llWhisper(9347572, "PONG");
    }
    timer() {
        ++_simTime;
        llSetText((string)(_simTime/3600) + ":" + (string)((_simTime % 3600) / 60) + ":" + (string)((_simTime % 3600) % 60), <1,1,1>, 1);
 
    }
}

We saved the scripts and then touched one of the primitives (in the Figure 1,2. below, the first started counter is the one on the upper left, relative to the camera). Then we waited 4 seconds and then touched the other primitive. This displayed a relative time-delta of 4 seconds between the two time-counters between the two primitives.

No change was visible for a long while and thanks to the University of New Orleans sandbox, we managed to leave the scripts running for a while.

Figure 1. No delta visible, perhaps half a second or so.

After 18 days, the results may be observed in Figure 1,2.

Figure 2. A fast snapshot when the clocks are perfectly identical.

How Can This Happen?

Looking at the code we used, the two scripts set-up a timer event every second which displays the overhead counter, expressed in hours, minutes and seconds. When either of the primitives is touched, it starts exchanging messages with the other primitive. For canonicity's sake, Tick sends a PONG string to Tack over channel 9347573 and Tack answers back with a PONG message to Tick over channel 9347572.

Since a primitive cannot listen] to itself, it would have been moderately safe to use the same channel. However, we did not want to risk that because, in case the channel would be shared (ie: a primitive may trigger its own listen event handler), then we speculate that the time delta will not diminish and that no synchronization would be possible.

In some ways, the system we have set-up contrasts nicely with a very fast recursive procedure where no event frequency limitations are imposed: in other words, Tick and Tack trigger each-other chaotically without any limitation except the upper limitations imposed by Linden.

We believe the outcome is explainable based on the previous article: every single message sent from either primitives will induce a small, almost insignificant computational delay in the other primitive. In general terms, and repeating the above: every single little function call and even a simple assignment instruction induces a little delay in the other script. That is, every single time one of the primitives receive a message, the timer event being susceptible to lag, like everything else, suffers a minor (perhaps microsecond) computationally induced lag. Since the two primitives are exchanging messages, it becomes a push and pull game between the two primitives: they each delay the other by throwing and catching messages using llWhisper to send and the listen event to catch. After some time, the two powers even out and the two primitives Tick and Tack become synchronized to some common value.

This can be proved by appealing to the physics model of dampened harmonic oscillators (after all, pendulums are another good example of Einstein's synchronization). One primitive pulls the other primitive. Then, the other primitive pulls the first primitive. This tug-of-war ends-up in a neutral state where the forces cancel each-other out.

The message itself represents a signal:

…

Thanks