Deriving Heron's Formula for the Area of a Triangle
![LaTeX
\begin{tikzpicture}
% grid
\draw[help lines] (-3,-3) grid (5,3);
% coordinates
\coordinate[label={[black]right:$B$}] (B) at (1.5,2.5);
\coordinate[label={[black]left:$C$}] (C) at (-2.5,-2);
\coordinate[label={[black]right:$A$}] (A) at (3,-2);
% height projection
\coordinate[label={[black]south east:$D$}] (D) at (1.5,-2);
\drawpoint{D}{.5mm}{black}
% side labels
\coordinate[label={[violet]south east:$a$}] (a) at (-0.75,0.75);
\coordinate[label={[green]south east:$c$}] (c) at (2.5,0);
\coordinate[label={[red]south east:$h$}] (h) at (1,0);
% triangle
%\draw[black, line width=.1mm] (A) -- (B) -- (C) -- cycle;
\draw[green, line width=.1mm] (A) -- (B);
\draw[violet, line width=.1mm] (B) -- (C);
\draw[blue, line width=.1mm] (A) -- (C);
% perpendicular
\draw[dashed, red, line width=.1mm] (B) -- (D);
% braces
%\drawbrace{B}{C}{6mm}{blue}{$a$}{0}{-8mm}{mirror}
%\drawbrace{A}{B}{6mm}{green}{$c$}{-6mm}{6mm}{mirror}
%\drawbrace{A}{C}{6mm}{cyan}{$b$}{8mm}{4mm}{}
%\drawbrace{A}{D}{2mm}{red}{$h$}{-4mm}{0mm}{mirror}
\drawbrace{D}{A}{2mm}{black}{$x$}{0mm}{-4mm}{mirror}
\drawbrace{C}{D}{2mm}{black}{${\color{blue}b}-x$}{0mm}{-4mm}{mirror}
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/imgcd1f91de281c1f9a09393886599eb9e4.png)
Let:
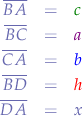
thus:
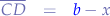
We apply Pythagoras in the triangle  in order to extract
in order to extract  :
:
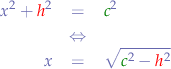
in order to obtain one equation.
We apply Pythagoras in the triangle  and obtain:
and obtain:
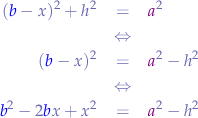
in order to obtain another equation.
Then we substitute  from the first equation into the second and obtain:
from the first equation into the second and obtain:
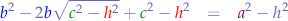
So, by merging the two equations we now have a new equation in  ,
,  ,
,  and
and  and we just need to extract
and we just need to extract  in order to hopefully reduce the equation to Heron's formula.
in order to hopefully reduce the equation to Heron's formula.
Let's collect and get rid of the square root since it's a pain:
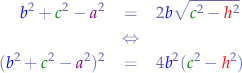
and then let's collect for  :
:
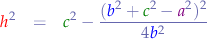
Now let's get to a common denominator:
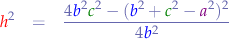
We know that the permitter is expressed as  so we need to shuffle the timers in some form of equation where we can express ourselves in terms of
so we need to shuffle the timers in some form of equation where we can express ourselves in terms of  instead of
instead of  ,
,  and
and  :
:
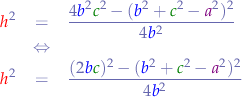
Now, from the rule of polynomials we know that:
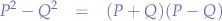
so, we apply that to the nominator, and obtain:
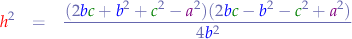
We observe that now we have two second-order polynomials at the denominator:
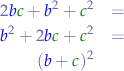
and:
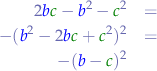
So we can substitute them back into the nominator of the original equation:
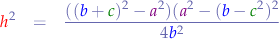
and again, since the polynomial rules says that:
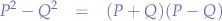
we can expand the nominator further to:
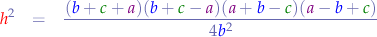
and arrange the terms:

Now we only know that  so we have to do something about the minus (
so we have to do something about the minus (-) signs in order to get to the addition.

and we can substitute  now:
now:

and collect  :
:

Recall that the area of the triangle  can be written as:
can be written as:
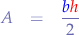
So we can substitute  into that formula:
into that formula:

Now, if you recall Heron's formula, it is expressed as a semi-permitter  instead of
instead of  , so we need to place that
, so we need to place that  inside the square root and distribute it to each of the terms:
inside the square root and distribute it to each of the terms:
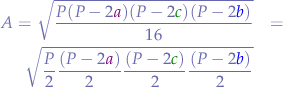
and distribute again:
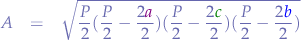
Now we know that the semi-permitter  is
is  so we can substitute it into the formula:
so we can substitute it into the formula:

which is Heron's formula which we had to derive.