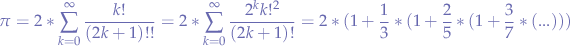Table of Contents
Fibonacci Numbers
The Fibonacci numbers are given by the recurrence relation:
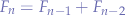
where  and
and  giving the possible sequences:
giving the possible sequences:
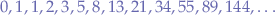
or
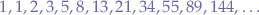
Implementation
Calculating Pi (π)
Fixed Ratio
- Western:
 wrong at the thousandths.
wrong at the thousandths. - Chinese:
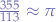 wrong at the ten-millionths.
wrong at the ten-millionths.
Trigonometry

thus:

Newton