Cross Product

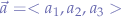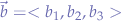The result of the cross-product of a two vectors is another vector. Given two vectors $\vec{a}=<a_{1}, a_{2}, a_{3}>$ and $\vec{b}=<b_{1}, b_{2}, b_{3}>$ , their cross-product can be written as:

$\begin{eqnarray*} \vec{a} \times \vec{b} &=& <a_{2}b_{3}-a_{3}b_{2}, a_{3}b_{1}-a_{1}b_{3}, a_{1}b_{2}-a_{2}b_{1}> \end{eqnarray*}$

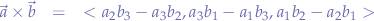
or, using determinants:

$\begin{eqnarray*} \vec{a} \times \vec{b} &=& \left| \begin{matrix} a_{2} & a_{3} \\ b_{2} & b_{3} \end{matrix} \right| i - \left| \begin{matrix} a_{1} & a_{3} \\ b_{1} & b_{3} \end{matrix} \right| j - \left| \begin{matrix} a_{1} & a_{2} \\ b_{1} & b_{2} \end{matrix} \right| k \end{eqnarray*}$

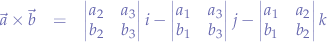
which is derived from:

$\begin{eqnarray*} \vec{a} \times \vec{b} &=& \left| \begin{matrix} i & j & k \\ a_{1} & a_{2} & a_{2} \\ b_{1} & b_{2} & b_{3} \end{matrix} \right| \end{eqnarray*}$

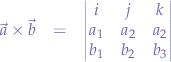
Properties

The length of the resulting vector representing the cross-product of two vectors is:

$\begin{eqnarray*} |\vec{a} \times \vec{b}|&=&|\vec{a}||\vec{b}|\sin{\theta} \end{eqnarray*}$

where the vertical bars represent the scalar value of the vector.

The length of the cross-product of two vectors is equal to the area of the parallelogram determined by the two vectors.

$\begin{tikzpicture} % grid \draw[help lines] (-3,-2) grid (4,2); % origin %\draw[red, line width=.1mm] (-0.1,-0.1) -- (0.1,0.1) % (0.1,-0.1) -- (-0.1,0.1); %\coordinate[label={[red]above:$O$}] (O) at (0,0); %\draw[black,line width=5mm] (-3, {3 * sqrt(3) - sqrt(3)}) -- ((-3,0); %\node [square,rotate={30},minimum size=10mm] at (-3, {3 * sqrt(3) - sqrt(3)}) [draw] (d2) [orange,fill,text=white] {$d_{2}$}; %\draw[orange,line width=.1mm] (-3, {3 * sqrt(3) - sqrt(3)}) -- (-2,0); %\draw[orange,line width=.1mm] (-3, {3 * sqrt(3) - sqrt(3)}) -- (0,2); % coordinates \coordinate[label={[black]left:$A$}] (A) at (-1,1.5); \coordinate[label={[black]left:$B$}] (B) at (-2,-1); \coordinate[label={[black]right:$C$}] (C) at (2,-1); \coordinate[label={[black]right:$D$}] (D) at (3,1.5); \coordinate[label={[black]below:$P$}] (P) at (-1,-1); % mark P \drawpoint{P}{.5mm}{black} % theta \markangle{B}{A}{C}{2mm}{2mm}{$\theta$}{green}{south west} % triangle \draw[black, line width=.1mm] (A) -- (B) -- (C) -- (D) -- cycle; % perpendicular \draw[black, line width=.1mm] (A) -- (P); % alpha \node [square,minimum size=1mm,dotted] at (-1.14,-0.85) [draw] (d2) [black] {}; % braces %\drawbrace{B}{C}{2mm}{blue}{$a$}{0}{-4mm}{mirror} %\drawbrace{A}{P}{2mm}{red}{$h$}{4mm}{0}{} %\drawbrace{A}{B}{2mm}{green}{$c$}{-4mm}{0}{mirror} %\drawbrace{A}{C}{2mm}{red}{$b$}{3mm}{3mm}{} \drawbrace{A}{P}{2mm}{black}{${\color{cyan}|\vec{b}|}\sin{\color{green}{\theta}}$}{10mm}{0mm}{} \drawbrace{B}{C}{2mm}{blue}{$|\vec{a}|$}{0}{-4mm}{mirror} \drawbrace{A}{B}{2mm}{cyan}{$|\vec{b}|$}{-6mm}{2mm}{mirror} \end{tikzpicture}$

$\begin{eqnarray*} A_{\blacksquare} &=& {\color{blue}|\vec{a}|}{\color{cyan}|\vec{b}|}\sin{\color{green}{\theta}} \end{eqnarray*}$

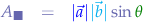
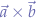Multiplication by scalars is commutative. For example, suppose that $c$ is a scalar and that $\vec{a} \times \vec{b}$ is the cross product of $\vec{a}$ respectively $\vec{b}$ , in that case we have that:

$\begin{eqnarray*} c(\vec{a}) \times \vec{b} &=& \vec{a} \times c(\vec{b}) \end{eqnarray*}$

The cross-product is distributive.

$\begin{eqnarray*} \vec{a} \times (\vec{b} + \vec{c}) &=& \vec{a} \times \vec{b} + \vec{a} \times \vec{c} \end{eqnarray*}$

The volume of the parallelepiped determined by the vectors $\vec{a}$ , $\vec{b}$ and $\vec{c}$ is equal to the magnitude of their scalar triple product.

The vector triple product of the vectors $\vec{a}$ , $\vec{b}$ and $\vec{c}$ is given by:

$\begin{eqnarray*} \vec{a} \times (\vec{b} \times \vec{c}) &=& (\vec{a} \cdot \vec{c})\vec{b} - (\vec{a} \cdot \vec{b})\vec{c} \end{eqnarray*}$

Two vectors are parallel if and only if their cross product is the zero vector.

Determining Triangle Area in Three Dimensions

One solution to find the area of a triangle is to determine its height and then proceed to the multiply the height by the base and divide by two. However, that may be a difficult task and instead, by using the parallelogram property of vectors, one can calculate the area of the parallelogram and then divide the area by two.

Table of Contents

Cross Product

Properties

Determining Triangle Area in Three Dimensions