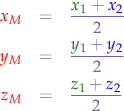Table of Contents
Equation of a Line
Standard
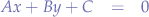
where:
- the slope of the line is

- the y-intercept is

Given two points 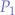 and
and  on the line, we can write that:
on the line, we can write that:
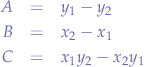
in order to determine  ,
,  and
and  .
.
Slope-Intercept
![LaTeX
\begin{tikzpicture}
% grid
\draw[help lines] (-2,-2) grid (2,2);
% origin
\draw[red, line width=.1mm] (-0.1,-0.1) -- (0.1,0.1)
(0.1,-0.1) -- (-0.1,0.1);
\coordinate[label={[red]above left:$O$}] (O) at (0,0);
\coordinate[label={[red]above left:$A$}] (A) at (-2,0);
\drawpoint{A}{.5mm}{black}
\coordinate[label={[red]above left:$B$}] (B) at (2,1);
\drawpoint{B}{.5mm}{black}
\draw (A) -- (B);
\coordinate (C) at (2,0);
\coordinate (D) at (0,1);
\draw[dotted,->] (O) -- (C) node[below] {$x$};
\draw[dotted,->] (O) -- (D) node[left] {$y$};
\markangle{A}{B}{C}{3mm}{3mm}{$\alpha$}{cyan}{north}
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/img1db7cd7cc685fc1ec9425cf7a1bb5628.png)

where  is the slope:
is the slope:

where  is the angle between the line and the
is the angle between the line and the  axis.
axis.
 can also be expressed parametrically as:
can also be expressed parametrically as:
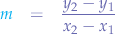
where  are the components of the points
are the components of the points 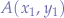 and
and 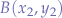 of the line.
of the line.
Point-Slope
Given two points 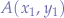 and
and 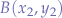 and a connecting line
and a connecting line  , the point-intercept form of the line is given by:
, the point-intercept form of the line is given by:

where  is the slope of the line.
is the slope of the line.
Parametric Form
In parametric form:

where:
 is a generic point on the line.
is a generic point on the line.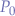 is the starting point of the line segment.
is the starting point of the line segment.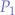 is the end point of the line segment.
is the end point of the line segment. is a parameter with
is a parameter with ![Math $t: \mathbb{R} \mapsto [0, 1]$](/lib/exe/fetch.php?media=wiki:latex:/img97602d21575ab17fc25e07141208a5cb.png) where by taking values and working out the equation yields points on the line.
where by taking values and working out the equation yields points on the line.
Midpoint of a Segment
![LaTeX
\begin{tikzpicture}
% grid
\draw[help lines] (-2,-2) grid (2,2);
% origin
\draw[black, line width=.1mm] (-0.1,-0.1) -- (0.1,0.1)
(0.1,-0.1) -- (-0.1,0.1);
\coordinate[label={[black]below left:$O$}] (O) at (0,0);
\coordinate[label={[green]above left:$A(x_{1}, y_{1}, z_{1})$}] (A) at (-2,0);
\drawpoint{A}{.5mm}{black}
\coordinate[label={[blue]above left:$B(x_{2}, y_{2}, z_{2})$}] (B) at (2,1);
\drawpoint{B}{.5mm}{black}
\draw (A) -- (B);
\coordinate[label={[red]above left:$M$}] (M) at (0,0.5);
\drawpoint{M}{.5mm}{red}
\coordinate (C) at (2,0);
\coordinate (D) at (0,2);
\draw[dotted,->] (O) -- (C) node[below] {$x$};
\draw[dotted,->] (O) -- (D) node[left] {$y$};
%\markangle{A}{B}{C}{3mm}{3mm}{$\alpha$}{cyan}{north}
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/imgb9939990a47b21049bb026292ecbfe15.png)
Knowing the components of two points  and
and  , we can determine the midpoint
, we can determine the midpoint  of the segment
of the segment  whose components are:
whose components are: