Circle Area and Perimeter
![\begin{tikzpicture}
% grid
\draw[help lines] (-2,-2) grid (2,2);
% origin
\draw[red, line width=.1mm] (-0.1,-0.1) -- (0.1,0.1)
(0.1,-0.1) -- (-0.1,0.1);
\coordinate[label={[red]above left:$O$}] (O) at (0,0);
\coordinate[label={[red]above right:$R$}] (R) at (2,0);
\coordinate[label={[red]above right:$Q$}] (Q) at (0,2);
\coordinate[label={[red]above right:$C$}] (C) at (2,2);
%radius
\draw[fill=blue!20,fill opacity=0.1] (O) -- (R) -- (C) -- (Q) -- cycle;
% triangle
\draw [black] (0,0) circle [radius=2];
\drawbrace{O}{R}{2mm}{blue}{$r$}{0}{-4mm}{mirror};
\node [thick] at (1,1) {$A_{\square}=r^{2}$};
\node [thick] at (0,-1) {$A_{\bullet}=\pi*r^{2}$};
\node [thick] at (0,-1.5) {$P_{\bullet}=2*\pi*r$};
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/imgae84c5a9df80054c24391c0d79854eda.png "LaTeX")
A circle contains the maximal surface in relation to its perimeter. This translates to spheres as well, since a sphere contains the maximal volume in relation to its surface.
Equation of a Circle
![\begin{tikzpicture}
% grid
\draw[help lines] (-2,-2) grid (2,2);
% origin
\draw[red, line width=.1mm] (-0.1,-0.1) -- (0.1,0.1)
(0.1,-0.1) -- (-0.1,0.1);
\coordinate[label={[red]above left:$O$}] (O) at (0,0);
\coordinate[label={[red]above right:$R$}] (R) at (2,0);
\coordinate[label={[red]above right:$Q$}] (Q) at ({cos(30)},{2*cos(30)});
%projection
\draw[black,dotted] (Q) -- ({cos(30)},0);
\node [square,minimum size=1mm,dotted] at ({cos(30)-0.1},0.1) [draw] (d2) [black] {};
\drawpoint{Q}{.5mm}{red};
%radius
%\draw[fill=blue!20,fill opacity=0.1] (O) -- (R);
% circle
\draw [black] (0,0) circle [radius=2];
\draw [black] (O) -- (R);
\draw [black] (O) -- (Q);
\drawbrace{O}{R}{2mm}{blue}{$r$}{0}{-4mm}{mirror};
\drawbrace{O}{Q}{2mm}{blue}{$r$}{-4mm}{0}{};
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/img5958f08ff39c311523ef56f2bcb13bd4.png "LaTeX")
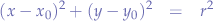
where the parameters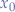 
and 
represent an offset from the origin point 
(usually both equal to zero if the circle is centred in the origin point).