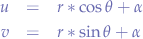Table of Contents
Conversion Between Cartesian, Cylindrical and Spherical Coordinates
| Coordinate System | Notation |
|---|---|
| Cartesian | 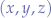 |
| Cylindrical | 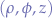 |
| Spherical | 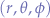 |
Cartesian to Cylindrical
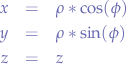
Cylindrical to Cartesian
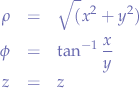
Cartesian to Spherical
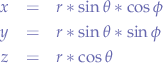
Spherical to Cartesian
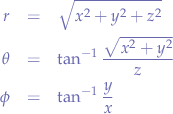
Rotation of a Point along an Arc
The task is to rotate a point 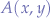 along an arc described by an angle
along an arc described by an angle  . In order to do that, we express the point
. In order to do that, we express the point  in polar coordinates:
in polar coordinates:
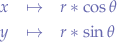
Then, rotating by angle  in the trigonometric sense (counter-clockwise) will change the angle
in the trigonometric sense (counter-clockwise) will change the angle  and leave
and leave  unchanged giving us the new point
unchanged giving us the new point 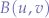 , where:
, where: