Intersection Between Two Segments Given Four Points
![LaTeX
\begin{tikzpicture}
% grid
\draw[help lines] (-2,-2) grid (2,2);
% origin
\draw[black, line width=.1mm] (-0.1,-0.1) -- (0.1,0.1)
(0.1,-0.1) -- (-0.1,0.1);
\coordinate[label={[black]below left:$O$}] (O) at (0,0);
\coordinate[label={[cyan]above left:$A$}] (A) at (-2,0);
\drawpoint{A}{.5mm}{cyan}
\coordinate[label={[blue]above left:$B$}] (B) at (2,1);
\drawpoint{B}{.5mm}{blue}
\coordinate[label={[green]above left:$C$}] (C) at (-1,1);
\drawpoint{C}{.5mm}{green}
\coordinate[label={[brown]above right:$D$}] (D) at (2,-1);
\drawpoint{D}{.5mm}{brown}
\draw (A) -- (B);
\draw (C) -- (D);
% median for A
\path[draw, black, line width=.1mm, solid, name path=median from A] (A) -- (B);
% median for B
\path[draw, black, line width=.1mm, solid, name path=median from C] (C) -- (D);
% gravity centre
\path[draw, red, name intersections={of=median from A and median from C, by=I}];
\drawpoint{I}{.5mm}{red}
\coordinate[label={[red]above:$I$}] (I) at (I);
%\coordinate (C) at (2,0);
%\coordinate (D) at (0,1);
%\draw[dotted,->] (O) -- (C) node[below] {$x$};
%\draw[dotted,->] (O) -- (D) node[left] {$y$};
%\markangle{A}{B}{C}{3mm}{3mm}{$\alpha$}{cyan}{north}
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/img8b55977f584adfaa3dfeb60711c1d9d9.png)
Given four points with known coordinates:
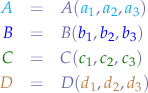
Writing the parametric equation for the line  :
:
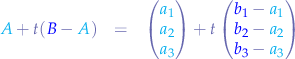
and the parametric equation for the line  :
:
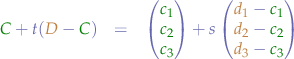
with  and
and  . Notice that if
. Notice that if  then we get the starting point of line
then we get the starting point of line  and if
and if  then we get the ending point of line
then we get the ending point of line  . Symmetrically, the same applies to
. Symmetrically, the same applies to  , giving the start point of segment
, giving the start point of segment  and
and  , giving the end point of segment
, giving the end point of segment  .
.
Equating the two equations for lines  and
and  , we obtain the system of linear equations:
, we obtain the system of linear equations:
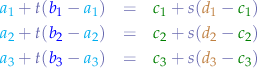
We determine  and
and  from the first two equations:
from the first two equations:
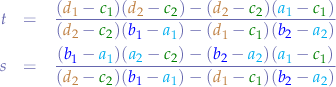
Note that the denominator, call it  :
:
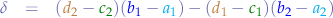
is the same for both  and
and  .
.
Judging on cases, we can say that:
- if
 then the segments do not intersect,
then the segments do not intersect, - if
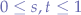 and the third equation is satisfied by
and the third equation is satisfied by  and
and  , then the lines intersect at the point
, then the lines intersect at the point  , with the coordinates:
, with the coordinates:
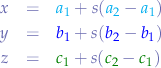
Implementation
The vectors A, B, C and D are given in parametric form, for example:
vector A = <34.517483, 231.703461, 21.108919>; vector B = <34.517483, 222.014297, 21.108919>; vector C = <29.423143, 226.800842, 21.108919>; vector D = <38.186848, 226.800842, 21.108919>;
In order to determine whether the segments  and
and  intersect, one would call the function as:
intersect, one would call the function as:
if(wasSegmentIntersect(A, B, C, D) == TRUE) { llOwnerSay("Segments AB and CD intersect."); return; } llOwnerSay("Segments AB and CD do not intersect.");
wasSegmentIntersect is defined as:
/////////////////////////////////////////////////////////////////////////// // Copyright (C) 2014 Wizardry and Steamworks - License: GNU GPLv3 // /////////////////////////////////////////////////////////////////////////// // determines whether the segment AB intersects the segment CD integer wasSegmentIntersect(vector A, vector B, vector C, vector D) { vector s1 = <B.x - A.x, B.y - A.y, B.z - A.z>; vector s2 = <D.x - C.x, D.y - C.y, D.y - C.z>; float d = (s1.x * s2.y -s2.x * s1.y); if(d == 0) return FALSE; float s = (s1.x * (A.y - C.y) - s1.y * (A.x - C.x)) / d; float t = (s2.x * (A.y - C.y) - s2.y * (A.x - C.x)) / d; // intersection at <A.x + (t * s1.x), A.y + (t * s1.y), A.z + (t * s1.z)>; return (integer)(s >= 0 && s <= 1 && t >= 0 && t <= 1 && A.z + t*(B.z - A.z) == C.z + s*(D.z - C.z)); }