Intersection Between a Plane and a Segment
![LaTeX
\begin{tikzpicture}
% grid
\draw[help lines] (-4,-3) grid (5,4);
% origin
%\draw[red, line width=.1mm] (-0.1,-0.1) -- (0.1,0.1)
% (0.1,-0.1) -- (-0.1,0.1);
%\coordinate[label={[red]above:$O$}] (O) at (0,0);
%\draw[black,line width=5mm] (-3, {3 * sqrt(3) - sqrt(3)}) -- ((-3,0);
%\node [square,rotate={30},minimum size=10mm] at (-3, {3 * sqrt(3) - sqrt(3)}) [draw] (d2) [orange,fill,text=white] {$d_{2}$};
%\draw[orange,line width=.1mm] (-3, {3 * sqrt(3) - sqrt(3)}) -- (-2,0);
%\draw[orange,line width=.1mm] (-3, {3 * sqrt(3) - sqrt(3)}) -- (0,2);
% coordinates
\coordinate[label={[black]left:$A$}] (A) at (-1,1.5);
\coordinate[label={[black]left:$B$}] (B) at (-2,-1);
\coordinate[label={[black]right:$C$}] (C) at (2,-1);
\coordinate[label={[black]right:$D$}] (D) at (3,1.5);
\coordinate[label={[black]left:$P_{0}$}] (P0) at (-.5,-2);
\coordinate[label={[black]right:$P_{1}$}] (P1) at (1,2.5);
\coordinate (R) at (-.15,-1);
\coordinate[label={[black]right:$I$}] (I) at (.35,.5);
\coordinate (N) at (.35, 3);
% plane
\draw[black, line width=.1mm] (A) -- (B) -- (C) -- (D) -- cycle;
% mark points
\drawpoint{P0}{.5mm}{black};
\drawpoint{I}{.5mm}{black};
\drawpoint{P1}{.5mm}{black};
% line
\draw[black, line width=.1mm] (P0) -- (R);
\draw[dotted, black, line width=.1mm] (R) -- (I);
\draw[black, line width=.1mm] (I) -- (P1);
% normal
\draw[->, black, line width=.1mm] (I) -- (N);
% brace normal
\drawbrace{I}{N}{2mm}{cyan}{$\vec{n}$}{-6mm}{2mm}{}
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/imga9cce69461c17c2e7977e8e330a54ca5.png)
The segment may  intersect the plane formed by
intersect the plane formed by  with the normal
with the normal  in any (or all) generic point
in any (or all) generic point  on the segment.
on the segment.
The line equation in parametric form can be expressed as:

where  is the intersection between the segment
is the intersection between the segment  and the plane
and the plane  and values of
and values of  will yield points on that segment.
will yield points on that segment.
The equation of the plane can be expressed as:

where  can be any known point in the plane
can be any known point in the plane  .
.
We plug the line equation into the equation of the plane:
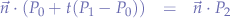
and distribute the normal vector  :
:

then collect for  :
:

then group on the right-hand side of the equation:
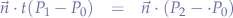
and collect again for  we obtain the equation for
we obtain the equation for  :
:
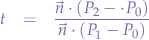
Now, based on the equation, we can make the following judgments:
- We know from the vector properties that if
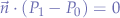 then the vector
then the vector  and the segment
and the segment  are perpendicular meaning that the segment
are perpendicular meaning that the segment  is either parallel to the plane formed by
is either parallel to the plane formed by  or that the segment
or that the segment  is contained entirely in the plane described by
is contained entirely in the plane described by  .
.- If any point on the segment
 is contained in the plane described by
is contained in the plane described by  then the entire segment is contained within the plane.
then the entire segment is contained within the plane. - If any point on the segment
 is contained in the plane described by
is contained in the plane described by  then the segment is parallel with the plane described by
then the segment is parallel with the plane described by  .
.
- If
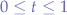 then the segment
then the segment  interesects the plane.
interesects the plane.- If
 then the intersection falls on the first end-point.
then the intersection falls on the first end-point. - If
 then the intersection falls on the second end-point.
then the intersection falls on the second end-point.
- If
 or
or  then the segment
then the segment  does not intersect the plane.
does not intersect the plane.- If
 then intersection occurs beyond the second end-point.
then intersection occurs beyond the second end-point. - If
 then intersection occurs before the first end-point.
then intersection occurs before the first end-point.