Table of Contents

Polynomial Expansions

\begin{eqnarray*} (x+y)^{2} &=& x^2 + y^2 + x*y & \\ (x+y)^{3} &=& x^{3}+3*x^{2}*y+3*x*y^{2}+y^{3} \end{eqnarray*}

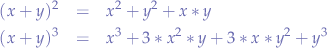
Binomial Formula

(x+y)^{n} &=& C_{0}^{n}{x}y^{0}+C_{1}^{n}{x}{y}+C_{2}^{n}{x}y^{2} + ... + C_{n}^{n-1}{x^1}{y^{n-1}}+C_{n}^{n}x^{0}y^{n}

Implementations

Linearly Map a Value in a Range into another Range

Given a value $s$ such that $s \in [a_{1},a_{2}]$ we can map $s$ onto a different range such that $s \in [b_{1}, b_{2}]$ by using the formula:

\begin{eqnarray*} t &=& b_{1} + \frac{(s-a_{1})(b_{2}-b_{1})}{a_{2}-a_{1}} \end{eqnarray*}

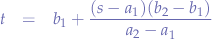
Implementations

Invert a Range

Given a range $A$ represented as an ordered set $A=\{ x_{i} \mid i=\vert 1..n \vert, x_{i} \in A \}$, the inverted-range ordered set $B$ is obtained using the formula $max(A) - A_{i} + min(A)$ such that $B=\{ y_{i} \mid i=\vert 1..n \vert, y_{i}=max(A) - A_{i} + min(A) \}$ where $max$ is a function that returns the largest element in a set.

Or, in other words, the set $B$ is the sequential union of all elements $B_{i}$ obtained via the formula $max(A) - A_{i} + min(A)$ as follows:

\begin{eqnarray*} \bigcup_{i=1}^n B_{i} = \{ max(A) - A_{i} + min(A) \mid A_{i} \in A \} \end{eqnarray*}

Clamp a Random Number to a Range

Given an arbitrary random number $r:X \mapsto Y$, in order to obtain a random number $\rho$ such that $\rho \in [min, max], \rho:X \mapsto [min, max]$ and notice that $\rho \subseteq Y$, the following formula can be used:

\begin{eqnarray*} \rho_{[min,max]} = min + r \% ( max - min + 1 ) \end{eqnarray*}

where: