Table of Contents
op0p;
Take
take is a general aggregator over a data set that returns the first  items of a list.
items of a list.
Lambda Calculus
Take can be expressed in lambda calculus as a RANGE function where parameter s is 0 and e is the amount of items to retrieve from a list:
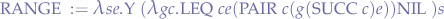
using the following definitions:

where the variable  is set to:
is set to:
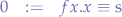
and  is a parameter that can be set to the number of items to retrieve from the start of the list.
is a parameter that can be set to the number of items to retrieve from the start of the list.
TODO: derive  from
from  by reducing
by reducing
JavaScript
var items = array.slice(0, n);