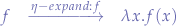Table of Contents
Implementing the Y-Combinator
Curry defines the 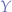 -combinator as:
-combinator as:

which, when applied to a lambda term  ,
,  -reduces in two steps to:
-reduces in two steps to:

An equivalent  -combinator definition is the following:
-combinator definition is the following:

which consists of part of the  combinator
combinator  named
named 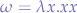 and the term
and the term 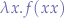 .
.
If we  -reduce the equivalent form once:
-reduce the equivalent form once:

we would obtain Curry's form of the 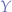 -combinator.
-combinator.
Whilst the Curry form should work perfectly fine in Scheme and untyped lambda calculus, a statically typed language will not accept a function application such as  since the type system will forbid it. In order to do that, we start by applying an additional
since the type system will forbid it. In order to do that, we start by applying an additional  -abstraction to obtain the form:
-abstraction to obtain the form:

which can be re-written as:
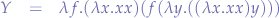
We notice that the  combinator (
combinator ( ) appears twice in the resulting
) appears twice in the resulting 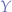 -combinator which lets us express the
-combinator which lets us express the 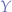 -combinator using the
-combinator using the  combinator:
combinator:
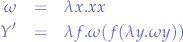
where  and
and 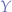 are
are  -equivalent.
-equivalent.
Expressing the 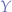 combinator in terms of
combinator in terms of  allows us to implement the
allows us to implement the 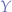 combinator in statically typed programming languages.
combinator in statically typed programming languages.
Implementations
Exponentiation with Church Numerals
You may have seen the definition of exponentiation as the combinator 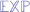 (or
(or  ) given by the lambda abstraction:
) given by the lambda abstraction:

where  and
and  are both Church numerals.
are both Church numerals. 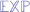 will perform the mathematical equivalent of
will perform the mathematical equivalent of 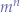 using Church numerals.
using Church numerals.
Therefore the application of a Church numeral  to another Church numeral
to another Church numeral  will yield the Church numeral equivalent to
will yield the Church numeral equivalent to 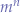 . For instance, applying the Church numeral
. For instance, applying the Church numeral  to Church numeral
to Church numeral  should yield
should yield 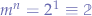 . While all the numerals work out, the application of the Church numeral zero to any other Church numeral
. While all the numerals work out, the application of the Church numeral zero to any other Church numeral  -reduces to the identity function
-reduces to the identity function  . For instance, applying the Church numeral
. For instance, applying the Church numeral  to
to  we have:
we have:

Since the identity function  is not a Church numeral, it would seem that the application is not defined. However, by the rules of exponentiation, any number to the power zero should yield one; in other words:
is not a Church numeral, it would seem that the application is not defined. However, by the rules of exponentiation, any number to the power zero should yield one; in other words: 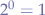 .
.
The trick here is that the identity function  is equivalent with the Church numeral
is equivalent with the Church numeral  under the
under the  -expansion.
-expansion.
The  -expansion is given by:
-expansion is given by:
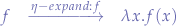
so we can re-work the application of the Church numeral zero to the Church numeral two:
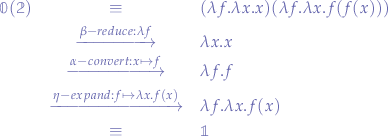
which yields the expected result.
η-Reduction and η-Expansion
 -reduction is given by:
-reduction is given by:

 -expansion is given by:
-expansion is given by: