Table of Contents
Von-Neumann Debiasing
Von-Neumann debiasing can be used to remove entropy bias from a sequence of random or pseudo-random binary digits using a simple algorithm.
Given the set of binary digits:
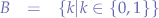
and  a sequence of arbitrary binary digits:
a sequence of arbitrary binary digits:
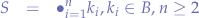
Let 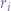 be a debiased random binary number such that:
be a debiased random binary number such that:
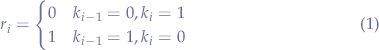
The following table shows the possible outcomes for the random binary digit 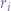 :
:
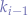 |  | 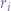 |
|---|---|---|
| 0 | 0 | discard |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | discard |
Exercises
Definition of a Line of Text
A line of text is defined by POSIX as:
3.206 Line
A sequence of zero or more non-<newline> characters plus a terminating <newline> character.
Regular Expression:
/^[^\n]+?$/gm
where the following regular expression engine modifiers have to be set:
gis a greedy flag (in order to match all the lines in a document),mis a multi-line match flag
Due to the definition many programs and environments (for example, the LSL programming language) processing the last line in a text file iff. the last line is not terminated by a newline character.
The Empty String, List, Queue, Etc...
One confusing concept to non-computer science majors is the concept behind the expression "the empty string", or "the empty list", or "the empty queue". These expressions are the closest to mathematics when defined.
All variables are considered from a memory model perspective containers and that types are qualifiers for those containers. In that sense, "the empty O" where "O" is a type, refers to a container of a given type that currently has nothing stored inside. With collections and co-variance, the concepts become more complex where variables refer to containers and then those containers, in turn, can be empty.
The following definitions can then be constructed:
- an empty string is a string container that contains zero characters and is referred to by a given variable
- on a technical layer zero characters could be represented by a single end-of-string character
\0, or perhaps by setting all the allocated memory to zero,
- an empty list is a list container that contains zero element
- on a technical layer, usually a list contains a counter of its internal size (ie: for linked lists), which in the case that the list is empty, should be zero
- bear in mind that if lists are to be considered sets, then a set
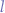 such that
such that  is still a valid set containing nothing
is still a valid set containing nothing
Object-oriented programming makes theoretical computer science more perceivable at the level of code, where objects are synonymous with types, such that a "string", "list" / "set", "queue", etc, will greatly exceed their memory-model conceptualization and will tend to be closer to their mathematical abstraction. Pragmatic programming languages tend to blur the understanding that variables are nothing more than containers when it comes to data.