Table of Contents
About
As described on the polygon point generator page, the following script generates a point within a polygon by using an encompassing minimal ellipse to generate the points and then applying a select-reject algorithm to those generated points.
Compared to the similar algorithm that uses a circle generator, this algorithm is more efficient since it reduces the reject area by using an encompassing ellipse.
Algorithm
In order to determine the minimal-enclosing ellipse of any given polygon, the following operations should be performed:
- given all the points defining the perimeter of the polygon, determine the largest segment that can be created between any two pairs of points and call this segment
a. - given all the points defining the permitter of the polygon, determine the smallest segment that can be created between any two pairs of points and call this segment
b. - half of the segment
awill be the large radius of the ellipse and the segmentbwill be the small start radius. - generate ellipses by taking half of
aas the large radius and increase the length ofbuntil one ellipse encloses all the points of the polygon. - the smallest enclosing ellipse will thus be an ellipse with the centre at the middle of segment
a, with the large radius being half ofaand the small radius the determinedb.
Implementation
The implementation is made to re-calculate the minimal encompassing ellipse every time that the function wasPolygonPoint is called. A consequence of this is that you can actually change the polygonPoints list and supply it as a parameter to wasPolygonPoint, at which point the algorithm will adapt to the new shape of the polygon generated by those points.
However, in case the polygon points do not change (or change rarely), then the script can be changed to store all the calculated variables (the place is marked in the script) and just generate points within the computed ellipse. This will drastically speed-up the algorithm at the cost that the polygonPoints list of points will not change until after a script restart.
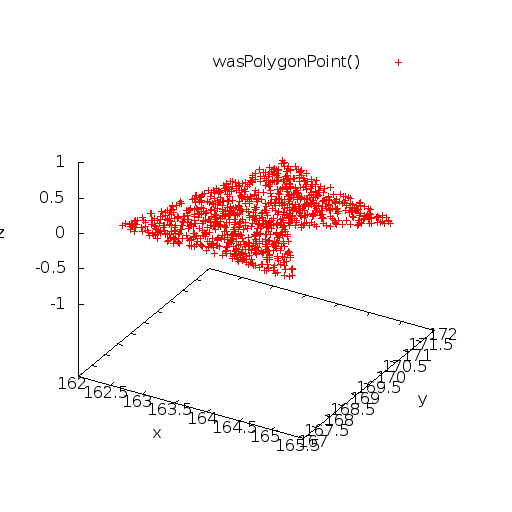
Graph
Code
- wasPolygonPoint.lsl
/////////////////////////////////////////////////////////////////////////// // Copyright (C) 2015 Wizardry and Steamworks - License: GNU GPLv3 // /////////////////////////////////////////////////////////////////////////// vector wasEllipsePoint(float a, float b) { float x = llPow(-1, 1 + (integer) llFrand(2)) * llFrand(a); float y = llPow(-1, 1 + (integer) llFrand(2)) * llFrand(b); if(llPow(x/a,2) + llPow(y/b,2) <= 1) return <x, y, 0>; return wasEllipsePoint(a, b); } /////////////////////////////////////////////////////////////////////////// // Copyright (C) 2015 Wizardry and Steamworks - License: GNU GPLv3 // /////////////////////////////////////////////////////////////////////////// // the angle (in radians) o represents a rotation in the trigonometric // sense around the Ox axis where O represents the ellipse center vector wasRotatedEllipsePoint(float a, float b, float o) { float x = llPow(-1, 1 + (integer) llFrand(2)) * llFrand(a); float y = llPow(-1, 1 + (integer) llFrand(2)) * llFrand(b); if(llPow(x/a,2) + llPow(y/b,2) <= 1) return <x*llCos(o) + y*llSin(o), x*llSin(o)-y*llCos(o), 0>; return wasRotatedEllipsePoint(a, b, o); } /////////////////////////////////////////////////////////////////////////// // Copyright (C) 2015 Wizardry and Steamworks - License: GNU GPLv3 // /////////////////////////////////////////////////////////////////////////// // given a set of points, determines the largest segment that can be // created between any of those points list wasLargestSegment(list points) { list dists = []; list xi = []; list xj = []; integer i = llGetListLength(points) - 1; do { integer j = llGetListLength(points) - 1; do { if(i == j) jump continue; float d = llVecDist( llList2Vector(points, j), llList2Vector(points, i) ); dists += d; xi += i; xj += j; @continue; } while(--j > -1); } while(--i > -1); i = llGetListLength(dists) - 1; float d = llList2Float(dists, i); --i; integer x = 0; integer y = 0; do { float t = llList2Float(dists, i); if(d < t) { x = llList2Integer(xi, i); y = llList2Integer(xj, i); d = t; } } while(--i > -1); return [llList2Vector(points, x), llList2Vector(points, y)]; } /////////////////////////////////////////////////////////////////////////// // Copyright (C) 2015 Wizardry and Steamworks - License: GNU GPLv3 // /////////////////////////////////////////////////////////////////////////// // given a set of points, determines the smallest segment that can be // created between any of those points list wasSmallestSegment(list points) { list dists = []; list xi = []; list xj = []; integer i = llGetListLength(points) - 1; do { integer j = llGetListLength(points) - 1; do { if(i == j) jump continue; float d = llVecDist( llList2Vector(points, j), llList2Vector(points, i) ); dists += d; xi += i; xj += j; @continue; } while(--j > -1); } while(--i > -1); i = llGetListLength(dists) - 1; float d = llList2Float(dists, i); --i; integer x = 0; integer y = 0; do { float t = llList2Float(dists, i); if(d > t) { x = llList2Integer(xi, i); y = llList2Integer(xj, i); d = t; } } while(--i > -1); return [llList2Vector(points, x), llList2Vector(points, y)]; } /////////////////////////////////////////////////////////////////////////// // Copyright (C) 2015 Wizardry and Steamworks - License: GNU GPLv3 // /////////////////////////////////////////////////////////////////////////// // takes two points defining a segment and returns the angle created // between the Ox axis and the segement (the angle will be positive for the // trigonometric quadrants I and II and negative for III and IV) float wasOXSegmentAngle(vector A, vector B) { float alpha = llAtan2( llVecDist( B, <B.x, A.y, 0> ) / llVecDist( A, <B.x, A.y, 0> ), 1 ); if(B.y < A.y) return -alpha; return alpha; } /////////////////////////////////////////////////////////////////////////// // Copyright (C) 2015 Wizardry and Steamworks - License: GNU GPLv3 // /////////////////////////////////////////////////////////////////////////// // takes a set of points describing a polygon and returns the radiuses of // the minimal ellipse that encloses all the points of the polygon list wasMinimalPolygonEllipse( list points, vector C, float a, float b, float angle, float increment ) { integer i = llGetListLength(polygonPoints)-1; do { vector p = llList2Vector(polygonPoints, i); if(llPow( ( (p.x-C.x)*llCos(a)+(p.y-C.y)*llSin(a) )/a, 2 ) + llPow( ( (p.x-C.x)*llSin(a)-(p.y-C.y)*llCos(a) )/b, 2) <= 1) jump continue; b += increment; return wasMinimalPolygonEllipse(points, C, a, b, angle, increment); @continue; } while(--i>-1); return [a, b]; } /////////////////////////////////////////////////////////////////////////// // Copyright (C) 2013 Wizardry and Steamworks - License: GNU GPLv3 // // www.ecse.rpi.edu/Homepages/wrf/Research/Short_Notes/pnpoly.html // /////////////////////////////////////////////////////////////////////////// integer wasPointInPolygon(vector p, list polygon) { integer inside = FALSE; integer i = 0; integer nvert = llGetListLength(polygon); integer j = nvert-1; do { vector pi = llList2Vector(polygon, i); vector pj = llList2Vector(polygon, j); if ((pi.y > p.y) != (pj.y > p.y)) if(p.x < (pj.x - pi.x) * (p.y - pi.y) / (pj.y - pi.y) + pi.x) inside = !inside; j = i++; } while(i<nvert); return inside; } /////////////////////////////////////////////////////////////////////////// // Copyright (C) 2015 Wizardry and Steamworks - License: GNU GPLv3 // /////////////////////////////////////////////////////////////////////////// // takes as input the points describing a polygon and returns a point // within the polygon // // note that this function allows to dynamically change the polygon points // and will adjust to the newly specified polygon if the list has changed // otherwise, consider calculating all the variables within the marked // blocks only once and storing them since the performance will improve! vector wasPolygonPoint(list polygon) { ////////////////// CAN BE CALCULATED ONLY ONCE //////////////////////// ///////////////// AND STORED IN GLOBAL VARIABLES ////////////////////// // Get the largest segment. list largeSegment = wasLargestSegment(polygonPoints); vector A = llList2Vector(largeSegment, 0); A.z = 0; vector B = llList2Vector(largeSegment, 1); B.z = 0; // Get the center of the largest segement. vector C = <(A.x + B.x)/2, (A.y + B.y)/2, 0>; // Get the size of the largest segment. float largeSegmentSize = llVecDist(A, B); // Get the angle between 0x and the segment float a = wasOXSegmentAngle(A, B); // Get the smallest segment. list smallSegement = wasSmallestSegment(polygonPoints); // Get the size of the smallest segment. float smallSegmentSize = llVecDist( llList2Vector(smallSegement, 0), llList2Vector(smallSegement, 1) ); // Now find the minimal ellipse around the polygon. list m = wasMinimalPolygonEllipse( polygonPoints, C, largeSegmentSize, smallSegmentSize, a, 0.1 ); ////////////////// CAN BE CALCULATED ONLY ONCE //////////////////////// ///////////////// AND STORED IN GLOBAL VARIABLES ////////////////////// vector d = ZERO_VECTOR; do { d = C + wasRotatedEllipsePoint(llList2Float(m, 0), llList2Float(m, 1), a); } while(wasPointInPolygon(d, polygon) == FALSE); return d; } /////////////////////////////////////////////////////////////////////////// // these points represent the coordinates of the points that define the // // contour (permimeter) of the polgyon // /////////////////////////////////////////////////////////////////////////// list polygonPoints = [ <163.349121, 171.559189, 3400.894287>, <165.56424, 170.422821, 3400.894287>, <164.364594, 169.194382, 3400.894287>, <165.171875, 167.453903, 3400.894287>, <162.345123, 167.61731, 3400.894287>, <163.349121, 171.659189, 3400.894287> ]; default { state_entry() { integer i = 1000; do { llOwnerSay((string)wasPolygonPoint(polygonPoints)); } while(--i > -1); } }