Introduction

Differently from other programming languages, LSL exposes the concept of states on the upper layers of the language semantics. That is, we are able to explicitly define and observe states as being a construct within the syntax of the language itself. Whereas, before, states were a substructural part of the language semantics, in LSL we have the capability to observe and directly manipulate those states by using the state statement and transitioning to any labeled state.

As an example, we can show the way these state-transitions are written in LSL:

state default
{
  state_entry() {
    state a;
  }
}
state a {
  state_entry() {
    state b;
  }
}
state b {
  state_entry() {
    state default;
  }
}

Each state in LSL marks an un-typed label, encasing a block of code that may be executed once a jump is performed to that particular state. Contrasting with jump labels, in LSL every state may subscribe to global events and process them internally. There is no possible return from one state to the other unless another jump is performed by using the state command.

This gives the language the possibility of two types of continuations: one in the automata interpretation where a transition is made from state to state, and other interpretation where jumps are performed using labels. However, one must note, that at the time of writing the jump labels are locally-scoped to the state or function they are used inside and do not have a global scope. Symmetrically state-transitions are globally scoped, with the exception that state transitions may not be performed within the body of any user-defined function and are restricted to any event body that the state subscribes to.

NFA

In principle, every LSL script is a non-deterministic finite automata (NFA) with any amount of possible user-defined states. One may perform a conditional transition from state to state by using the state command. The default "Hello, World!" script created by Linden Labs. as the default script template whenever a new script is created, has just one state, called the default state.

default
{
    state_entry()
    {
        llSay(0, "Hello, Avatar!");
    }
 
    touch_start(integer total_number)
    {
        llSay(0, "Touched.");
    }
}

Formally, an NFA is expressed as a 5-tuple $(Q, \Sigma, \Delta, q_{0}, F)$ , composed of:

a finite set of states $Q$
a finite set of input symbols $\Sigma$
a transition relation $\Delta : Q \times \Sigma \mapsto P(Q)$ .
an initial starting state $q_{0} \in Q$
a set of states $F$ distinguished as final states $F \subseteq Q$ .

Where, commonly, a state transition relation $\Delta$ can be defined by a state transition table.

Probabilistic Automata

We present a weighted non-deterministic automata where each jump from one state to another is conditioned by a weight with a user-defined probability. We thus obtain something we call a Weighted Non-deterministic Finite Automata (wNFA) which can be derived from an NFA.

$\begin{tikzpicture}[->,>=stealth',shorten >=1pt,auto,node distance=2.8cm, semithick] \tikzstyle{every state}=[fill=red,draw=none,text=white] \node[initial,state] (A) {$default$}; \node[state] (B) [right of=A] {$a$}; \node[state] (C) [right of=B] {$b$}; \node[state] (D) [right of=C] {$c$}; \path (A) edge node {80\%} (B) (B) edge node {100\%} (C) (C) edge node {100\%} (D) (C) edge [loop below] node {100\%} (C); \draw (D) to [out=-100,in=-50] node {100\%} (B); \draw (A) to [out=100,in=100] node {20\%} (D); \draw (C) to [out=100,in=100] node {50\%} (A); \end{tikzpicture}$

Compared to the classic automata, the transition relation for the wNFA contains weights for every transition. If you will, this compares to the classical NFA, in that the state transition table is not two-dimensional but rather three-dimensional containing s series of probabilities for each state transition.

For example, looking at Figure 1, we can see that from the default state we have two different probabilities and we may end up in state a with an $80%$ probability, or state c with a $20%$ probability. At every single state, the next jump is calculated using a cumulative probability algorithm that we have used before:

       float rnd = llFrand(100);
        float cum = 0;
        integer itra=llGetListLength(state_names)-1;
        do {
            cum += llList2Float(state_chances, itra);
            if(cum >= rnd) {
                if(llList2String(sName, 0) == "default") state default;
                if(llList2String(sName, 0) == "a") state a;
                if(llList2String(sName, 0) == "b") state b;
                if(llList2String(sName, 0) == "c") state c;
            }
        } while(--itra>=0);

where every transition is chosen randomly but weighted.

We exploit the concept of states in LSL and build on it a system which allows us to implement an automata that given an input transition list will perform transitions from one state to the other. Furthermore, we extend the transition list to accept a probability index which will condition every jump from one state to the other by a certain user-defined weight.

Simplified wNFA

The example code, takes as input the list QT which gives a sequence of transitions:

"default:100", "c:20|a:80", "b:100", "c:100", "a:100", "b:100", "default:50|b:50", "a:100"

At every step, the automata consumes one element of the list and takes a decision based on that probability. For example, at the start of the program, the algorithm does the following:

It consumes the first element default:100.
It takes the next element of the list c:20|a:80.
It picks a random state, state c with a weight of $20%$ and a with a probability of $80%$ .
It transits to either a or c.
It repeats the process again for the next element till it reaches the end of the list.

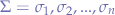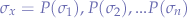That is, given an input string consisting of symbols $\Sigma = \sigma_{1}, \sigma_{2}, ..., \sigma_{n}$ , each symbol being a list of existing $\Sigma$ states where every state $\sigma_{x} = P(\sigma_{1}), P(\sigma_{2}), ... P(\sigma_{n})$ has an attached probability 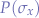$P(\sigma_{x})$ , the wNFA makes a transition to the next state $\sigma_{x+1}$ by selecting the next state randomly based on the weights of all next possible states in $\sigma_{x}$ .

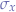Our end-states for this particular automata are either a or b. The former a is reached at the end of the list, when there are no more transitions to do and the latter b is reached before the end of the list, in case the draw default:50|b:50 results in the state b. This is particularly so, because of the LSL type NFA that does not re-enter the state_entry handler when the automata makes a transition to the same state:

state a {
  state_entry() {
    state a; //does not loop.
  }
}

There is no restriction imposed on the location of usage of the algorithm that computes the next state that the automata transits to. In the example-case provided, in order to illustrate the point, we wire the algorithm directly inside the state_entry event handler. However, one could use the algorithm whenever we would want a transition to the next state.

wnna.lsl

//////////////////////////////////////////////////////////
//   (C) Wizardry and Steamworks 2011, license: GPLv3   //
// License at: http://www.gnu.org/licenses/gpl.html     //
//////////////////////////////////////////////////////////
 
 
list QT = [ "default:100", "c:20|a:80", "b:100", "c:100", "a:100", "b:100", "default:50|b:50", "a:100" ];
 
// A quicksort, providing a stable map between two sets of elements.
list dualQuicksort(list a, list b) {
 
    if(llGetListLength(a) <= 1) return a+b;
 
    float pivot_a = llList2Float(a, llGetListLength(a)/2);
    string pivot_b = llList2String(b, llGetListLength(b)/2);
 
    a = llDeleteSubList(a, llGetListLength(a)/2, llGetListLength(a)/2);
    b = llDeleteSubList(b, llGetListLength(b)/2, llGetListLength(b)/2);
 
    list less = [];
    list less_b = [];
    list more = [];
    list more_b = [];
 
    integer i = 0;
    do {
        if(llList2Float(a, i) > pivot_a) 
        {
            less += llList2List(a, i, i);
            less_b += llList2List(b, i, i);
        }
        else
        {
            more += llList2List(a, i, i);
            more_b += llList2List(b, i, i);
        }
    } while(++i<llGetListLength(a)*2);
 
    return dualQuicksort(less, less_b) + [ pivot_a ] + [ pivot_b ] + dualQuicksort(more, more_b);
}
 
default
{
    state_entry()
    {
        llOwnerSay("state: default");
        QT = llDeleteSubList(QT, 0, 0);
        list P = llParseString2List(llList2String(QT, 0), [":", "|"], []);
        list sName = llList2ListStrided(llDeleteSubList(P, 0, 0), 0, llGetListLength(P)-1, 2);
        list sChance = llList2ListStrided(P, 0, llGetListLength(P)-1, 2);
        list sQT = dualQuicksort(sName, sChance);
        sName = llList2ListStrided(llDeleteSubList(sQT, 0, 0), 0, llGetListLength(sQT)-1, 2);
        sChance = llList2ListStrided(sQT, 0, llGetListLength(sQT)-1, 2);
        float rnd = llFrand(100);
        float cum = 0;
        integer itra=llGetListLength(sName)-1;
        do {
            cum += llList2Float(sChance, itra);
            if(cum >= rnd) {
                if(llList2String(sName, 0) == "default") state default;
                if(llList2String(sName, 0) == "a") state a;
                if(llList2String(sName, 0) == "b") state b;
                if(llList2String(sName, 0) == "c") state c;
            }
        } while(--itra>=0);
    }
}
 
state a
{
    state_entry()
    {
        llOwnerSay("state: a");
        QT = llDeleteSubList(QT, 0, 0);
        list P = llParseString2List(llList2String(QT, 0), [":", "|"], []);
        list sName = llList2ListStrided(llDeleteSubList(P, 0, 0), 0, llGetListLength(P)-1, 2);
        list sChance = llList2ListStrided(P, 0, llGetListLength(P)-1, 2);
        list sQT = dualQuicksort(sName, sChance);
        sName = llList2ListStrided(llDeleteSubList(sQT, 0, 0), 0, llGetListLength(sQT)-1, 2);
        sChance = llList2ListStrided(sQT, 0, llGetListLength(sQT)-1, 2);
        float rnd = llFrand(100);
        float cum = 0;
        integer itra=llGetListLength(sName)-1;
        do {
            cum += llList2Float(sChance, itra);
            if(cum >= rnd) {
                if(llList2String(sName, 0) == "default") state default;
                if(llList2String(sName, 0) == "a") state a;
                if(llList2String(sName, 0) == "b") state b;
                if(llList2String(sName, 0) == "c") state c;
            }
        } while(--itra>=0);
    }
}
 
state b
{
    state_entry() 
    {
        llOwnerSay("state: b");
        QT = llDeleteSubList(QT, 0, 0);
        list P = llParseString2List(llList2String(QT, 0), [":", "|"], []);
        list sName = llList2ListStrided(llDeleteSubList(P, 0, 0), 0, llGetListLength(P)-1, 2);
        list sChance = llList2ListStrided(P, 0, llGetListLength(P)-1, 2);
        list sQT = dualQuicksort(sName, sChance);
        sName = llList2ListStrided(llDeleteSubList(sQT, 0, 0), 0, llGetListLength(sQT)-1, 2);
        sChance = llList2ListStrided(sQT, 0, llGetListLength(sQT)-1, 2);
        float rnd = llFrand(100);
        float cum = 0;
        integer itra=llGetListLength(sName)-1;
        do {
            cum += llList2Float(sChance, itra);
            if(cum >= rnd) {
                if(llList2String(sName, 0) == "default") state default;
                if(llList2String(sName, 0) == "a") state a;
                if(llList2String(sName, 0) == "b") state b;
                if(llList2String(sName, 0) == "c") state c;
            }
        } while(--itra>=0);
    }
}
 
state c
{
    state_entry()
    {
        llOwnerSay("state: c");
        QT = llDeleteSubList(QT, 0, 0);
        list P = llParseString2List(llList2String(QT, 0), [":", "|"], []);
        list sName = llList2ListStrided(llDeleteSubList(P, 0, 0), 0, llGetListLength(P)-1, 2);
        list sChance = llList2ListStrided(P, 0, llGetListLength(P)-1, 2);
        list sQT = dualQuicksort(sName, sChance);
        sName = llList2ListStrided(llDeleteSubList(sQT, 0, 0), 0, llGetListLength(sQT)-1, 2);
        sChance = llList2ListStrided(sQT, 0, llGetListLength(sQT)-1, 2);
        float rnd = llFrand(100);
        float cum = 0;
        integer itra=llGetListLength(sName)-1;
        do {
            cum += llList2Float(sChance, itra);
            if(cum >= rnd) {
                if(llList2String(sName, 0) == "default") state default;
                if(llList2String(sName, 0) == "a") state a;
                if(llList2String(sName, 0) == "b") state b;
                if(llList2String(sName, 0) == "c") state c;
            }
        } while(--itra>=0);
    }
}

Weighted Non-Deterministic Non-Finite Automata (wNNA)

An extension of the wNFA is the Weighted Non-Deterministic Non-Finite Automata (wNNA) which has no final (accepting) states ( $F=\Phi$ ). One good example of a wNNA can be seen in Figure 1., the concept being used to create the great_wanderer.

$\begin{tikzpicture}[->,>=stealth',shorten >=1pt,auto,node distance=2.8cm, semithick] \tikzstyle{every state}=[fill=red,draw=none,text=white] \node (z) at (6,2) {$z$}; \node (x) at (7,-2) {$x$}; \node (y) at (2,2.5) {$y$}; % z \draw [color=blue,dashed] (-2,-6) -- (z); % x \draw [color=orange,dashed] (-3,-2) -- (x); % y \draw [color=green,dashed] (2,-7) -- (y); \node[initial,state] (A) {$default$}; \node[state] (B) [below right of=A] {$compute$}; \node[state] (C) [above of=B] {$up$}; \node[state] (D) [above right of=B] {$forward$}; \node[state] (E) [right of=B] {$right$}; \node[state] (F) [below of=B] {$down$}; \node[state] (G) [below left of=B] {$backward$}; \node[state] (H) [left of=B] {$left$}; \path (A) edge node {1} (B) (B) edge node {$p_{u}$} (C) (C) edge node {1} (B) (B) edge node {$p_{f}$} (D) (D) edge node {1} (B) (B) edge node {$p_{r}$} (E) (E) edge node {1} (B) (B) edge node {$p_{d}$} (F) (F) edge node {1} (B) (B) edge node {$p_{b}$} (G) (G) edge node {1} (B) (B) edge node {$p_{l}$} (H) (H) edge node {1} (B); \end{tikzpicture}$

As shown in Figure 1., the Great Wanderer uses the following states to navigate an enclosed space:

State	Description
default	this is the initial state.
forward	move the great wanderer forward.
backward	move the great wanderer backward.
left	move the great wanderer left.
right	move the great wanderer right.
up	move the great wanderer up.
down	move the great wanderer down.
compute	reserved for event protection.

The difference from our classic wNFA is that we do not consume states. Instead, they are re-used again, depending on the changes in probabilities for every movement: forward, backward, left, right, up and down. That makes it a Weighted Non-Deterministic Non-Finite Automata (wNNA) rather, since the Great Wanderer never stops moving and hence never ends up in an end-state. This is on purpose because the Great Wanderer is not meant to stop moving at any point.

It is, of course, feasible to convert a wNNA to a wNFA, simply by aborting or by adding an end-state if the wNNA may be extended.

Formally, a wNNA is a reduction of a wNFA where the set of final (accepting) states is empty (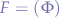 $F=( \Phi )$ ). An extra condition is that all the probabilities have to add up to the same value at every transition of the automata:

$P(t) = p_{f} + p_{b} + p_{l} + p_{r} + p_{u} + p_{d} = const.$

In other words, 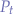$P_{t}$ must remain constant, in time, for all transitions of the wNNA (see Figure 1.). In this script, we have chosen probabilities in the range 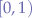$[0,1)$ for convenience.

Time-Based Automata

A different way of commuting between states would be to measure the time that it takes to execute a certain code-segment. For example, the outfit locker presents a way to exploit time in order to determine the execution flow of a program by approximating how much time each branch takes to execute.

$\begin{tikzpicture}[->,>=stealth',shorten >=1pt,auto,node distance=2.8cm, semithick] \tikzstyle{every state}=[fill=red,draw=none,text=white] \node[initial,state] (A) {$default:t \approx 1$}; \node[state] (B) [right of=A] {$b:t \approx 5$}; \node[state] (C) [above right of=B] {$c:t \approx 10$}; \node[state] (D) [below right of=B] {$d:t \approx 200$}; \node (1) at (3,2) {$(1)$}; \node (2) at (3,-2) {$(2)$}; \path (A) edge (B) (B) edge (C) (B) edge (D); \draw (C) to [out=100,in=50] (A); \draw (D) to [out=-100,in=-50] (A); \end{tikzpicture}$

Given the automata above, the only possible transitions are:

default→b→c→default
default→b→d→default

by following either the upper or the lower branch.

in case the first branch (1) is chosen, then the approximate time taken would be 16s.
in case the second branch (2) is chosen, then the approximate time taken would be 216s.

If a global timer can be set and reset in state 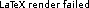$default$ (this is done in LSL with llGetAndResetTime), when switching back from either branch into the state $default$ , we can measure the time and decide whether path (1) or path (2) was taken.

Table of Contents

Introduction

NFA

Probabilistic Automata

Simplified wNFA

Weighted Non-Deterministic Non-Finite Automata (wNNA)

Time-Based Automata