Table of Contents
About
Using Second Life's physics, it is possible to simulate the scattering of particles as well as calculate energy transfers based on kinetic energy. This is possible since Second Life is able to abstracts away from friction and gravity.
Overview
Setup
The setup consists of a Cannon (@) that shoots small primitives onto a deflector. We eliminate the rotation capabilities of the small primitive using llSetStatus in order to obtain just half of the deflection angle and to eliminate other errors.
+ Detectors
+ +
|
\ / 45 deg.
|
|
| molecule
Collimator --p--
|
|
|
@ Cannon
The particles then travel on a trajectory perpendicular to the deflector and through the Collimator. In particle physics, the Collimator is used to filter out bad trajectories and to let through only direct, focused beams (pretty much like a laser works or how the Rose of Jericho is taken care of). In Second Life, however, we do not have the capabilities of the real world, such as light speed, so that the Collimator is used only to protect the deflector from reflecting particles.
After the Collimator, one or several primitives are disposed geometrically so that the small primitive shot by the Cannon collides with them. Based on that geometry, the Detectors are positioned so that they measure the impact velocity (and thus the energy transferred, based on the mass of the particles).
Cannon
The cannon or particle beam emitter is a recycled version of the artillery cannon. One of the difficulties is that the artillery cannon is under the influence of Newtonian laws, whereas a particle beam emitter propels particles at speeds that exceed Newtonian laws and are closer to relativistic laws.
This can be observed by the fact that the primitives emitted by the cannon have a downward drift - which is due to the fact that the primitives are launched from the cannon by impulse rather than a constant accelerating force (such as the one given by llSetForce).
The consequence is that the cluster of particles in front of the detectors will not be impacted in the linear direction of traveling beam of primitives through the Collimator. Instead, the traveling primitives will additionally have a downward motion which may complicate the calculations.
The cannon, in this case functions as a particle accelerator with variable speed which allows us to accelerate particles to different speeds and thus obtain different energies given the formula for kinetic energy:
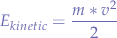
By changing the mass of particle primitives and the velocity at which they are accelerated we can obtain varying energies - again, this is bounded because too high speeds will break the simulation. There is a way to vary the mass without increasing the size of the particle. For example, newer viewers have a Density parameter that can be set per primitive.
We use the density formula:
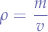
and extract the mass  :
:
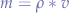
Since we do not increase the size, the volume  remains constant but we can increase or decrease the density
remains constant but we can increase or decrease the density  in order to get larger, respectively smaller masses for particles.
in order to get larger, respectively smaller masses for particles.
Newer viewers are also able to directly set the gravity as a coefficient between ![Math $[-1,1]$](/lib/exe/fetch.php?media=wiki:latex:/img699628c77c65481a123e3649944c0d51.png) , where:
, where:
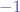 denotes downward acceleration,
denotes downward acceleration,  denotes upward acceleration and
denotes upward acceleration and  represents no gravitational influence.
represents no gravitational influence.
The speed at which primitives are accelerated can vary but at extreme speeds, the simulator is not able to sense collisions, such that the deflector does not even bounce the particle back on the desired trajectory.
Target Selection
In particle physics, the target is usually a thin plate of some material. That material contains molecules that get split by colliding particles from the accelerator (in our case, we use the cannon script provided below).
material
+--+ +---+
| | - - | o |
+--+ - - | o | accelerated
- - | o |<-------
+--+ - - | o | particles
| | - - | o |
+--+ +---+
detectors
In Second Life, we have the convenience of being able to create molecules at a larger scale and even specify their geometric distribution.
Based on the molecule geometries (for instance, the disposition of atoms), we can calculate exactly in what direction the atom will be propelled when an accelerated particle collides with the molecule.
Splitting Molecules
A dipole molecule is a molecule that consists of three binding atoms, for example an 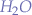 molecule:
molecule:
![LaTeX
\begin{tikzpicture}
% particles
\node [circle,minimum size=20mm] at (-1,0) [draw] (alpha) [black,fill,text=white] {$O$};
\node [circle,minimum size=20mm] at (1,0) [draw] (beta) [black,fill,text=white] {$O$};
% lines
\draw [red,|-|,thick] (-2,-1.5) -- (0,-1.5) node[anchor=north] {$120.74\mu m$} -- (2,-1.5);
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/img63d2ed238e8db03d262d81934e0f7356.png)
In order to split the molecule into two  atoms, we accelerate a particle to a certain speed and collide with the
atoms, we accelerate a particle to a certain speed and collide with the  molecule. The speed would depend on the binding force between the two atoms. In Second Life's case, it seems that masses of physical objects, do attract each other as they would in reality. For example, two spheres containing the following script:
molecule. The speed would depend on the binding force between the two atoms. In Second Life's case, it seems that masses of physical objects, do attract each other as they would in reality. For example, two spheres containing the following script:
/////////////////////////////////////////////////////////////////////////// // Copyright (C) Wizardry and Steamworks 2013 - License: GNU GPLv3 // // Please see: http://www.gnu.org/licenses/gpl.html for legal details, // // rights of fair usage, the disclaimer and warranty conditions. // /////////////////////////////////////////////////////////////////////////// default { state_entry() { llSetStatus(STATUS_PHYSICS, TRUE); llSetForce(<0,0,9.81>*llGetMass(), FALSE); llSetText("Initial Position: " + (string)llGetPos() + "\n", <1,0,0>, 1.0); llSetTimerEvent(1); } timer() { string text = llList2String(llGetPrimitiveParams([PRIM_TEXT]), 0); list s = llParseString2List(text, ["\n"], []); llSetText(llList2String(s, 0) + "\n" + "Current: " + (string)llGetPos(), <1,0,0>, 1.0); } }
are placed separate from each other. By dragging one of the spheres closer to the other, one can notice the other sphere move, slightly in the direction of the approaching sphere.
Incidence Angle Calculations
Supposing that we have a direct impact, the geometrical disposition of particles (as well as their mass) influence the drift towards the Detectors which are placed based on the angle of incidence onto the molecule.
Dipole
For a dipole, 3 atoms in a molecule, for example,  , suppose that we have the following geometric disposition:
, suppose that we have the following geometric disposition:
![LaTeX
\begin{tikzpicture}
% grid
\draw[help lines] (-4,-4) grid (4,4);
% detectors
\node [square,rotate={30},minimum size=10mm] at (-3, {3 * sqrt(3) - sqrt(3)}) [draw] (d2) [pink,fill,text=white] {$d_{2}$};
\node [square,rotate={-30},minimum size=10mm] at (3, {3 * sqrt(3) - sqrt(3)}) [draw] (d2) [pink,fill,text=white] {$d_{2}$};
% particles
\node [circle,minimum size=20mm] at (-1,0) [draw] (alpha) [black,fill,text=white] {$p_{1}$};
\node [circle,minimum size=20mm] at (1,0) [draw] (beta) [black,fill,text=white] {$p_{2}$};
\node [circle,minimum size=20mm] at (0,{-sqrt(3)}) [draw] (hello) [red,fill,text=white] {$p$};
% forces
\draw [cyan,->,thick] (0,{-sqrt(3)}) -- (0,2) node[anchor=east] {$F_{p}$};
\draw [cyan,->,thick] (0,{-sqrt(3)}) -- (1,0) node[anchor=north west] {$F_{2}$};
\draw [cyan,->,thick] (0,{-sqrt(3)}) -- (-1,0) node[anchor=north east] {$F_{1}$};
% trajectories
\draw [orange,->,thin,dotted] (0,{-sqrt(3)}) -- (3,{3*sqrt(3)-sqrt(3)});
\draw [orange,->,thin,dotted] (0,{-sqrt(3)}) -- (-3,{3*sqrt(3)-sqrt(3)});
%\draw [orange,->,thick] (0,{-sqrt(3)}) -- (-1,0);
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/imge3af4ecfa6a6858ddac8e01bc16ab569.png)
The mobile particle is the red one, noted with  and the other two particles
and the other two particles  and
and  could belong to a dipole molecule. We need to calculate the placement and rotation of the detectors so that both particles are deflected perpendicular to the surface of the detector (although, the rotation is not necessary because Second Life primitives detect collisions regardless of where they occur on the surface of the primitive).
could belong to a dipole molecule. We need to calculate the placement and rotation of the detectors so that both particles are deflected perpendicular to the surface of the detector (although, the rotation is not necessary because Second Life primitives detect collisions regardless of where they occur on the surface of the primitive).
Detector Placement
![LaTeX
\begin{tikzpicture}
% grid
\draw[help lines] (-4,-4) grid (4,4);
% coordinates
% origin
\draw[red, line width=.1mm] (-0.1,-0.1) -- (0.1,0.1)
(0.1,-0.1) -- (-0.1,0.1);
\coordinate[label={[red]above:$O$}] (O) at (0,0);
\coordinate[label={[blue]below:$p$}] (P) at (0,{-sqrt(3)});
\coordinate[label={[blue]below:$p_{2}$}] (A) at (1,0);
\coordinate[label={[blue]below:$p_{1}$}] (B) at (-1,0);
% detectors
\node [square,rotate={-30},minimum size=10mm] at (3, {3 * sqrt(3) - sqrt(3)}) [draw] (d2) [pink,fill,text=white] {$d_{2}$};
% lines
\draw [cyan,thick,dotted] (P) -- (0,2);
\draw [cyan,thick] (P) -- (A);
\draw [cyan,thick] (P) -- (B);
\draw [red,thick,dotted] (B) -- (A);
% angles
\markangle{P}{A}{O}{7mm}{9mm}{$\beta$}{red}{west}
\markangle{P}{B}{O}{5mm}{3mm}{$\alpha$}{red}{north east}
% trajectories
\draw [orange,thick,dotted] (P) -- (3, {3 * sqrt(3) - sqrt(3)});
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/img7c5f51e69eda47320aa743cc348621d5.png)
In the triangle formed by  , we know that
, we know that 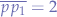 and that
and that 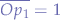 . Now, we know that
. Now, we know that 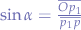 and we obtain that
and we obtain that  meaning that
meaning that  .
.
Consider the triangle formed by  , since it has a right-angle in
, since it has a right-angle in  , we can write the following relation:
, we can write the following relation:
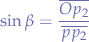
And since  is the bisectrice of the triangle
is the bisectrice of the triangle  starting from point
starting from point  , we know that
, we know that 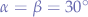 . Thus, we can write that:
. Thus, we can write that:
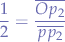
which means that 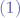
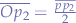 .
.
Next, we apply Pythagoras in the triangle formed by  , writing that:
, writing that:
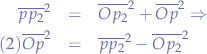
Now, we substitute 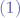 in
in 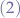 , obtaining that:
, obtaining that:
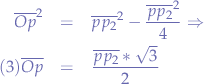
Let us sum up what we have obtained, first by using the sinus relation and then Pythagoras in triangle  :
:
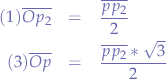
If you look at the triangle  , we now know both sides of the triangle
, we now know both sides of the triangle  (
( and
and  ) in relation to the hypothenuse
) in relation to the hypothenuse  . By doing so, we can now give values to the hypothenuse
. By doing so, we can now give values to the hypothenuse  in order to find both sides of the triangle and determine where the detector should be placed. Let us rewrite both equations and give them nicer names:
in order to find both sides of the triangle and determine where the detector should be placed. Let us rewrite both equations and give them nicer names:
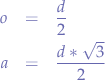
where  represents the side opposite to the angle
represents the side opposite to the angle  ,
,  represents the adjacent side to the angle
represents the adjacent side to the angle  and
and  a distance from the colliding particle
a distance from the colliding particle  .
.
Let us take an example, consider a larger triangle such that the detector is placed 6 units away from the colliding particle  . In that case, let:
. In that case, let:

If so, then we want to know the 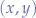 coordinates where the detector will be placed. Now, we can determine the sides of the wider triangle:
coordinates where the detector will be placed. Now, we can determine the sides of the wider triangle:
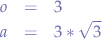
Thus, the detector 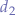 can be found at
can be found at  - we subtract
- we subtract  because that represents the distance between the particle
because that represents the distance between the particle  and the origin
and the origin  . Substituting with values, we obtain
. Substituting with values, we obtain 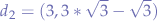 .
.
![LaTeX
\begin{tikzpicture}
% grid
\draw[help lines] (-4,-4) grid (4,4);
% coordinates
% origin
\draw[red, line width=.1mm] (-0.1,-0.1) -- (0.1,0.1)
(0.1,-0.1) -- (-0.1,0.1);
\coordinate[label={[red]above:$O$}] (O) at (0,0);
\coordinate[label={[red]above:$d_{2}$}] (D) at (3, {3 * sqrt(3) - sqrt(3)});
\draw[red, line width=.1mm] ({3-0.1}, {3 * sqrt(3) - sqrt(3)-0.1}) -- ({3+0.1}, {3 * sqrt(3) - sqrt(3)+0.1})
(3+0.1, {3 * sqrt(3) - sqrt(3)-0.1}) -- (3-0.1, {3 * sqrt(3) - sqrt(3)+0.1});
\coordinate[label={[blue]below:$p$}] (P) at (0,{-sqrt(3)});
\coordinate[label={[blue]below:$p_{2}$}] (A) at (1,0);
\coordinate[label={[blue]below:$p_{1}$}] (B) at (-1,0);
\coordinate (H) at (3,-sqrt(3));
% lines
\draw [cyan,thick,dotted] (P) -- (0,2);
\draw [cyan,thick] (P) -- (A);
\draw [cyan,thick] (P) -- (B);
\draw [red,thick,dotted] (B) -- (A);
% angles
\markangle{P}{A}{O}{7mm}{9mm}{$\beta$}{red}{west}
\markangle{P}{B}{O}{5mm}{3mm}{$\alpha$}{red}{north east}
% trajectories
\draw [orange,thick,dotted] (P) -- (3, {3 * sqrt(3) - sqrt(3)});
% helpers
\draw [cyan,thick,dotted] (3, {3 * sqrt(3) - sqrt(3)}) -- (H);
\markangle{D}{P}{H}{5mm}{3mm}{$\beta$}{red}{east}
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/imgf7710ba849dc3b8445042e4dd7d4f91c.png)
The rotation of the detector is the same as angle  . This is because if we draw a vertical line going through
. This is because if we draw a vertical line going through 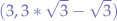 it would be parallel to the line given by
it would be parallel to the line given by  and thus the inner angles will be the same and equal to
and thus the inner angles will be the same and equal to  .
.
Breaking our First Dipole Molecule
We set-up an experiment to break up a dipole molecule, constructed of atoms  ,
,  respectively
respectively  by colliding an incident particle from the accelerator.
by colliding an incident particle from the accelerator.
![LaTeX
\begin{tikzpicture}
% grid
\draw[help lines] (-4,-4) grid (4,4);
% detectors
\node [square,minimum size=10mm] at (0, {3.5}) [draw] (d2) [pink,fill,text=white] {$d_{1}$};
\node [square,minimum size=10mm] at (-3, {3 * sqrt(3) - sqrt(3)}) [draw] (d2) [pink,fill,text=white] {$d_{2}$};
\node [square,minimum size=10mm] at (3, {3 * sqrt(3) - sqrt(3)}) [draw] (d2) [pink,fill,text=white] {$d_{3}$};
% particles
\node [circle,minimum size=20mm] at (-1,0) [draw] (alpha) [draw=grey!30,fill=grey!30,text=black] {$p_{2}$};
\node [circle,minimum size=20mm] at (1,0) [draw] (beta) [draw=grey!30,fill=grey!30,text=black] {$p_{3}$};
\node [circle,minimum size=20mm] at (0,{-sqrt(3)}) [draw] (hello) [draw=grey!30,fill=grey!30,text=black] {$p_{1}$};
% forces
\draw [>=latex,draw=blue,fill=blue,->] (0,{-sqrt(3)}) -- (0,2) node[anchor=east] {$F_{1}$};
\draw [>=latex,draw=blue,fill=blue,->] (0,{-sqrt(3)}) -- (1,0) node[anchor=north west] {$F_{3}$};
\draw [>=latex,draw=blue,fill=blue,->] (0,{-sqrt(3)}) -- (-1,0) node[anchor=north east] {$F_{2}$};
\draw [>=latex,draw=red,fill=red,->] (0,-4) -- (0,-3) node[anchor=north east] {$F_{impact}$};
% trajectories
\draw [orange,->,thin,dotted] (0,{-sqrt(3)}) -- (3,{3*sqrt(3)-sqrt(3)});
\draw [orange,->,thin,dotted] (0,{-sqrt(3)}) -- (-3,{3*sqrt(3)-sqrt(3)});
\draw [orange,->,thin,dotted] (0,{-sqrt(3)}) -- (0,3.5);
%\draw [orange,->,thick] (0,{-sqrt(3)}) -- (-1,0);
\end{tikzpicture}](/lib/exe/fetch.php?media=wiki:latex:/img9e34d2543168ce2d184a64af92310545.png)
Work-Energy Principle
Given Netwon's third and second laws, we write that:
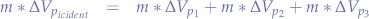
where  represents particle emitted by the cannon and,
represents particle emitted by the cannon and,  ,
,  and
and  represent the particles making up the molecule.
represent the particles making up the molecule.
In our chosen example, all the particles, including the incident particle have the same mass, we can rewrite the equation such that:
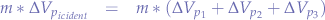
and hence simplify the masses:
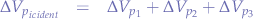
We know that  is an acceleration
is an acceleration  but the particle simulator fires the incident particle at a constant velocity, and thus the equation reduces to:
but the particle simulator fires the incident particle at a constant velocity, and thus the equation reduces to:
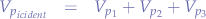
which should be satisfied if the particle scatter simulator works correctly.
First Test Case
In the video test case, we gather the following data from the cannon and the scintillators:
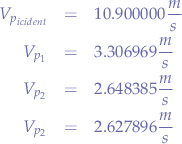
subtracting we obtain the difference  with an error of
with an error of  (disappointingly large, but good considering that the detectors were not accurately placed).
(disappointingly large, but good considering that the detectors were not accurately placed).
Second Test Case
Trying again, we gather the following data from the cannon and the scintillators:
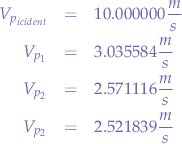
subtracting we obtain the difference  with an error of
with an error of  (a little better).
(a little better).
Index
For the contact, copyright, license, warranty and privacy terms for the usage of this website please see the contact, license, privacy, copyright.



