Table of Contents
Shortnote
The following is a collection of functions that process matrices in LSL.
Most functions are recursive and modularly compute some matrix operation - this is purposefully done so in order to be able to dismantle and reuse individual components of the code.
Most functions used by the calculators have quadratic complexity. There may be faster numerical methods to calculate the determinant and obtain the inverse of a matrix however this implementation seeks to emulate a pen and paper solution using Laplace - for example, one could use the code to display solutions in real-time by moving the primitive or using particle effects to show the actual numbers being computed.
Video
Determinant
Computing the determinant of a matrix is performed by following a given row and computing the value of the adjugates. For example, suppose we have a  matrix
matrix  of the form:
of the form:
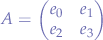
that would mean that:
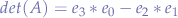
For larger matrices, supposing that  represents a sub-matrix of
represents a sub-matrix of  , its determinant has to be computed. This is performed recursively by traversing a matrix row and then calling
, its determinant has to be computed. This is performed recursively by traversing a matrix row and then calling wasDeterminant on any sub-matrix.
For a larger matrix, such as:

the element must be multiplied with the value of the sub-determinant while minding the alternation of the signs. In this case:
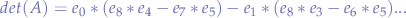
Adjugate
The adjugate step consists in finding the cofactor (determinants) of every element in the matrix and replacing the original value with the cofactor of the sub-matrix. For example, for a matrix  :
:
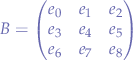
One would take each element, ignore the row and column it appears in and compute the determinant of the sub-matrix  . For example, in this particular case, the element
. For example, in this particular case, the element 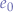 will be replaced with the value of the determinant:
will be replaced with the value of the determinant:
![Equation $$
B_{e_{0}} =
\left[ \begin{matrix}
e_{4} & e_{5} \\
e_{7} & e_{8}
\end{matrix} \right]
$$](/lib/exe/fetch.php?media=wiki:latex:/img635c01f828e801d5991970549b2ca2bc.png)
The signs alternate on rows and columns, for example, the cofactor of the second element 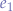 will have a negative sign:
will have a negative sign:
![Equation $$
B_{e_{1}} = -
\left[ \begin{matrix}
e_{3} & e_{5} \\
e_{6} & e_{8} \\
\end{matrix} \right]
$$](/lib/exe/fetch.php?media=wiki:latex:/imgb11ee0b1dad6ecd484bc73098b1d496d.png)
The same applies to the cofactor of element  , that will have a negative sign as well:
, that will have a negative sign as well:
![Equation $$
B_{e_{3}} = -
\left[ \begin{matrix}
e_{1} & e_{2} \\
e_{7} & e_{8}
\end{matrix} \right]
$$](/lib/exe/fetch.php?media=wiki:latex:/imgd759c31dd3b85777980535037bd0ed20.png)
By going through every element of the matrix and replacing each element with value of the determinants of the sub-matrix (also called the co-factor), we obtain a new matrix that has to finally be transposed in order to finally obtain the adjugate of the matrix.
One can note that at the time of writing the cofactor function does not bother with applying signs to the values - this is performed later on in by the adjugate or determinant functions.
Scalar Product
For a multiplication between a scalar  and a matrix
and a matrix  so that
so that 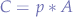 :
:
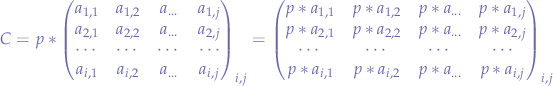
we multiply the scalar  with every element in
with every element in  in order to obtain the resulting matrix
in order to obtain the resulting matrix  .
.
Dot Product
In order to multiply two matrixes, the number of columns of the first matrix  has to be equal to the number of rows of the second matrix
has to be equal to the number of rows of the second matrix  .
.
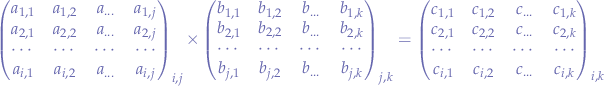
in this case, we have  and
and  with
with  . For every element in
. For every element in  we multiply elements from the rows of
we multiply elements from the rows of  with elements from the column of
with elements from the column of  and add them up to obtain the elements in
and add them up to obtain the elements in  .
.
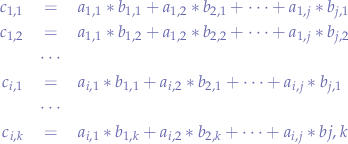
Programming Notes

Although the operations are straight-forward, writing a program to perform them is non-trivial because it implies deep recursion for very large matrices - especially when computing the adjugate. This implies quadratic time, and even more so since every element will have to be handled and every sub-matrix will have to be processed. Thus, very large matrices will take a long time to compute due to the restrictions of LSL. Another difficulty is that LSL does not have an equivalent of multi-dimensional arrays and a matrix can be expressed at best as a flattened list. Given sufficient time, the implementation succeeds at some point and manages to compute the inverse for matrices of large dimensions.
Index
For the contact, copyright, license, warranty and privacy terms for the usage of this website please see the contact, license, privacy, copyright.


