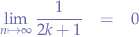Table of Contents
Taylor Series
The Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivates at a single point. Its utility could be to graphically represent functions by selecting a sufficient number of terms and thus decreasing the error gradually.

or, in expanded form:
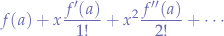
For the case  , the series is a particular case of the Taylor Series, called the Maclaurin series.
, the series is a particular case of the Taylor Series, called the Maclaurin series.
Example: Maclaurin for Cosine Function
Find the Maclaurin expansion for  :
:
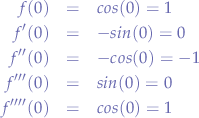
which is a repeating pattern.
Now we expand the coefficients:
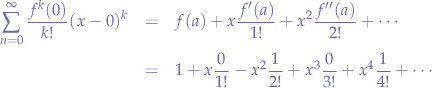
observing that certain nominators contain  and can be reduced, we obtain the final formula for
and can be reduced, we obtain the final formula for  :
:
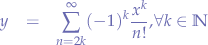
Convergence Test
Using the alternating series procedure, the series converges because:
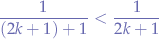
and